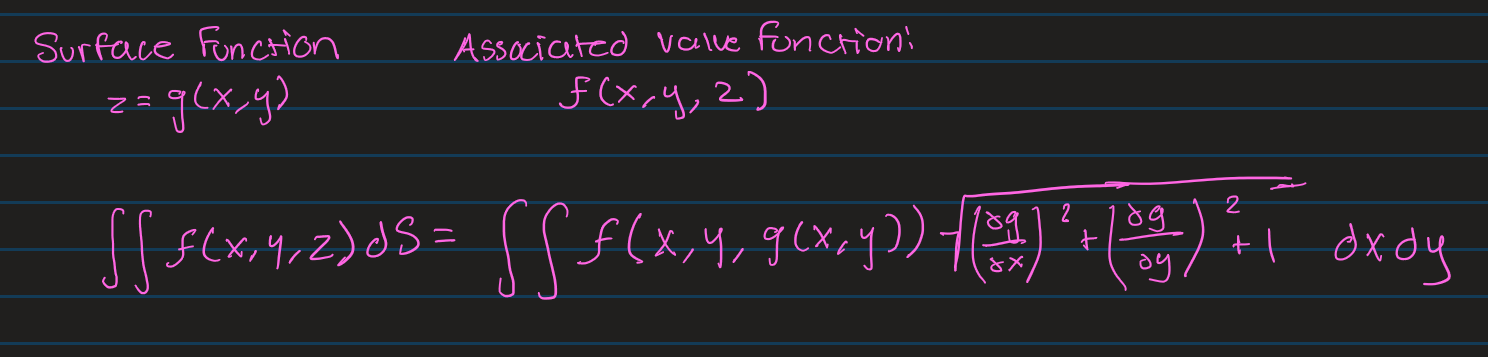Calculus 3

Unit Vector

Vector Divided by the Magnitude of the Vector. Magnitude of the unit vector is 1.

Terminal Point of a Vector

The ending point of a vector.

Vector Equation of Two Points

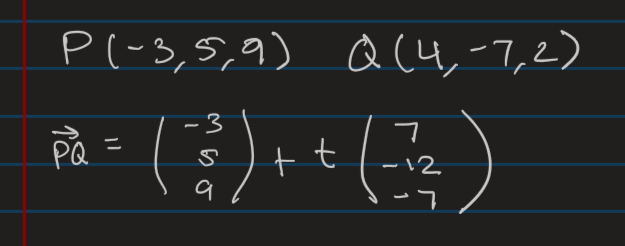
Obtaining Point and Direction Vector from Parametric Equations

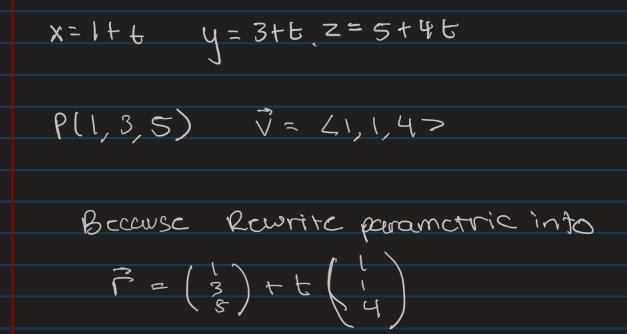
Area of a Parallelogram (Magnitude of Cross Product)

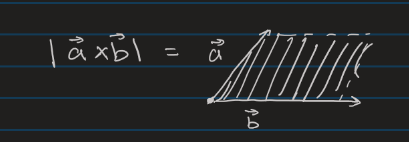
Cross Product

Outputs Normal Vector

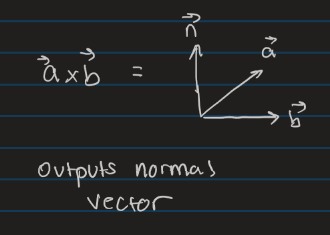
Formula For Shortest Distance from any Point to a line

Idea is to create a parallelogram where you can compute the area from a cross product. Then you can set it equal to the formula of base times height. Then divide by magnitude of the base vector to find height.

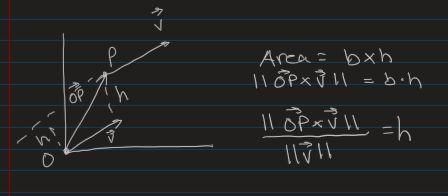
Shortest Distance from Origin/Any Point to a line 

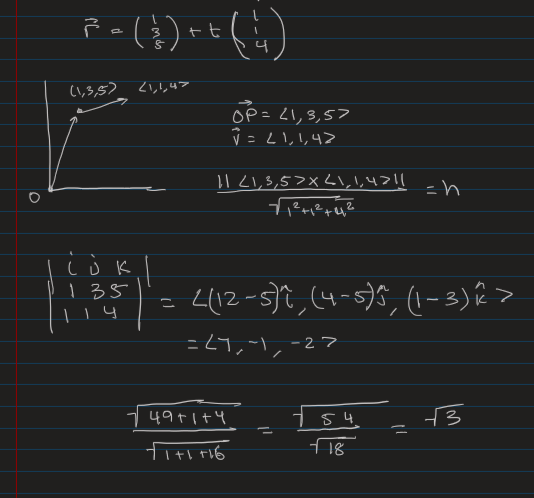
Writing the Plane Equation when Given Point and Normal Vector

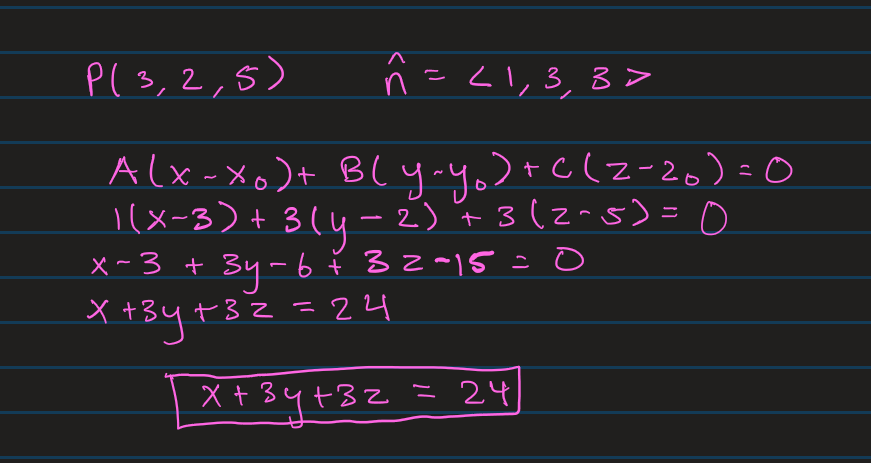
Parametric Form of a Plane

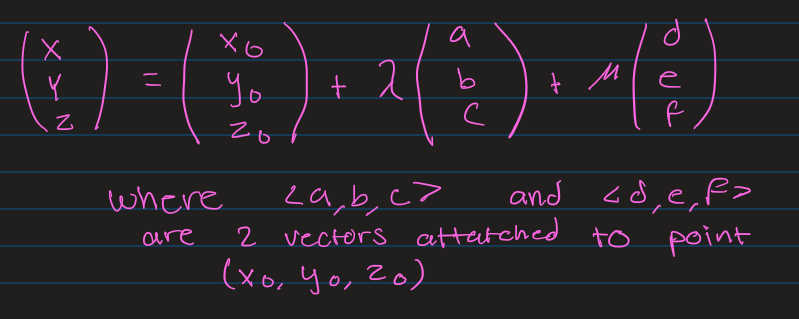
Standard/Point Form of a Plane

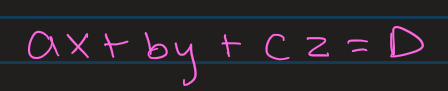
Finding Tangent Vector to a Vector Function

Take derivative of original function.

Alternate question is that they give you a point on the curve instead of the t value. Then you must solve for the t value based off the point value they give. Then do the same steps using the deducted t value.

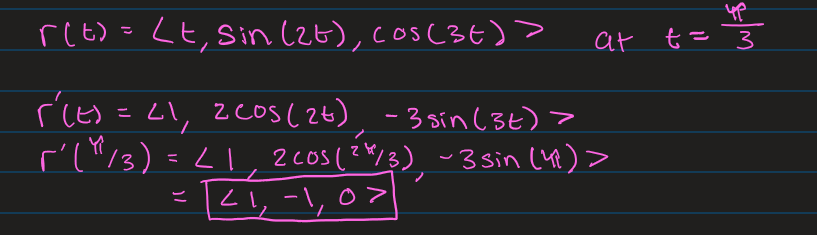
Limits of Vector Functions/Parametric Functions

You take the limit of each of the components and if each component exists and equals some constant value then the whole limit exists.

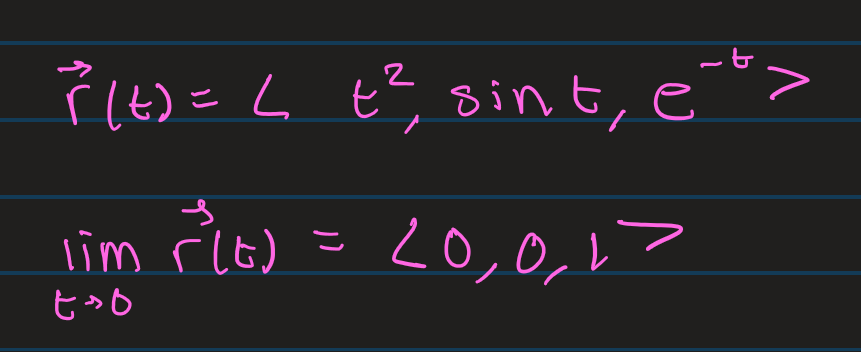
Limits of Multivariable Functions

This is the one where you have to use Squeeze Theorem or show that it is the same from multiple different lines/approaches.

Example of Taking the Limit With Difference of Squares Manipulation

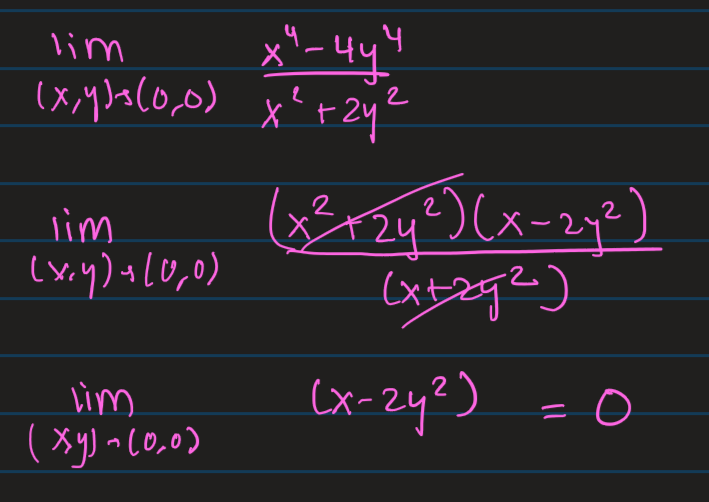
Example of Taking the Limit by Multiplying by Conjugate to get rid of Square Root on Bottom

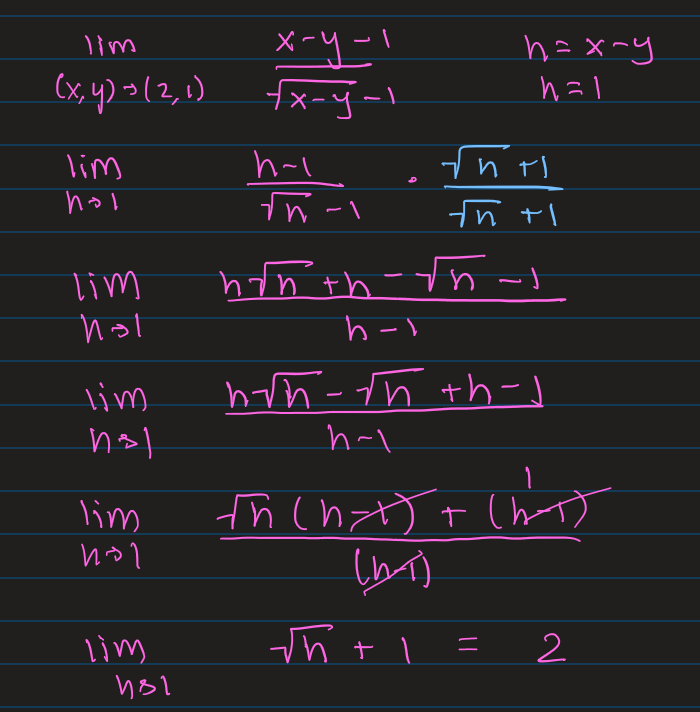
Using Squeeze Theorem in Polar Coordinates

You can treat cos theta and sin theta as 1 since they at their max they are bounded by 1.

If an r exists in the simplified expression then usually it is 0. If there is only theta in the expression then it is DNE. If it is a constant (r and theta cancel out) then it is just equal to that constant.

Example of Taking the Limit by Approaching the Function from different directions

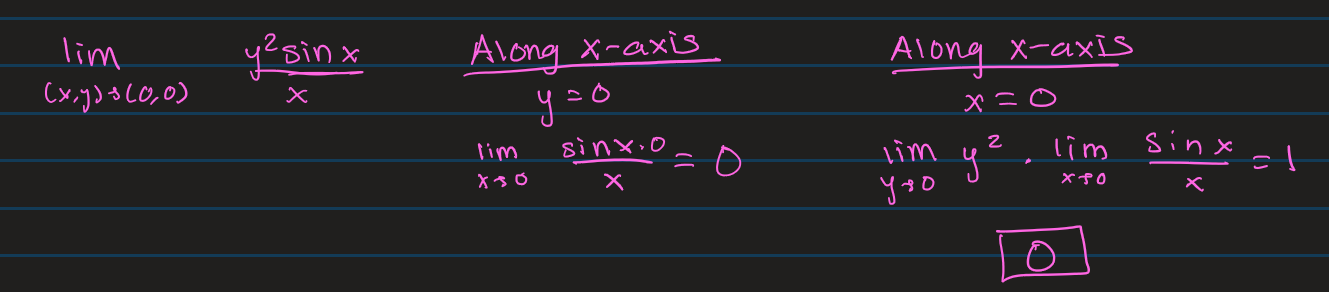
Derivative of Cross Product and Dot Product

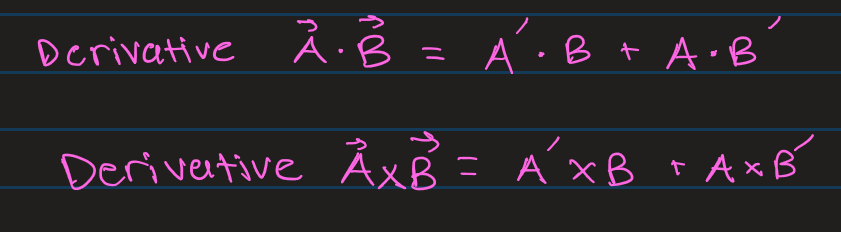
Taking a derivative of a multivariable function

When you take a derivative of a multivariable function you get partial derivatives for each. This partial derivatives can be used to construct the gradient vector which is also a function. If this vector function is conservative you can integrate over this function to get back the original function.

Arc Length Formula

Think of integrating over the velocity function. Pretend original function is position and then you take the derivative and find velocity and than take the magnitude and integrate.

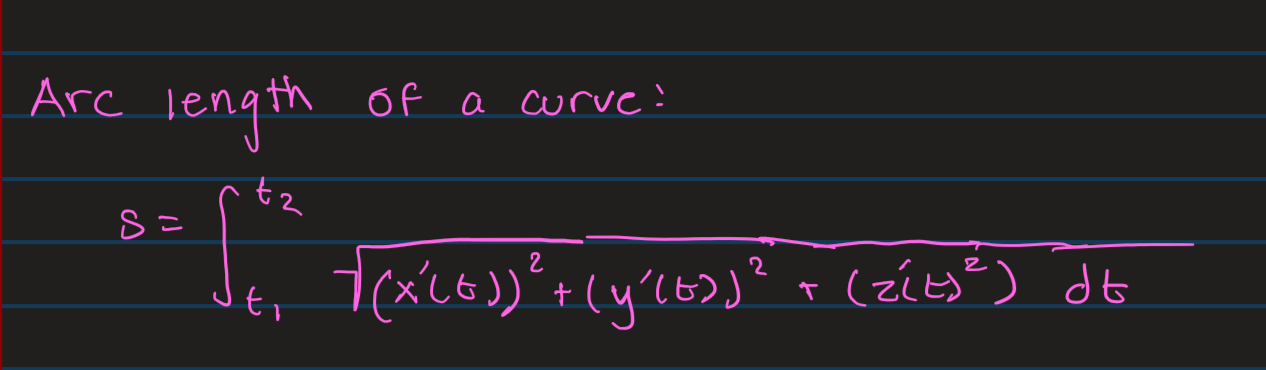
Arc Length Parameterization

Process of finding the Arc Length formula in terms of t. Then resolving so that t = something times s. Then re substitute the t in the original function to create a new parameter of s.

In Which Direction does the Gradient Point for a Surface?

The gradient point in the direction in steepest ascent. Direction up hill.

Partial Derivative (Intuition Behind Directional Derivative)

Partial Derivative is basically the same as a directional derivative but it is in the direction of the unit vectors of i, j, k or the axes. It represents the rate at which the function changes as you traverse those axes when you keep the other variables constant.

Directional Derivative

Partial Derivative but instead of pointed in direction of axes it is in the direction of some arbitrary vector we want. To calculate:

Dot the Gradient Vector with the Unit Vector for the specific direction.

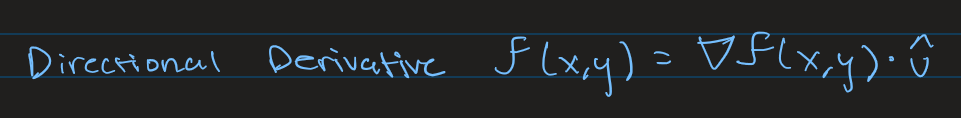
Explicit Surface vs Implicit Surface

2 ways to represent a function. You can convert from explicit to implicit, but not always convert from implicit to explicit. It can be converted back and forth if it remains one to one.

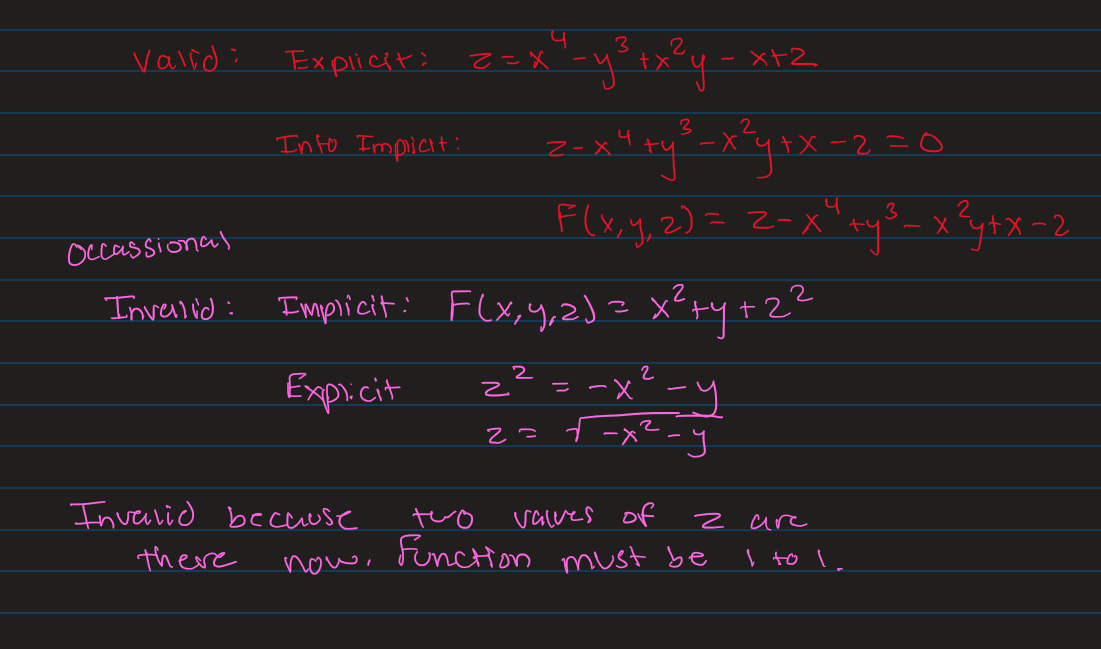
Weird Example of Using the Plugging Stuff into Limit and Solving

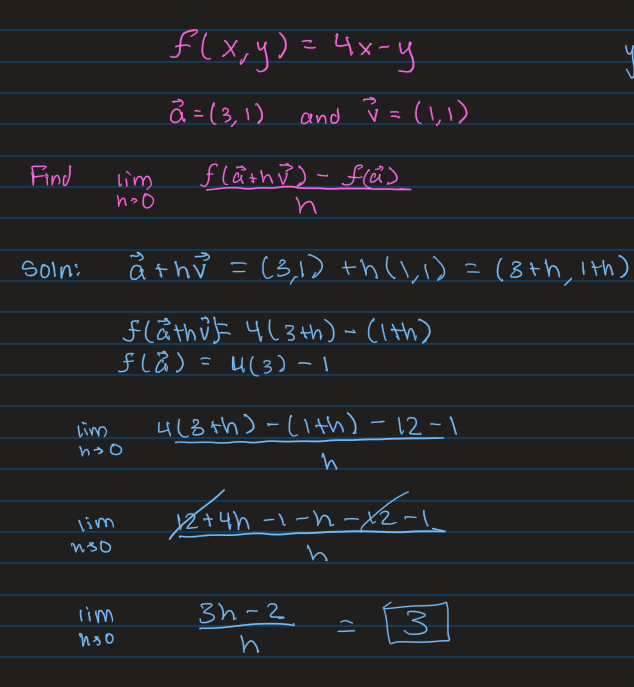
Divergence

Divergence is basically if you pick a point within a vector field how much vectors come into vs leave. If a point has positive divergence more particles travel leave a region in a vector field than into. If a point has negative divergence than more particles travel into a region than leave it.

Divergence Formula

This can be expanded into 3 dimensions as well.

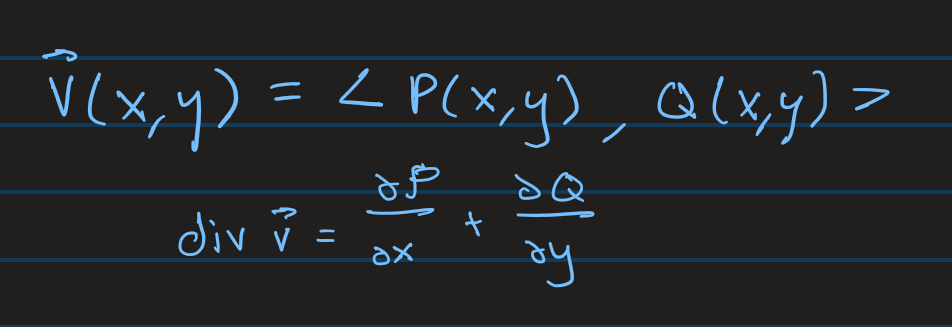
Curl

The amount of curl the vectors within a region would give a particle. Positive curl means the counter clockwise direction and negative curl means the clockwise direction.

2D Curl

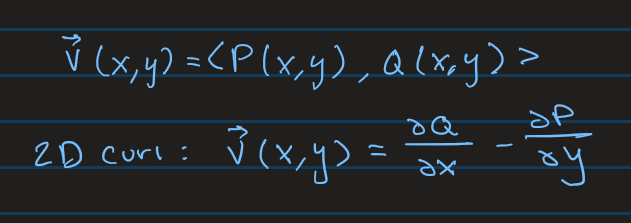
3D Curl

Simple Chain Rule Example

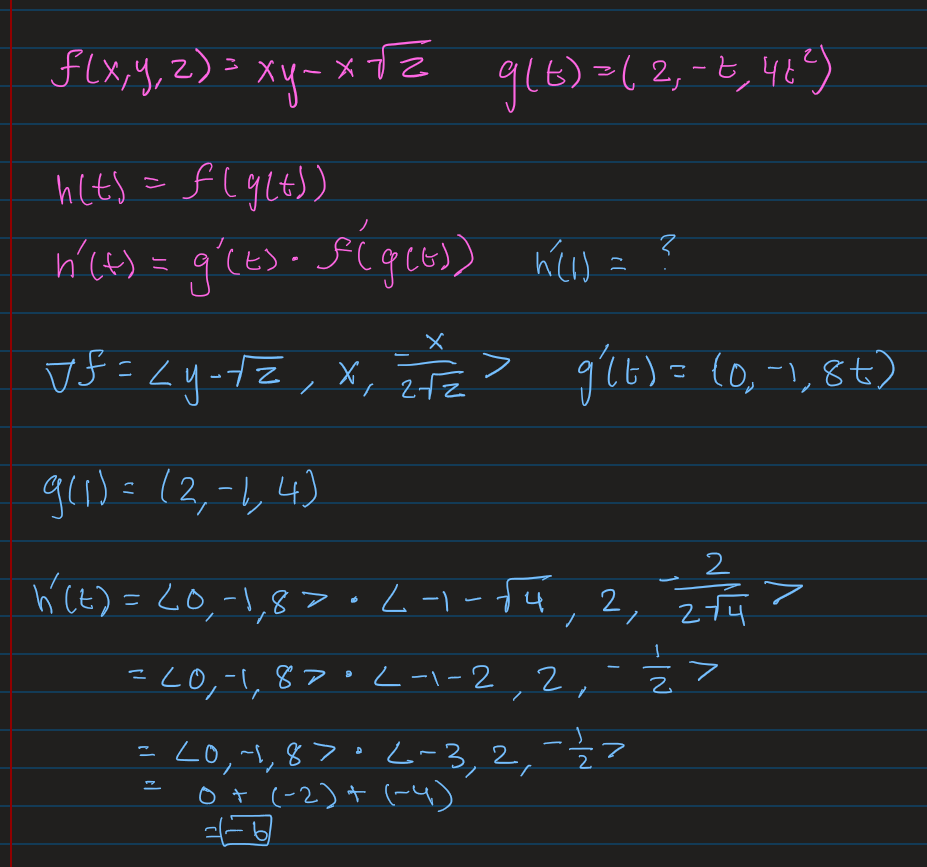
Tangent Planes

For Tangent Planes REMEMBER YOU ALWAYS NEED A Z POINT. Therefore if you aren’t given one then you must solve for it by plugging in x and y.

This is an example of an explicit function. The idea is to always write it implicitly to form your gradient vector.

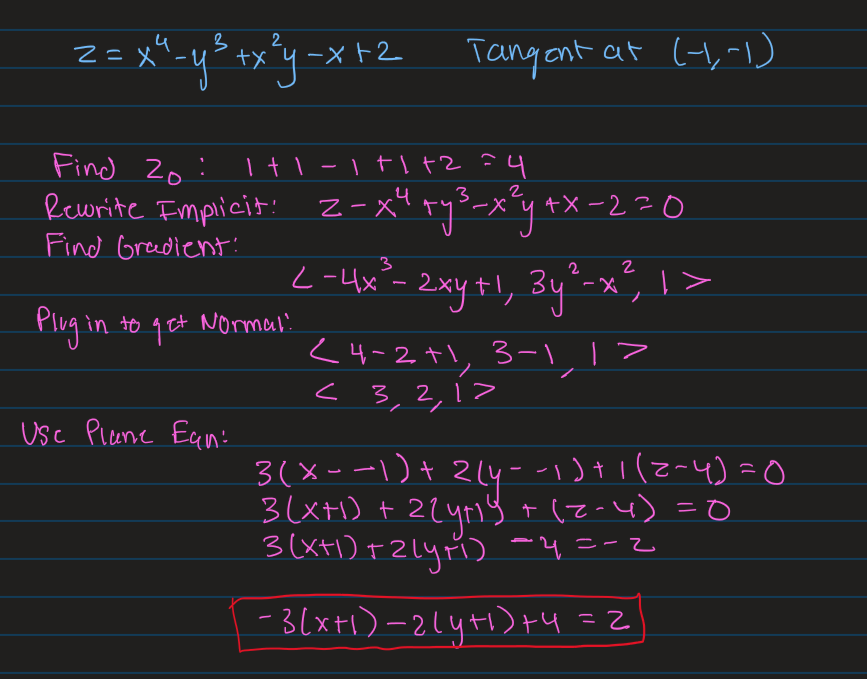
What is a line integral

A line integral is like a single-variable integral, except instead of integrating along a straight line on one axis, you integrate along a curve in space.

Interesting Example of Rewriting Bounds

Interesting Example of Rewriting Circular Bounds

Example of Rewriting Bounds for Intuition

The general idea is to realize which direction you are summing up values. Also graph the bounds to help visualize.

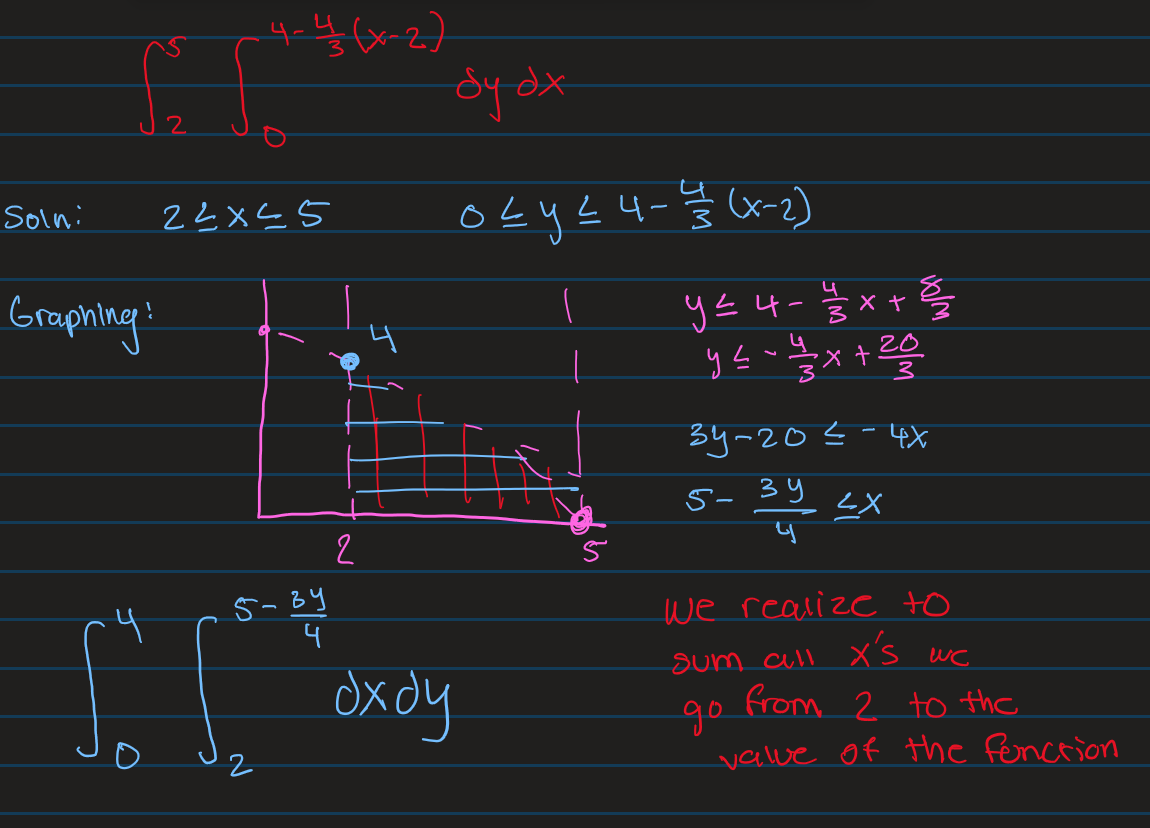
Surface Integral Coneptually

Analogous to the Line Integral. We have a 3d surface, and for each small section of surface on that 3d surface (remember a surface is a 3d shell) we have some extraneous value associated that is given by another function.

For example, lets say we have the surface x²+y²+z² = 1, which is a sphere. Then we have another function G(x,y,z) = x + y + z.  This function we would point every point of the sphere and get another value pretend it is temperature.

For the surface integral we are basically trying to find the total temperature of the sphere by integrating over all the little temperature values that we get from plugging in x, y, z from our surface.

What is Surface Parameterization?

Surfaces are inherently 2-D objects that live in 3-D space. Therefore you can describe a surface using 2 variables and that is the process of parameterizing a surface. You try to represent a 3D object with 2 separate variable and make X, Y, and Z functions of those 2 variables.

r(u,v)=⟨x(u,v), y(u,v), z(u,v)⟩.

Surface Integral of a Parameterized Surface

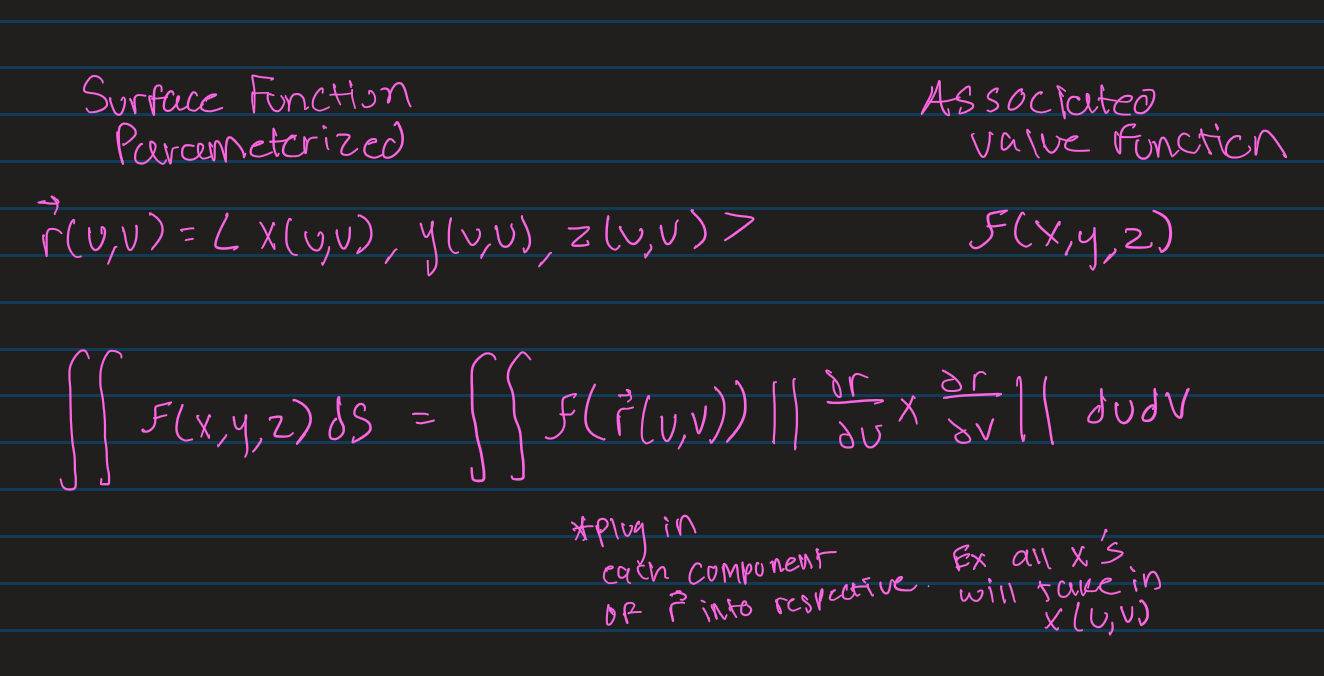
Surface Area of a Explicitly Defined Surface