Circular Motion & SHM

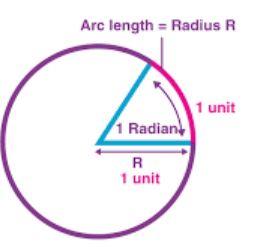
What is the definition of a radian?

The angle subtended at the centre of a circle by an arc equal in length to the radius.

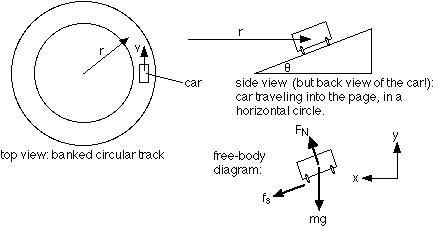
mgtan(theta) = mv²/r

What is equation to work out percentage uncertainties, given the range of data and the mean?

½ (Range) / Mean x 100

Don’t FORGET HALF

(When measuring with an instrument, the smallest scale division determines the resolution. The uncertainty is typically taken as half the smallest division because the true value could reasonably lie anywhere within ± half of that division around a reading.)

What are the equations for angular speed?

w = θ/t (object object turns through in radians)

w = v/r (v is linear velocity), r = radius

What is an equation that relates V max to frequency and Amplitude?

v = 2 pi f A (useful!!) (where 2 pi f is w)

What is meant by a forced vibration?

Oscillation due to external periodic driving force

A (REMEMBER T is 1/f!)

How can at maximum displacement for a pendulum, acceleration be maximum if the velocity is 0?

Remember, when dealing with simple harmonic motion, a is not equal to v/t. Instead, a = -w²r, which allows v to be 0 (2 pi f)

w = v/r is valid for instantaneous velocity in circular motion, not at points where the tangential velocity is zero. (when v is not equal to 0)

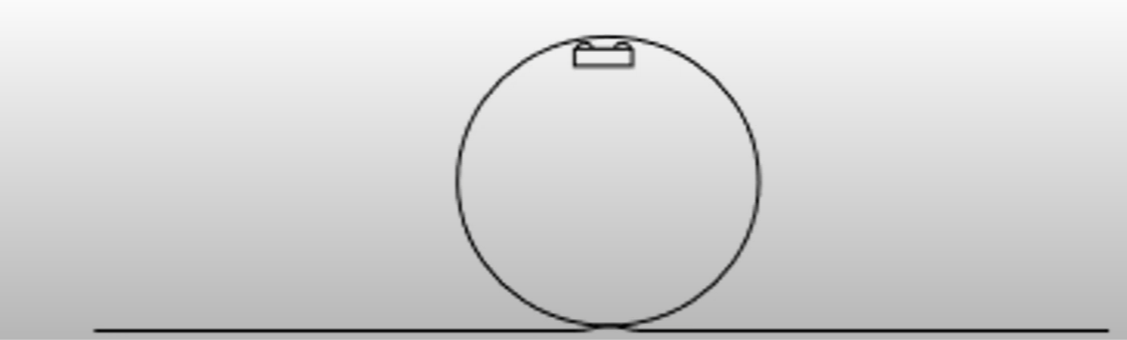
What provides the centripetal force to keep the car moving in this position?

The weight of the car.

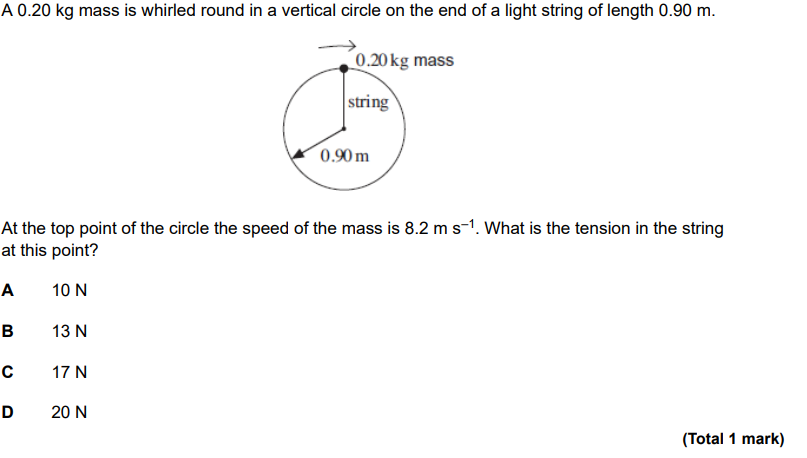
How do you find the Tension in a cable attached to a mass, moving in circular motion at the TOP of its circle?

Tension always points towards centre of circle. Draw centripetal force, weight and tension on a diagram and derive that: mv²/r = T + mg and re arrange and solve for T,

Answer is C

How to calculate the MAXIMUM and MINIMUM tension in a string connected to a mass in circular motion?

MAXIMUM = When mass is at the bottom of the circular path, mv²/r = T -mg

MINUMUM = Top of circular path, mv²/r = T +mg

Rearrange for T in both cases.

When would you include the weight of the object to calculate the tension in a string of an object undergoing circular motion?

ONLY when string is vertical. (Only for tension, NOT calculating the centripetal force!) At sides, just simply F = mv²/r since gravity acts perpendicular to centripetal force!) Therefore has no effect (cos90 = 0)

Is the velocity of a particle moving in a circle constant?

NO! Direction is always changing. Speed is constant.

What are the 2 equation for centripetal acceleration?

a = v²/r

a=w²r (w being angular speed = v/r)

How can you convert 15 revs per minute to angular speed?

w = (number of revolutions x 2 pi)/60 OR

f= number of revolutions/60 × 2pi

Why is an object in uniform circular motion considered to be accelerating, even if its speed does not change?

Acceleration is a vector quantity. The direction of the object is constantly changing, meaning the velocity is constantly changing. (Acceleration is Velocity/Time)

State the conditions for a mass to undergo simple harmonic motion? (2 marks)

Acceleration directed towards the equilibrium position and acceleration is proportional to negative displacement.

If asked to find the kinetic energy, what are the 2 equations you set equal to it to solve?

mgh

½ K e² (K being spring constant, e being extension)

How do you convert from angles to radians?

(angle x 2pi) /360

What are the 2 equations for the Centripetal force?

F = mv²/r = mw²r

What is the value for Gravitational constant?

6.67 × 10^-11

How do you convert from radians to angles?

(radian x 360) / 2pi

How can you calculate the Tension in a string with an object undergoing circular motion?

Centripetal force ± Weight of object.

Calculate the angular velocity of the Earth as it moves around the sun

using w = 2pi/T (T being the time Earth takes to complete 1 revolution around the Sun)

2pi / (365×24×60×60 = 32×10^6) = 2×10^-7 rads^-1

How can you convert rpm to rads^-1

(rpm x 2pi)/60

What are the units for angular speed

rads^-1

Is the speed of an object undergoing circular motion assumed constant?

Yes.

What is the definition of Simple Harmonic Motion? (2 marks)

• An oscillation in which the acceleration of an object is directly proportional to its displacement in the negative direction from its equilibrium position, and is directed towards the equilibrium.

What is the relationship between the acceleration and displacement of an object undergoing SHM?

a ∝ -x

What is the “restoring force”?

• The force that is always pushing or pulling the object back to the equilibrium position.

What does the size of the restoring force depend on?

• The displacement from the equilibrium position (the further away, the greater the force)

Why does the speed of an object in Circular Motion remain constant?

• The centripetal force acts perpendicular to the direction of motion. Therefore, using w = F x Dcosθ we see if θ = 90 degrees work done will be 0 (so constant speed)

What is meant by centripetal acceleration?

• If an object is moving in a circle, centripetal acceleration is the acceleration of the object directed towards the centre of the circle.

What is meant by centripetal force?

• Force towards the centre of the circle responsible for the centripetal acceleration.

What is centripetal force?

Any force which causes circular motion.

What is the equation for centripetal force?

(F=ma)

How does linear velocity relate to the angular velocity?

Linear velocity (v) = angular velocity (w) x radius r

Where does the change in velocity of an object in circular motion always point towards?

Centre of the circle, since change in velocity is acceleration and the centripetal acceleration acts in the same direction as the centripetal force, which we know acts towards the centre of the circle.

What is the definition of SHM?

a = -w²x where w is 2pif -m frequency of oscillation. - since displacement is negatively directly proportional to acceleration.

What is gradient of an acceleration-displacement graph?

-w² ~(angular frequency)

Where does the resultant (restoring) force act in SHM?

Towards the centre of oscillation (the equilibrium position)

Where does the restoring acceleration act in SHM?

Towards the centre of oscillation (the equilibrium position) This is because force acts in the same way as acceleration.

Does the restoring force act opposite to displacement in SHM?

Yes, since we know a ∝ -X, and we know that F and a act in the same direction.

What are the 2 conditions required for SHM to occur?

1) The acceleration is proportional to the displacement

2) The acceleration is in the opposite direction to the displacement.

How do an acceleration-time and a displacement-time graph differ in simple harmonic motion?

Reflected in the x-axis.

What is the equation for displacement in SHM?

x = Acos(wt)

A is the amplitude (radius),

w = 2pif

Why is equation for displacement in SHM only an approximation?

Since it uses the small angle approximation, making it only true when the angle of displacement is >10 degrees.

What is the equation to calculate phase difference between 2 oscillations in SHM?

2pi t/T (only works when oscillations have same frequency/wavelength meaning it is a coherent oscillator)

Why does a pendulum have maximum velocity when displacement is 0?

Since taking the gradient at a maximum results in 0. This is also because there is no restoring force on the object meaning there is no acceleration so no change in velocity, meaning it is at its maximum.

What are the 2 equations for velocity?

v=+-2πf(A²-x²)^1/2 or

v=+-w(A²-x²)^1/2 (w=2πf)

What is the equation for maximum velocity?

Velocity occurs when displacement is 0

Since v=+-w(A²-x²)^1/2, make x = 0 and cancel out the A² and the square root ()^1/2 to get:

Vmax = +-wA (A being the amplitude (radius)

Why do the velocity equations for SHM have +-?

Since velocity has direction, it takes into account the 2 different directions the pendulum could be travelling.

What are the equations for acceleration?

a = -w²x

a = -w²rcos(theta)

since acceleration is directly proportional to the negative displacement.

What is the equation to find the max acceleration?

a = -(w²)A - if finding the acceleration

a = (w²)A - if finding the magnitude of the acceleration.

What is w equal to?

Angular speed/frequency: (2pif)

What is the difference between the displacement and acceleration time graphs in SHM?

They are flipped.

What is the difference between the velocity time graph and the displacement/acceleration time graph in SHM?

Velocity = sin(x)

Displacement = cos(x)

Acceleration = -cos(x)

sin(90-x) = cos(x)

How to find maximum value of displacement, velocity and acceleration?

Displacement = A

Velocity = wA

Acceleration = w²A

What is the total potential energy and kinetic energy called in SHM?

Mechanical energy

When is Kinetic energy greatest in SHM?

At equilibrium point

When is Kinetic energy lowest in SHM?

At maximum amplitudes

When is Gravitational Potential Energy at maximum in SHM?

When at maximum amplitudes

When is Gravitational Potential Energy at minimum in SHM?

When at equilibrium position.

Does a kinetic energy-time graph ever become negative?

No

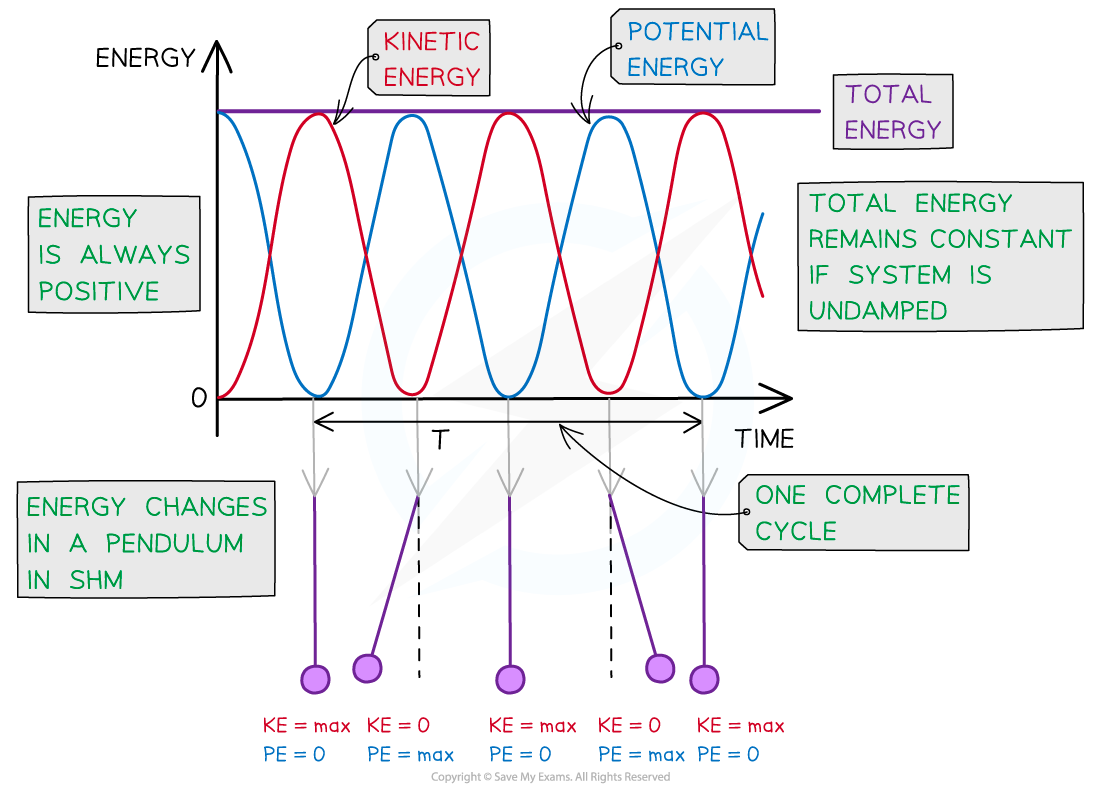
What is the definition of frequency in SHM?

The number of completed cycles (360 degrees) that occur per second.

What’s the phase difference between the displacement and the velocity of an object in SHM?

90 degrees

What is a closed system?

System where energy does not enter or does not leave.

Are all undamped oscillators considered to be a closed system?

Yes, no energy is lost or gained. (Energy of simple harmonic system remains constant)

Explain the kinetic energy and elastic energy states for a stretched spring at its maximum displacement?

Kinetic energy = minimum (amplitude is greatest - furthest away from its equilibrium position)

Elastic potential = maximum (string is at its most stretched point)

Explain the kinetic energy and elastic energy states for a stretched spring at its equilibrium position?

Kinetic energy = maximum (amplitude is 0 - at its equilibrium position)

Elastic potential = minimum (string is at its least stretched point)

What is the equation for angular speed for mass-spring system?

w = (k/m)^1/2

k is spring constant

m is mass

What is the equation to find the period of oscillations for a mass-spring system?

T = 2π(m/k)^1/2

T is the time taken for 1 complete oscillation

Allows you to work out the spring constant!

What are the 2 equations to work out the spring constant?

F= -(k)e (- for displacement)

T = 2π(m/k)^1/2 rearranged

What is the graph you plot for time and mass when investigating the mass-spring system?

T² on y-axis

Mass on x-axis

Why do you plot a time²-mass graph for investigating mass-spring system?

Since T = (m)^1/2

What are the 3 variables you vary in the mass-spring system experiment?

Amplitude, Spring Constant and Mass.

How are T an k related?

T (time taken for 1 oscillation to occur)

T = (1/k)^1/2

How does adding spring constants with springs in series and parallel work?

Series: k1 +k2 +k3…

Parallel: 1/ktotal = 1/k1 +1/k2….

(Just like finding resistance in electricity)

Is the restoring force always opposite to motion in s simple pendulum?

Yes, since as the pendulum moves towards maximum amplitude for example, the restoring force will be acting towards the equilibrium position.

What is the equation to work out the time period of a simple pendulum?

T = 2π (l/g)^1/2

where l is the length of the string

What are the 3 assumptions for the simple pendulum equation?

1) The amplitude of oscillations is less that 20 degrees (since using small angle approximation and works for less than 10 degrees on either side)

2) Length of pendulum is from the fixed position to the centre of mass of the bob

3) No damping acting on the oscillator

What are the 3 variables you can change in the simple pendulum experiment?

Length, Mass, Amplitude

What does it mean to be a free vibration system?

System displaced and left to oscillate

How is resonant frequency caused?

Striking metal or stretching and releasing a mass on a spring.

What is another word for resonant frequency?

Natural frequency

What does it mean to be a forced vibration system?

Objects that have oscillations produced when a driving force is placed on it.

Is the driving force in a forced vibration system constant?

Yes, it is constantly acting on the object.

What frequency does a free oscillator system oscillate at?

Natural frequency

What frequency does a forced oscillator system oscillate at?

Driving frequency

What are damping forces?

Resultant forces which cause work to be done from an oscillating system to the surroundings (frictional forces).

What are dampers?

Parts of systems which are designed to produce damping forces.

What are the 4 types of damping?

Light, Heavy, Critical, Over.

What are the effects of light and heavy damping and their graphs?

Light damping requires alot of time for the oscillator to stop oscillating.

Heavy damping requires less time for the oscillator to stop oscillating.

[Heavier the damping, the faster the amplitude of the oscillations decrease]

[Both keep the time period and frequency almost constant]

What are the effects of critical and over damping and their graphs?

Critical damping reduces the amplitude in the shortest possible time without 1 oscillation and returns to its equilibrium position (car suspension systems)

Overdamping reduces the amplitude without making 1 oscillation over a longer time period. (heavy doors)

[Both return to equilibrium position without making another oscillation]

4 types of damping?

What is resonance?

When the driving force approaches the natural frequency of a lightly damped system, the system gains more and more energy, causing it to vibrate more with a rapidly increasing amplitude.