DAY 12 FORMULA-CONICS

GENERAL EQUATIONS OF CONIC SECTIONS

HOW TO IDENTIFY IF THE EQUATION OF CONIC SECTIONS IS A PARABOLA

METHOD 1: DISCRIMINANT

METHOD 2: GENERAL EQUATION

HOW TO IDENTIFY IF THE EQUATION OF CONIC SECTIONS IS A CIRCLE

METHOD 1: DISCRIMINANT

METHOD 2: GENERAL EQUATION

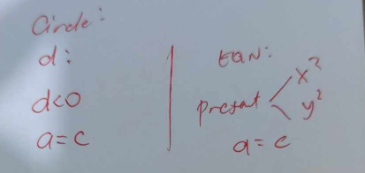
HOW TO IDENTIFY IF THE EQUATION OF CONIC SECTIONS IS A ELLIPSE

METHOD 1: DISCRIMINANT

METHOD 2: GENERAL EQUATION

HOW TO IDENTIFY IF THE EQUATION OF CONIC SECTIONS IS A HYPERBOLA

METHOD 1: DISCRIMINANT

METHOD 2: GENERAL EQUATION

PARABOLA:

1

AT ORIGIN, FORMULA OF PARABOLA OPENING LEFT AND RIGHT

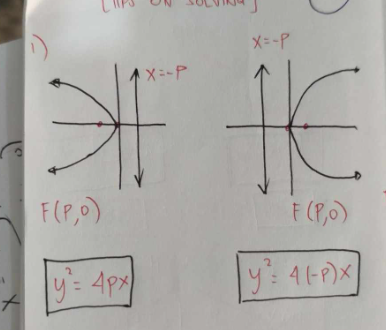
NOT ORIGIN, FORMULA OF PARABOLA OPENING LEFT AND RIGHT

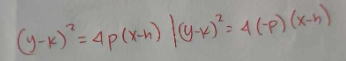
AT ORIGIN, FORMULA OF PARABOLA OPENING DOWNWARD AND UPWARD

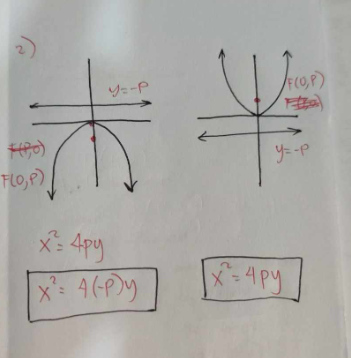
NOT ORIGIN, FORMULA OF PARABOLA OPENING DOWNWARD AND UPWARD

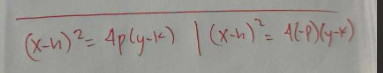
FORMULA OF LATUS RECTUM OF A PARABOLA

4P (ABSOLUTE VALUE)

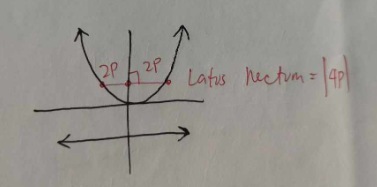
FOCAL LENGTH OF PARABOLA

P

LATUS RECTUM AND SEMI-LATUS RECTUM OF PARABOLA

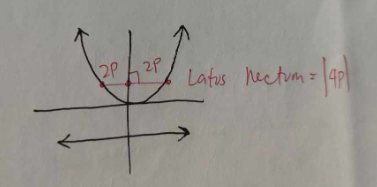
AXIS OF SYMMETRY OF PARABOLA

X=# OR Y=#

DIRECTRIX OF PARABOLA

X= -P OR Y= -P

CIRCLES:

1

FORMULA OF CIRCLE AT ORIGIN (0,0)

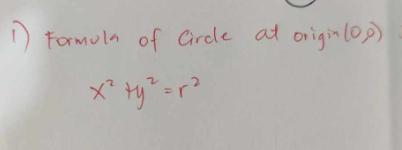
FORMULA OF CIRCLE AT NOT ORIGIN

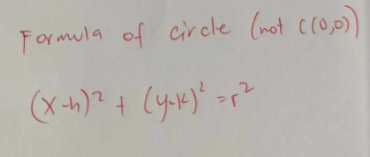
CIRCLE CENTER-RADIUS FORM AKA STD. EQN.

ELLIPSE:

1

ELLIPSE FORMULA AT CENTER (0,0)

ELLIPSE FORMULA AT NOT CENTER

ARBITRARY CONSTANT IN ELLIPSE FORMULA

MAJOR AXIS FORMULA

2a

MINOR AXIS FORMULA

2b

ELLIPSE B-SQUARED FORMULA OR RELATIONSHIP OF A,B,C (RELATIONSHIP OF SEMI-MAJOR, SEMI-MINOR, AND FOCI)

B² = A² - C²

LATUS RECTUM OF AN ELLIPSE (SAME WITH HYPERBOLA)

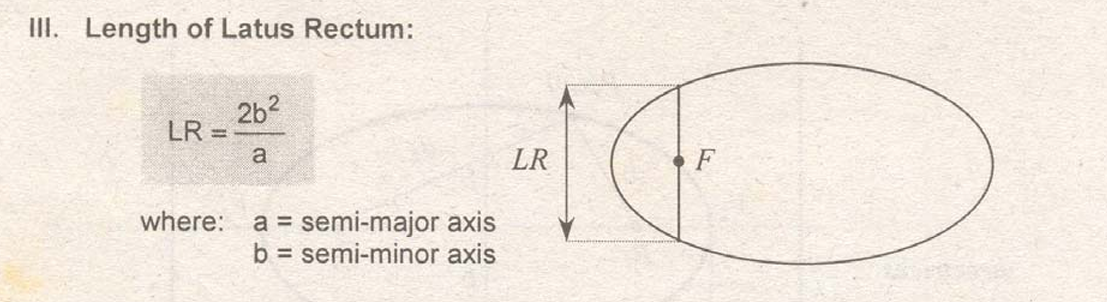
SEMI-MAJOR AXIS FORMULA

= A

SEMI-MINOR AXIS FORMULA

= B

AREA OF ELLIPSE

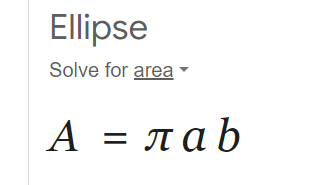
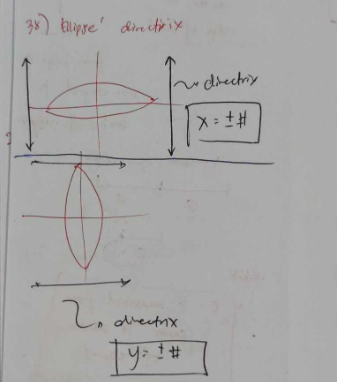
DIRECTRIX OF AN ELLIPSE

HYPERBOLA:

1

STANDARD FORM OF HYPERBOLA

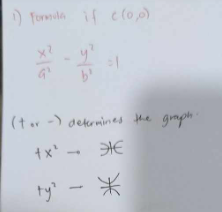
FORMULA OF HYPERBOLA AT ORIGIN (0,0)

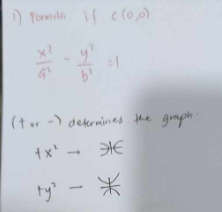
FORMULA OF HYPERBOLA AT NOT ORIGIN

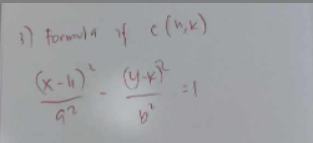
HYPERBOLA. B-SQUARED FORMULA OR RELATIONSHIP OF A, B, C

(RELATIONSHIP OF SEM-TRANSVERSE, SEMI-CONJUGATE, FOCI)

B² = C² - A²

CONSTANT FORMULA OF HYPERBOLA

2a=

TRANSVERSE AXIS FORMULA

SEMI-TRANSVERSE AXIS FORMULA

=A

CONJUGATE AXIS FORMULA

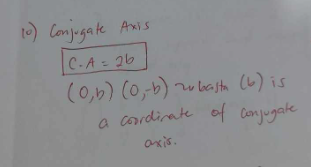
SEMI-CONJUGATE AXIS FORMULA

=B

ASYMPTOTE FORMULA AT ORIGIN

ASYMPTOTE FORMULA AT NOT ORIGIN

EQUATE THE STD FORM OF HYPERBOLA TO ZERO

DE-FACTOR THE EQN USING DIFFERENCE OF TWO SQUARES

SOLVE FOR Y

ECCENTRICITY OF HYPERBOLA FORMULA (2)

ECCENTRICITY OF HYPERBOLA FORMULA (additional)

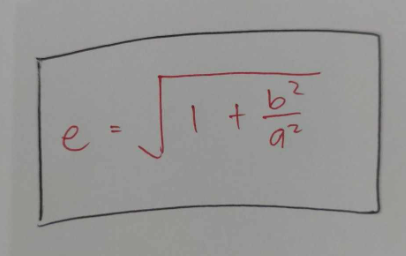
LATUS RECTUM OF HYPERBOLA