Exam 1 Rules and Definitions Shormann Precalculus

What people group are the oldest know mathematical documents from?

Babylonians (2500 BC to AD 260); not much is known of the pre-flood world.

solute divided by solution x 100

How do you find the % of solute in a solution?

commutative property for addition

if a+b=c, then b+a=c

Difference of 2 squares rule:

a squared - b squared = (a+b)(a-b)

polynomial in more than one unknown

one term, or a sum of individual terms of the form ax^n y^m z^p..., where a is a real #, x,y,z, etc. are unknown quantities, and n,m,p, etc. are whole #'s.

"What 2 factors, when multiplied together equal 'c', and when added together equal 'b'?"

What question can you think about when factoring a quadratic polynomial?

Equation of a line in General form

Ax + By + C = 0

fundamental theorem of algebra

any polynomial of degree 'n' has 'n' complex roots; NOTE: real #'s are also complex #'s if the form a+bi. In other words, the imaginary part =0

line

a width-less length; its location is represented on paper by using a pencil and straight edge.

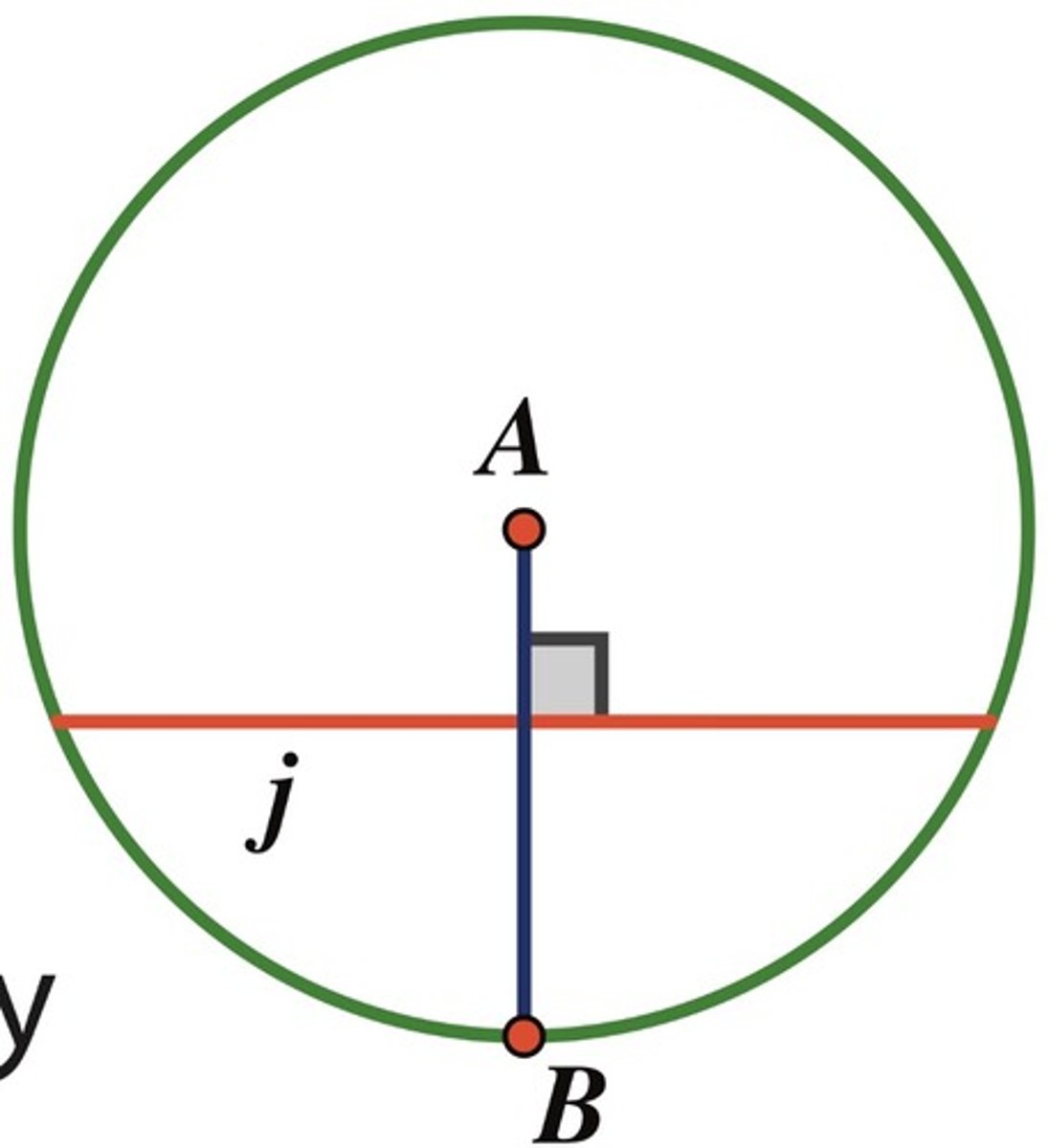
perpendicular bisector of a chord theorem

if any segment 'AB' passing through the center, 'A', is drawn perpendicular to any chord 'j', then it bisects the chord. The converse is also true: if any segment 'AB' passing through the center bisects any chord 'j', then it is perpendicular to the chord.

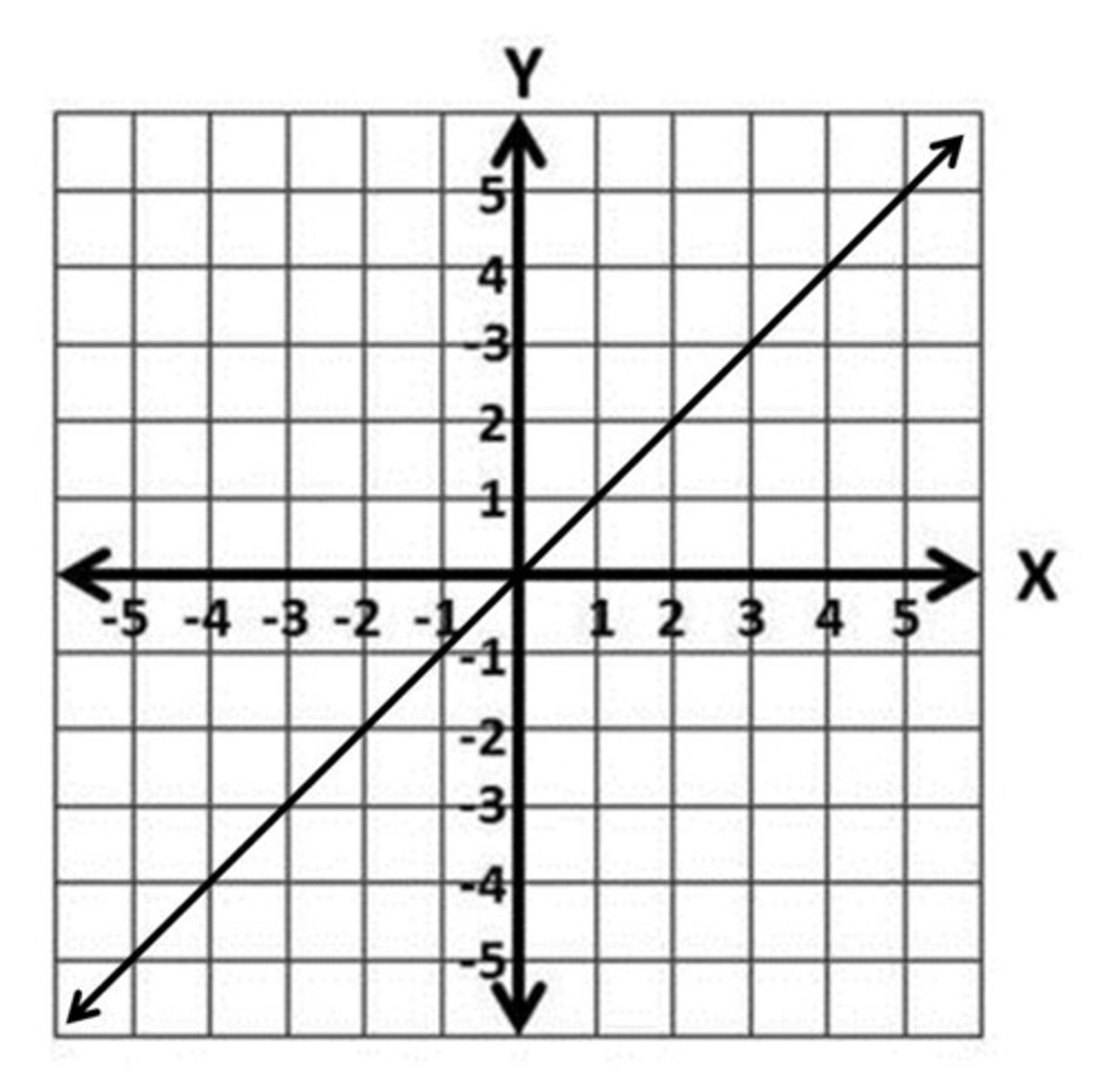
linear function graph

Name the type of function shown
f(x) = x:

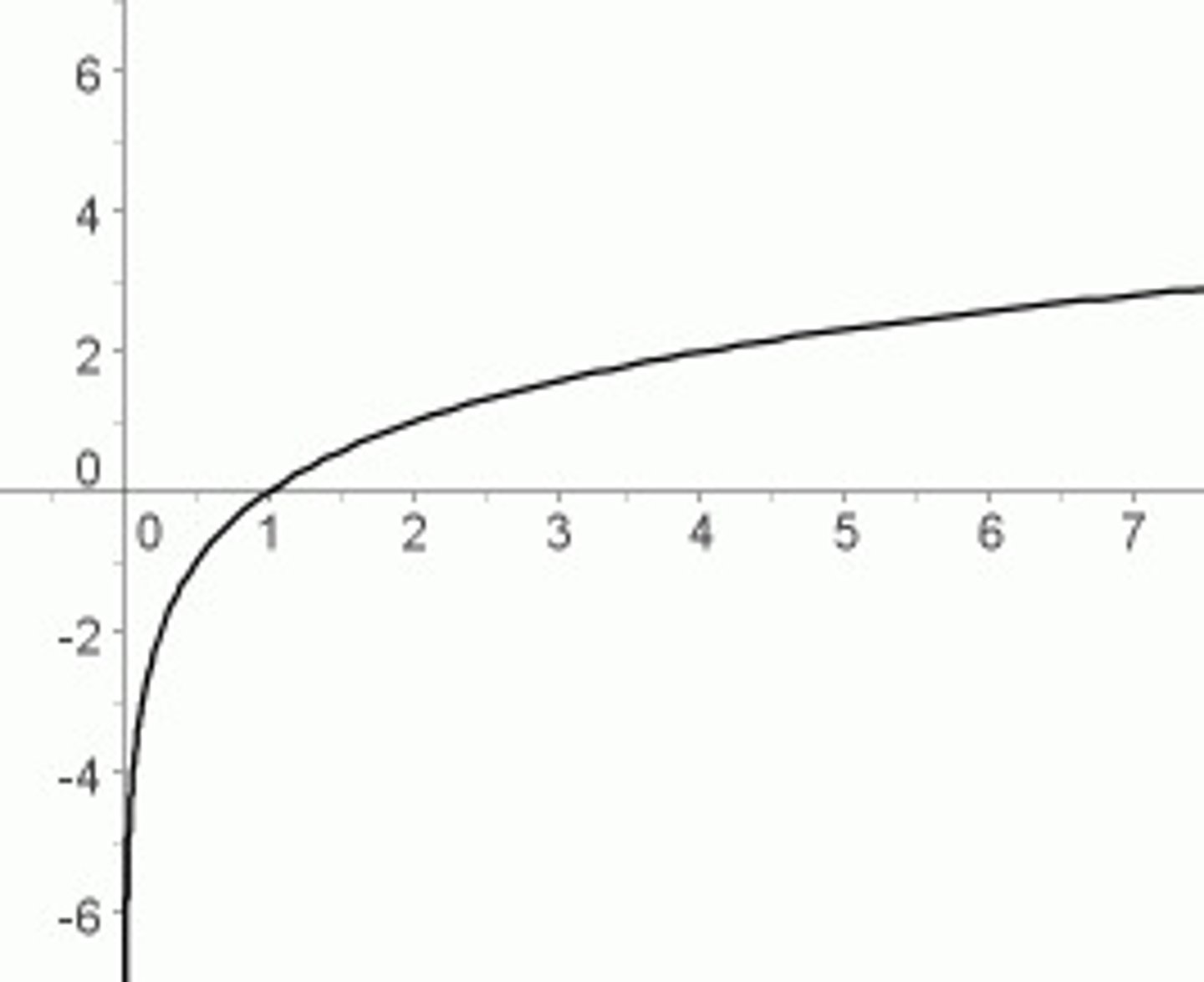
logarithmic function graph

name the type of function shown f(x)=log (sub b)times x for b>1

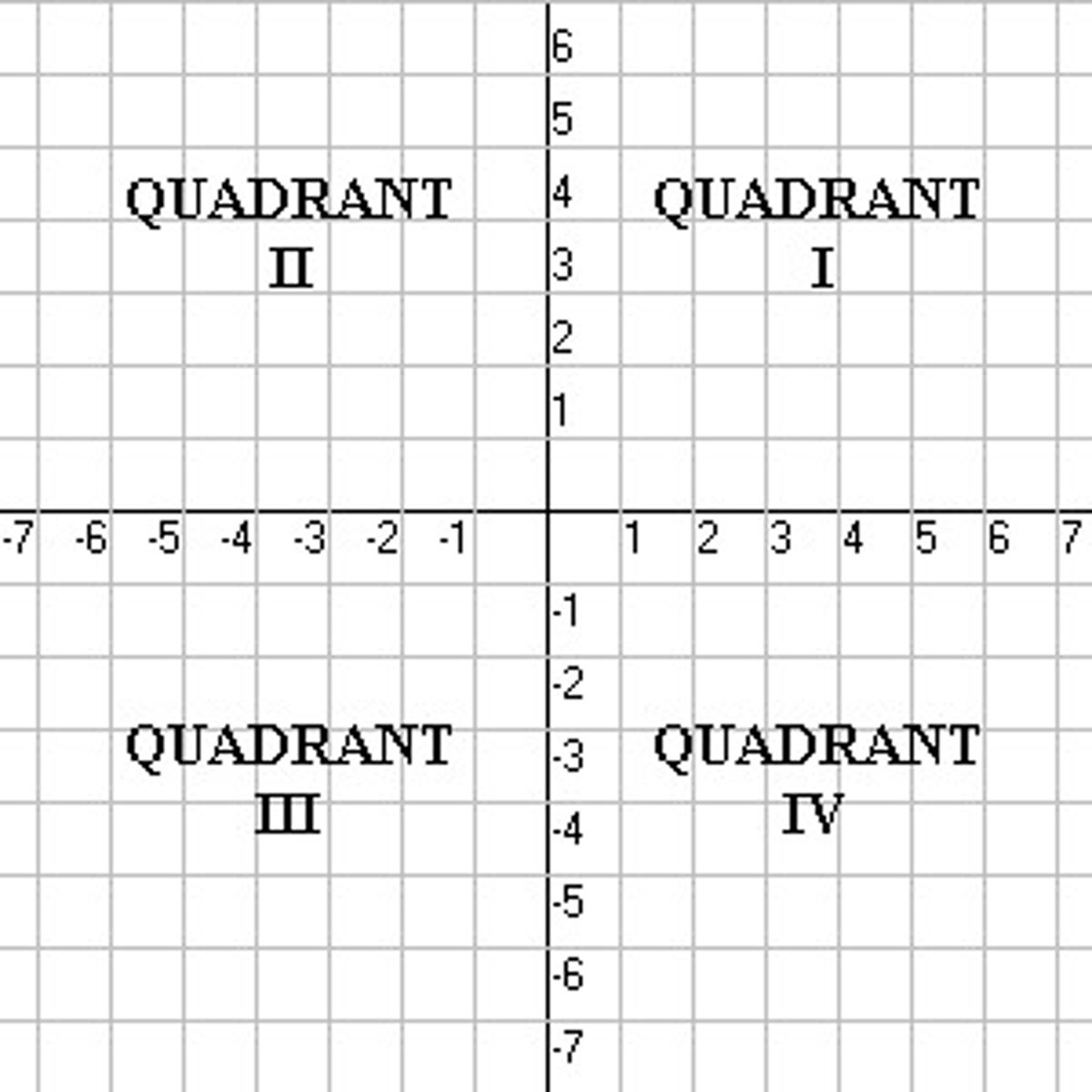
quadrant

the 4 parts of a coordinate plane, as described below:

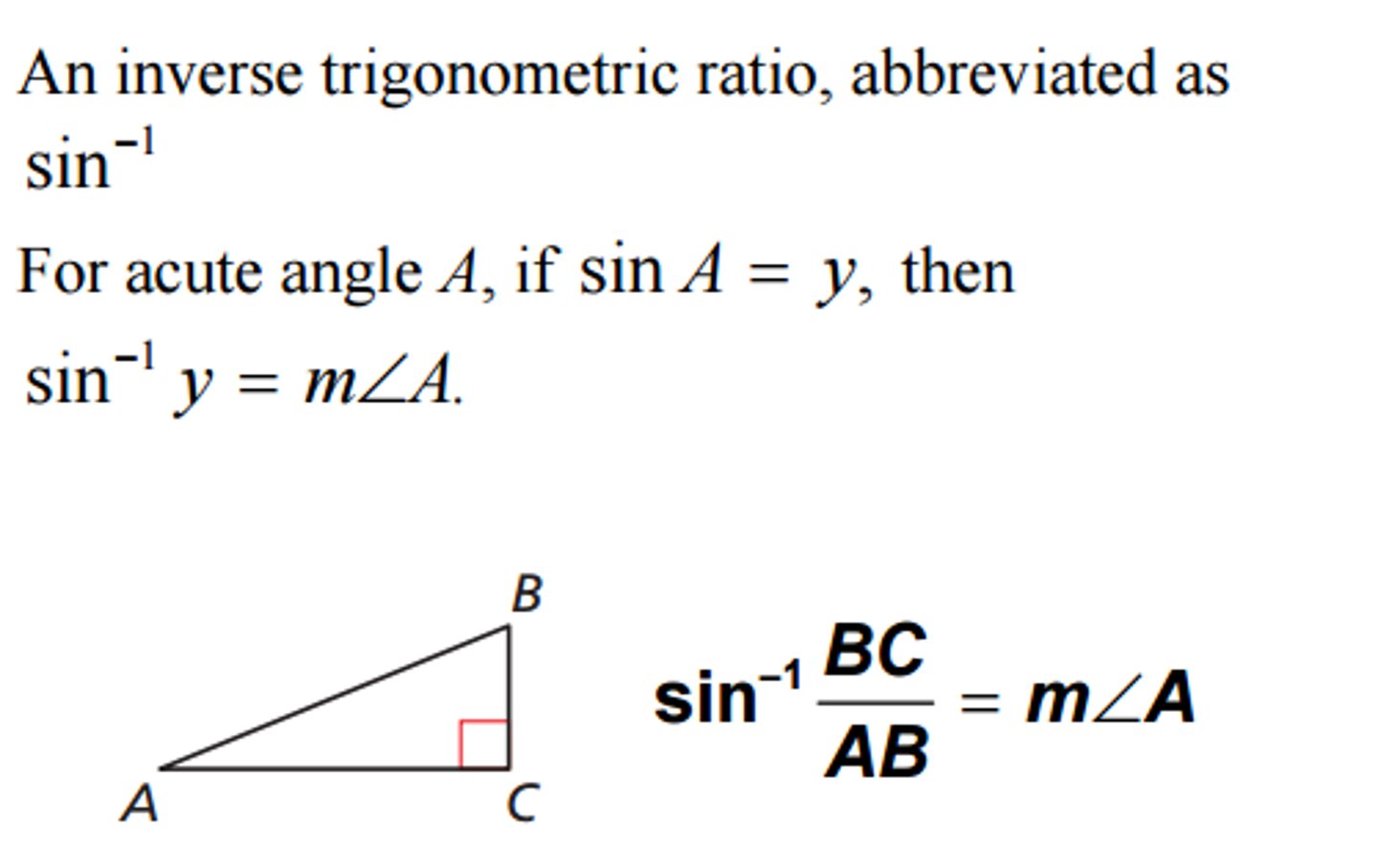
inverse sine function

opposite/hypotenuse

Parallelogram Law

the sum, or resultant, of any two vectors equals the diagonal of a parallelogram whose sides equal the magnitudes and directions of the 2 vectors.

Steps to convert from Rectangular to Polar Coordinates:

1. Get your bearings (draw the vector on a coordinate plane)
2. Draw a right triangle, marking the magnitude, M and direction, 'theta'.
3. Find M using the distance formula.
4. Find 'theta' using the inverse of tangent, recording its actual value relative to the positive x-axis.
5. Write answer in the form M angle (theta).

disjoint sets

two sets that have no elements in common

union

when referring to 2 sets, {A} & {B}, where all #'s belong to both sets. When both sets have an identical #, it is only included once when describing this.

intersection

when referring to 2 sets, {A} & {B}, where only the #'s that the sets have in common is referred to.

mass divided by volume

How do you calculate density?

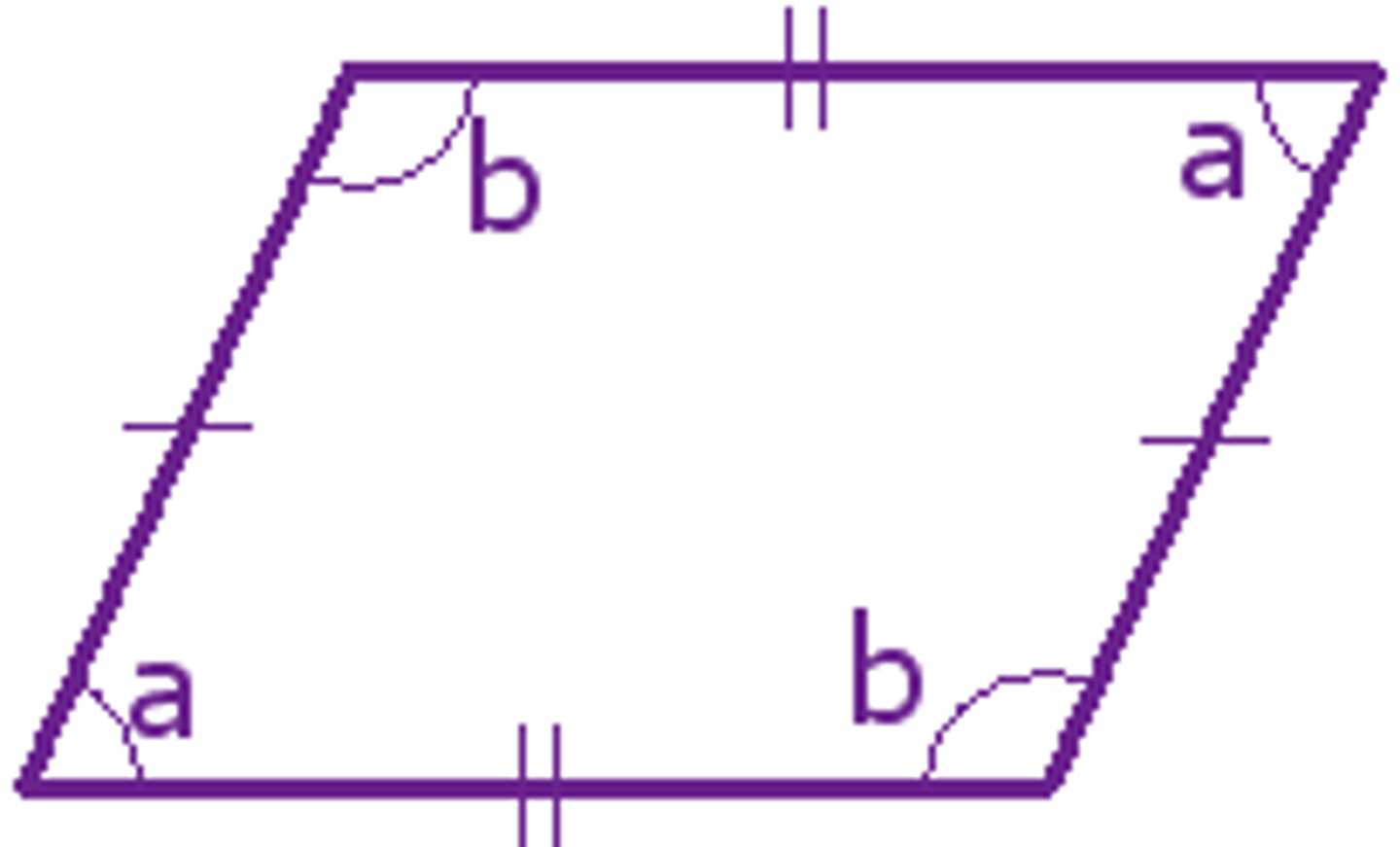
sas

2 triangles are similar if the lengths of 2 corresponding sides are proportional, and the angles between those sides are congruent: side, angle, side

vertex

where 2 polygon sides, or 2 angle rays, meet

cone

a solid with a circular base and a lateral surface that comes to a point

sphere

a solid, which is the set of points a given distance from a given point called the center

deductive reasoning

the process of applying rules. Mathematics is deductive. There are mathematical rules yet to be discovered.

hypothesis

the premise or initial facts started with the "if" statement. In science courses, it is often referred to as an educated guess.

A3

From Euclid's 5 axioms, or common notions:
If equals be subtracted from equals, the remainders are equal.
If a=b and c=d, then a-c=b-d

horizontal line test

a graph on a coordinate plane is a one-to-one function if a horizontal line intersects the graph at only one point.

slope

a ratio expressing the change in the dependent variable (y) with respect to the independent variable (x). Also referred to as "rise over run", "change in y over change in x", and "delta 'y'/delta 'x' where "delta (triangle shape)" = "change in".

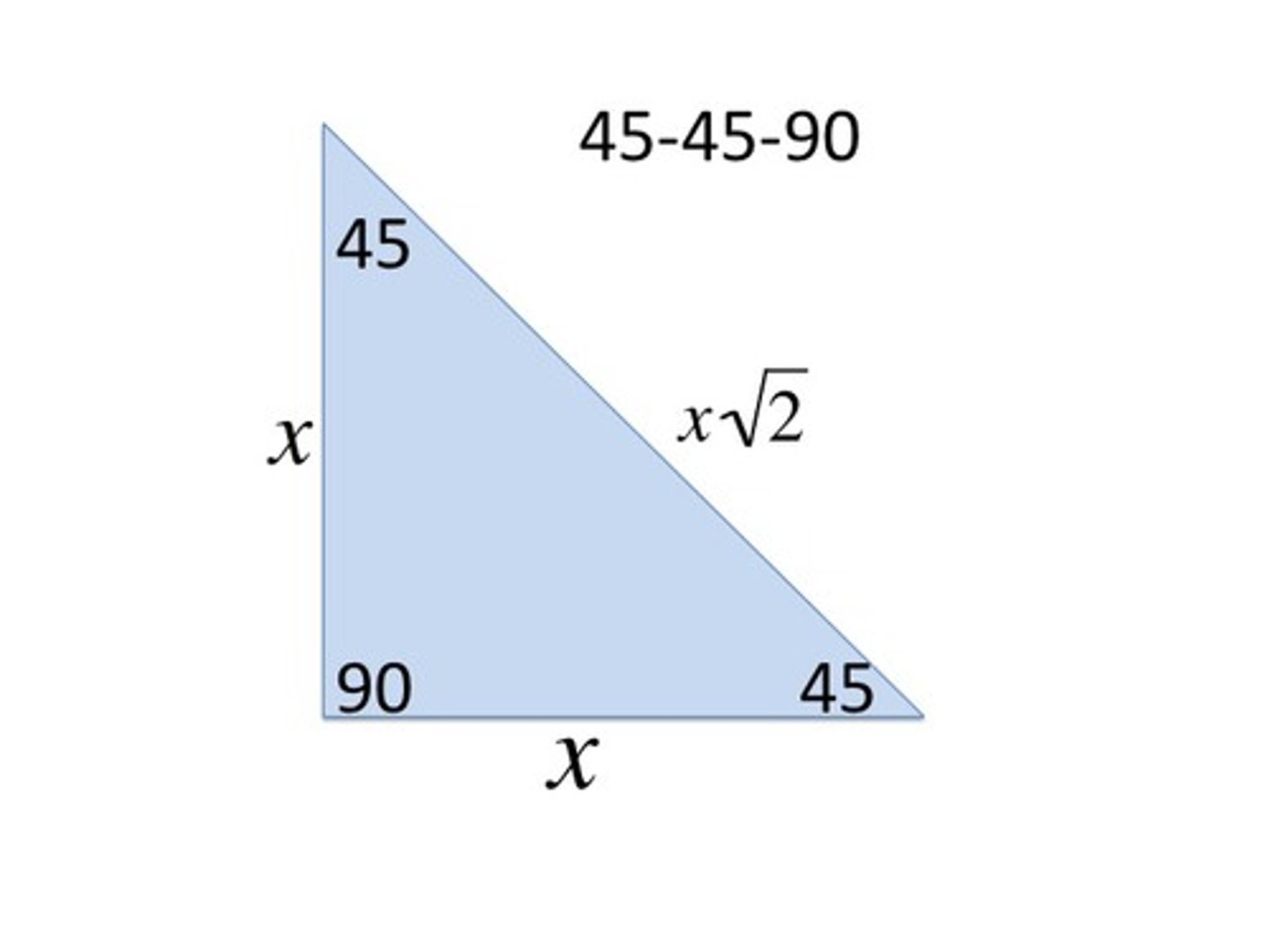
ratios of 45-45-90 right triangle

polar form

a way to represent a vector by its magnitude (M) and direction (degrees-"theta"). Often written using the notation M (angle) "theta"

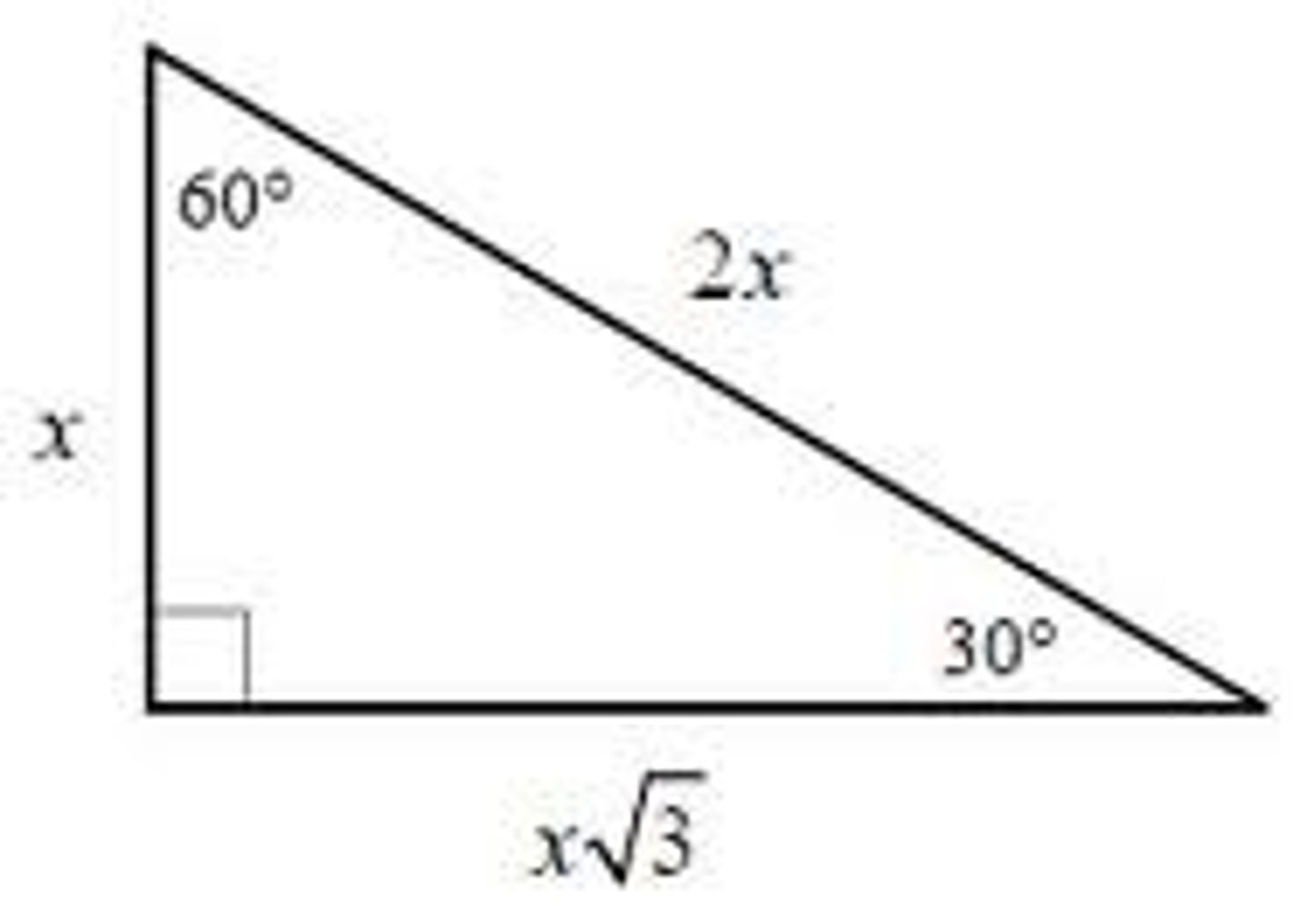
30-60-90 triangle

infinitesimally

a quantity whose value is decreasing without bound. The idea that a value can be close to, but not equal to, zero. super small change; instantaneous.

inductive reasoning

the process of discovering rules.

deductive reasoning

the process of applying rules

numeral

a symbol or symbols used to express the idea of #

abstract

dealing with the properties & ideas of things

concrete

a word used to describe real objects; abstract ideas are always based on real things.

digit

any of the Hindu-Arabic numerals 1-9, and 0

natural #'s

counting #'s; 1,2,3...etc.

whole #'s

counting #'s & zero

integers

whole #'s & all negative #'s

real #'s

any number used to describe a positive or negative #; includes all integers & all decimal & fractions.

rational #

a # that can be written as a fraction of integers

irrational #

a # that cannot be written as a fraction of integers; have non-repeating decimal patterns

trichotomy axiom

for any 2 real #'s and b, exactly one of the following is true:
a<b a=b a>b

square root

if x is greater than 0, then the square root of x is the unique positive real # such that the square of the square root of x = x.

imaginary #'s

the result of taking the square root of a negative number. Normally the square root of -1 is factored out and exchanged for the symbol "i". i squared = -1

complex #'s

numbers that have a real part & an imaginary part: ex. a+bi
note - all real #'s are complex with b=0

subset

a special group of elements that is entirely contained within a larger set.

logic

the art of reasoning well.

idea

a number is an _______.

mathematics

This is Dr. Shormann's definition of what term:
"_______ is the language of science and a God-given tool for measuring and classifying pattern and shape."

{}

this represents a 'set' of things

U

union of 2 sets

upside-down U

intersection of 2 sets

empty set; null set

An "o" with a diagonal line through it

vertical line '|'

means "such that"

A fancy, bold 'N' represents what in set notation?

"the set of natural #'s"

A fancy, bold 'Z' represents what in set notation?

"the set of integers"

A fancy, bold 'Q' represents what in set notation?

"the set of rational #'s"

A fancy, bold 'R' represents what in set notation?

"the set of real numbers"

universal set

The enclosing rectangle of 2 sets depicting a Venn diagram; maybe illustrating an intersection or union.

Jeremiah 33:3

"Call unto me, and I will answer thee, and shew you great and mighty things which thou knowest not." (KJV)

sexagesimal

the base 60 numeral system which we still use today (60 seconds in a minute, 60 min. in an hour, 360 degrees in a circle.) This originally comes from the ancient Babylonians.

one

Any # divided by itself equals what?

1/x

What is the reciprocal of x?

Logarithm rule

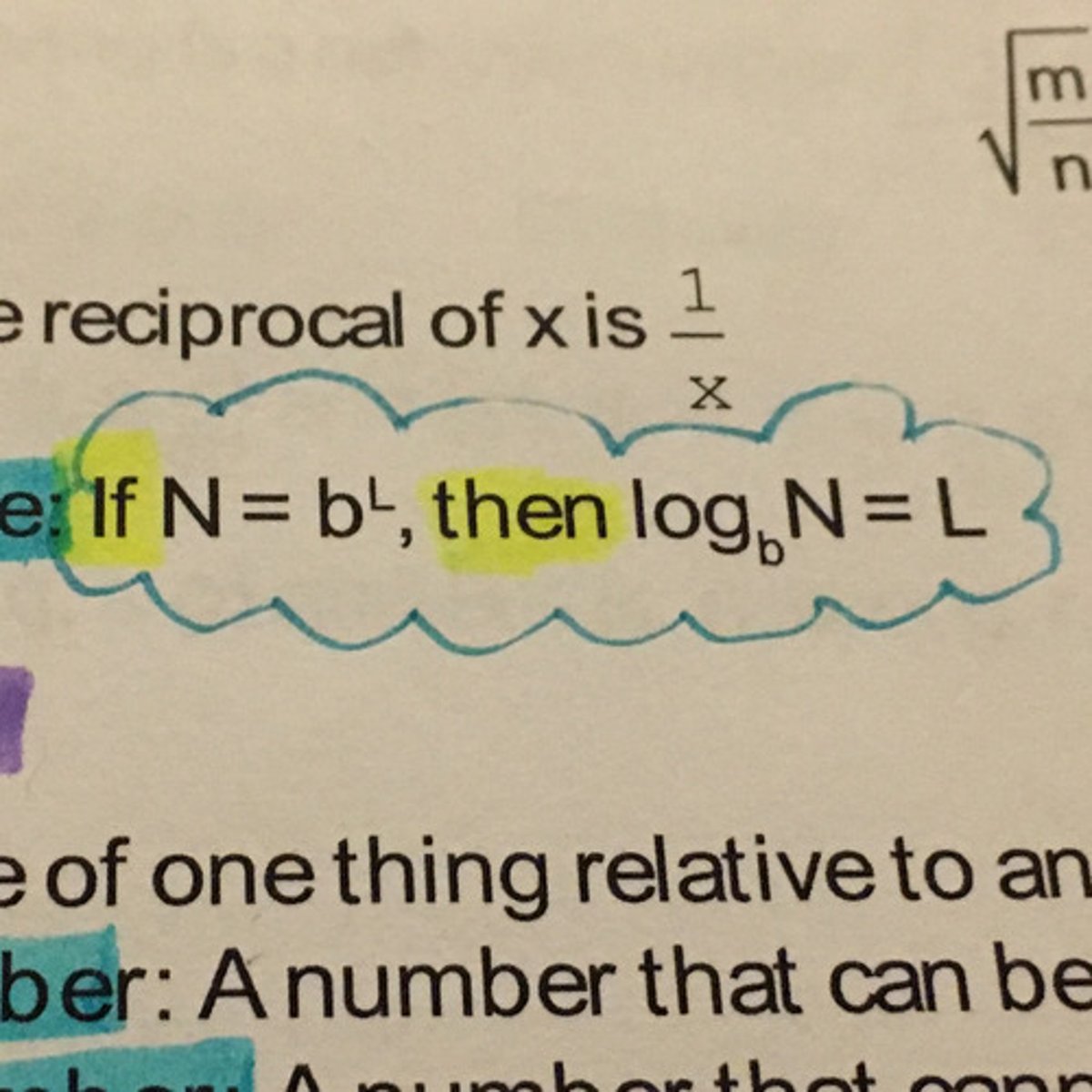
ratio

the size of one thing relative to another.

fraction

part of a whole; a numerical quantity that indicates division of one # by another.

prime #

a # that is only divisible by itself & 1, such as 2,3,5,7 etc.

numerator & denominator

What is the "top" and "bottom" # of a fraction respectively?

logarithm

in any exponential relationship of the form N=b to the 'L' exponent; 'L' can be referred to as the _______ of N

proportional

having a constant ratio

analogy

resemblance in some particulars between things otherwise unlike; similar

Logos

the original Greek manuscripts used this in place of 'Word'

proportion

equal ratios

circumference divided by the diameter of a circle

Where does the calculation for "pie" come from?

Natural log is also called Log 'e'. What is it's value and where is this # used?

the 'e' is named for the scientist, Euler. Euler's # is approximately = to 2.718 and is used in science, specifically in biology to measure bacteria.

Log 10 & Log 'e'

What are the 2 most commonly used logarithms?

distance divided by time

How do you calculate rate?

1000 grams

What does 1000mL of water weigh?

commutative property of multiplication

if ab=c, then ba=c

associative property for addition

(a+b)+c = a+(b+c)

associative property for multiplication

(a times b)c = a(b times c)

distributive property

a(b+c) = ab + ac

additive identity

a+0=a ; any # plus zero equals that #

multiplicative identity

a(1) = a ; any # times 1 equals that #

power rule for exponents

if m and n are real #'s and x does not = zero, then

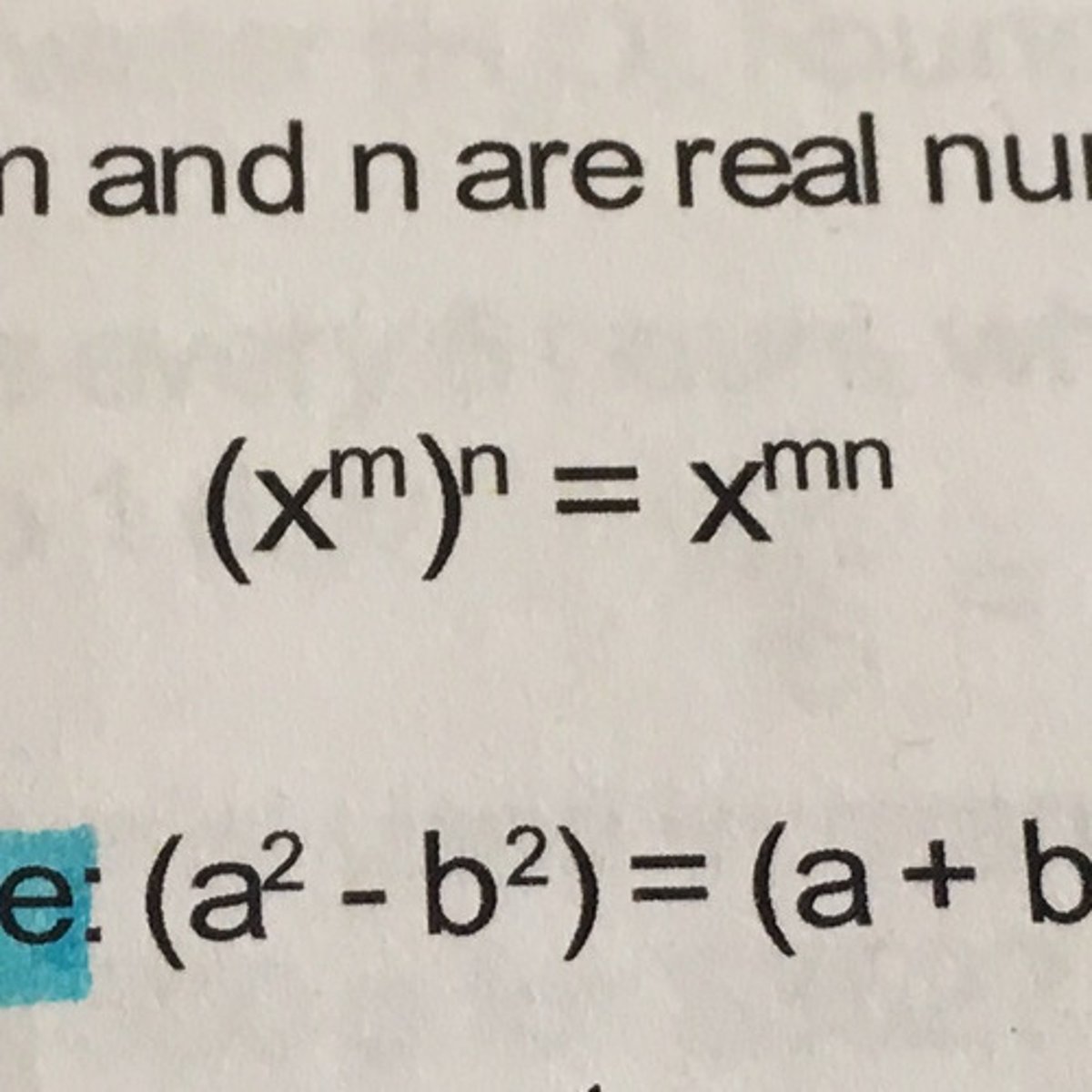
Logarithm Laws:

algebra

a generalization of arithmetic, where letters representing #'s are combined according to the rules of arithmetic, often to solve for a unknown value

one

in algebra, you don't have to write the 1 (one)

polynomial in one unknown:

one term, or a sum of individual terms of the form ax^n, where a is a real #, x is an unknown quantity, and n is a whole #.

Hisab al-jabr

a book written by Islamic astronomer meaning "science of transposition & cancellation." This is where we get 'algebra' from. (sound it out)

additive property of equality

if a, b, and c represent real #'s, and if a=b, then a+c=b+c also: c+a=c+b

multiplicative property of equality

if a, b, and c represent real #'s, and if a=b, then ca=cb also: ac=bc
and: a/c = b/c

parallel lines

"train tracks" have the same slope

perpendicular lines

where 2 lines cross making 4 right angles; these lines have slopes that are negative reciprocals of each other

slope

a ratio expressing the change in the dependent variable (y) with respect to the independent variable (x). Also referred to as "rise over run", "change in y over change in x"; also:

delta

"change in"