CALCULUS 2 (older)

Area under a curve using right point rectangles

Rn

Area under a curve using left points

Ln

Δx equation

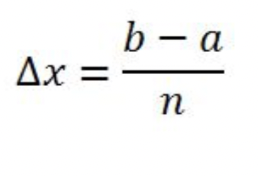
• “width” of each rectangle

• a is starting point for function’s area, b is ending point.

x_i equation

• to find the x-position to plug into for height f(xi)

• i = 1 to n

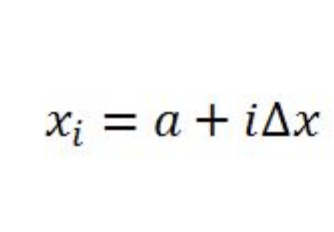
n

number of rectangles to estimate area

Definite Integral Equation / Riemann Sum

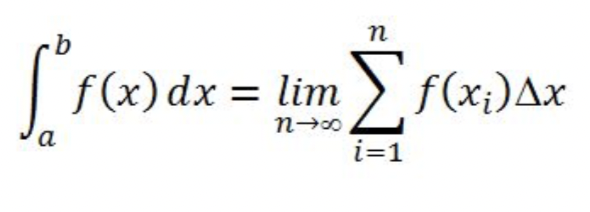
• dx is the same as Δx

Question Type : “Find an expression for area under the graph of f as a limit. Do not evaluate the limit.”

Use definite integral / Riemann sum formula

Sigma Notation (5 rules to know)

Properties of The Integral (to use when evaluating)

• you use to “evaluate the integral”

Integrals are a ____ area

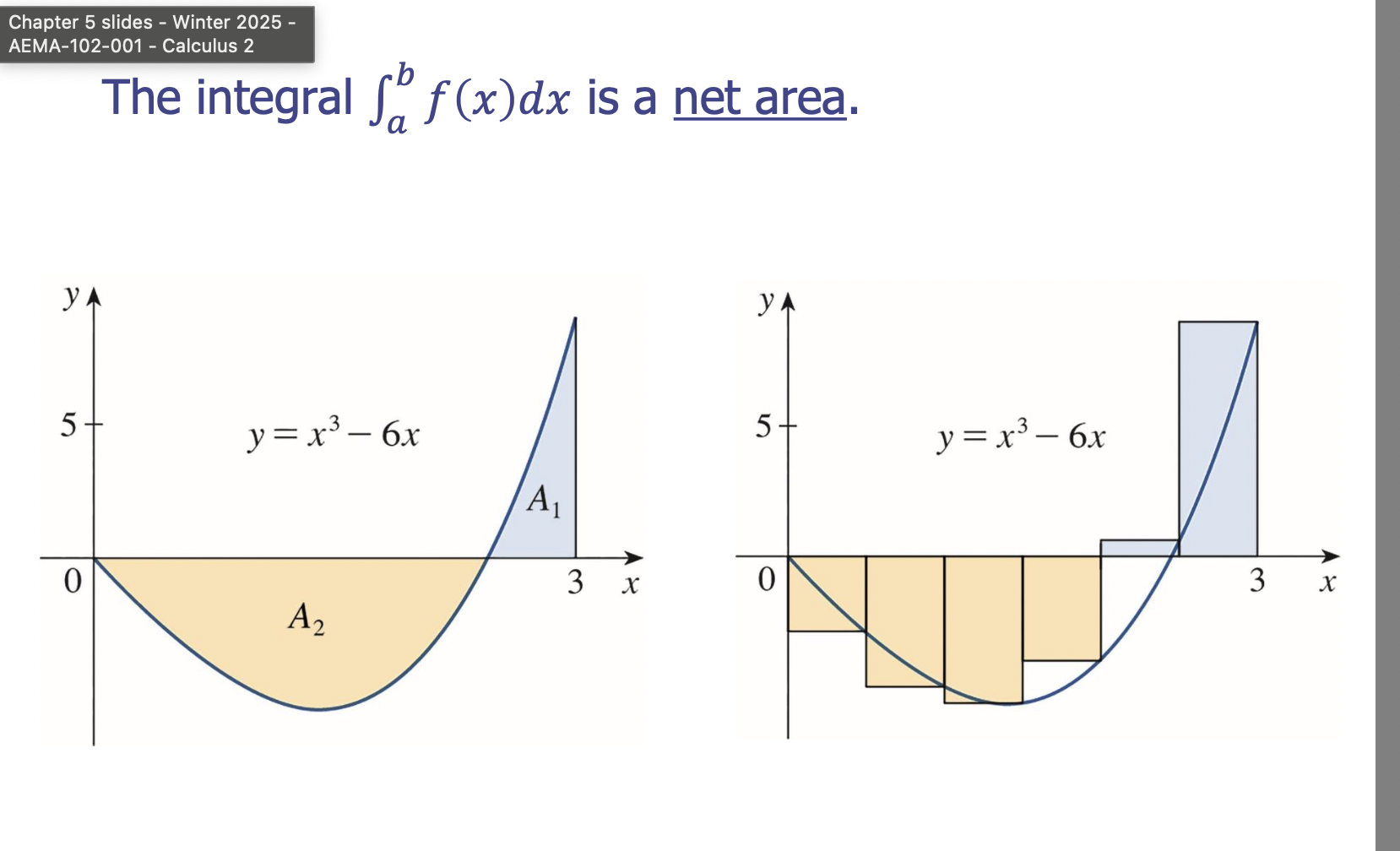
Question Type: express the limit as a definite integral on the “given integral”

• use the definite integral equation and then just plug in “x” in for “x_i”

• dx replaced with change in x

Question Type: What do you use to “evaluate” the limit as n approaches infinity?

you use the “sigma notation” 5 identities (or same thing)

Fundamental Theory of Calculus Part 1

• The g(x) integral is inside the f(x) integral (x in between the a,b interval)

• just explains doesn’t help evaluate

Fundamental Theory of Calculus Part 2

• how to evaluate integral (a,b)

• this means its a definite integral (net area)

If F’(x) = f(x), a definite integral is a _________.

number (net area).

If F’(x) = f(x), an indefinite integral is a ________.

function (antiderivative).

• add + C

TABLE OF INDEFINITE INTEGRALS

An indefinite integral happens when… (in words)

the integral of a function ends up being equal to its anti derivative … F’(x) = f(x)

What are substitutions in reverse?

the chain rule

What 2 shortcuts should you use for evaluating Definite and Indefinite integrals…

1. the chain rule

2. substitution

derivative of the antiderivative equals…

the function

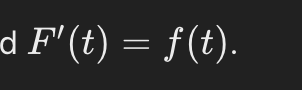
CHAIN RULE (use when you see a function inside a function)

to simplify after the FTOC steps…

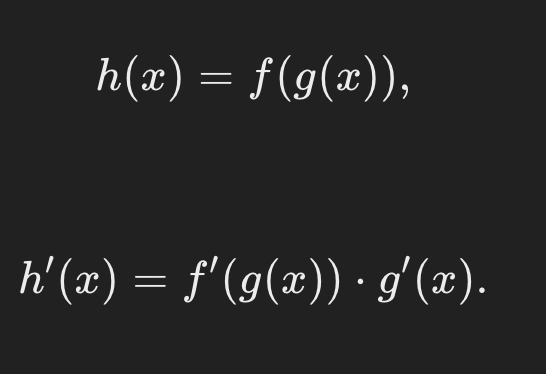
ln graph

ln(e) = 1 !

Derivative of exponential term

derivative of exponential function “e”

always equal to itself

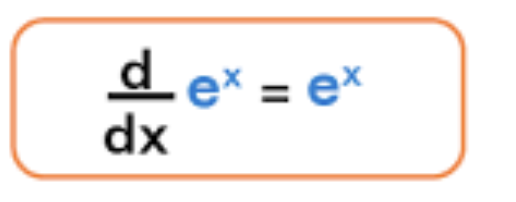
derivative of a term like ln(e^2x)

since ln(e) cancels out to 1 it will = 2x

ln(e)

=1

derivative of lnx

= 1/x

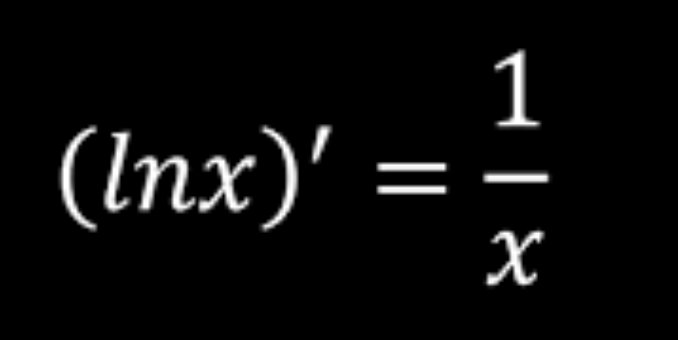
Trick for square roots

To find the volume using slices and shells formulas you know to derive with respect to x or y (dx versus dy)

Given where you can visualize direction the thickness were to be if you were to try to squeeze the shape

SLICES formula for predicting volume

V = Sba pi (outer radius)² x (inner radius)²

-draw a washer (or just a circle — depends) through the shape

SHELLS formula for predicting volume

V = Sba 2pi x f(x)dx

-can also differentiate with respect to

What’s the only thing you have to do when

Steps to antiderivative solving when finding the volume of a shape (slices or shells)

1. Set up formula right (slices or shells choose)

2. If in terms of x or y, reorganize the main function formula

3. For shells:

   1.) nothing special about the shape, just plug in the f(x) like formula suggests

   2.) bring outside 2pi , and find antiderivative of that function

   3.) do the integral line b-a thing

   4.) evaluate transformed function with b and a plugged in F(b) - F(a) and get answer

   For slices:

   1.) put rearranged function in for inner radius and outer radius in the ² brackets

   2.) find antiderivative of those functions

   3.) then do the integral stuff for those antiderivatives setting up a b - a (b and a plugged into the transformed functions) for both outer and inner radius.

   4.) what you get for outer - inner is answer

Steps for problems requiring substitution:

1. find what u should be, write it down (it’s related to the other term)

2. write down what du/dx is (derivative of u)

3. write down what x is in terms of u.

4. find what u is equal to when x=a and x=b

5. Now solve the whole thing using antiderivative rules

   -take antiderivative of terms for example

   -use “I” thing with b and a

How to find area bounded by 2 lines…

S (top - bottom) dx

• everything in terms of y = … x

S (right - left) dy (looked at from side or y-axis)

• everything in terms of x = …y

• simplify what you can then use integral rules

To know “Chapter 7” trig identities

rule for a sin^ and cos^ finding integral

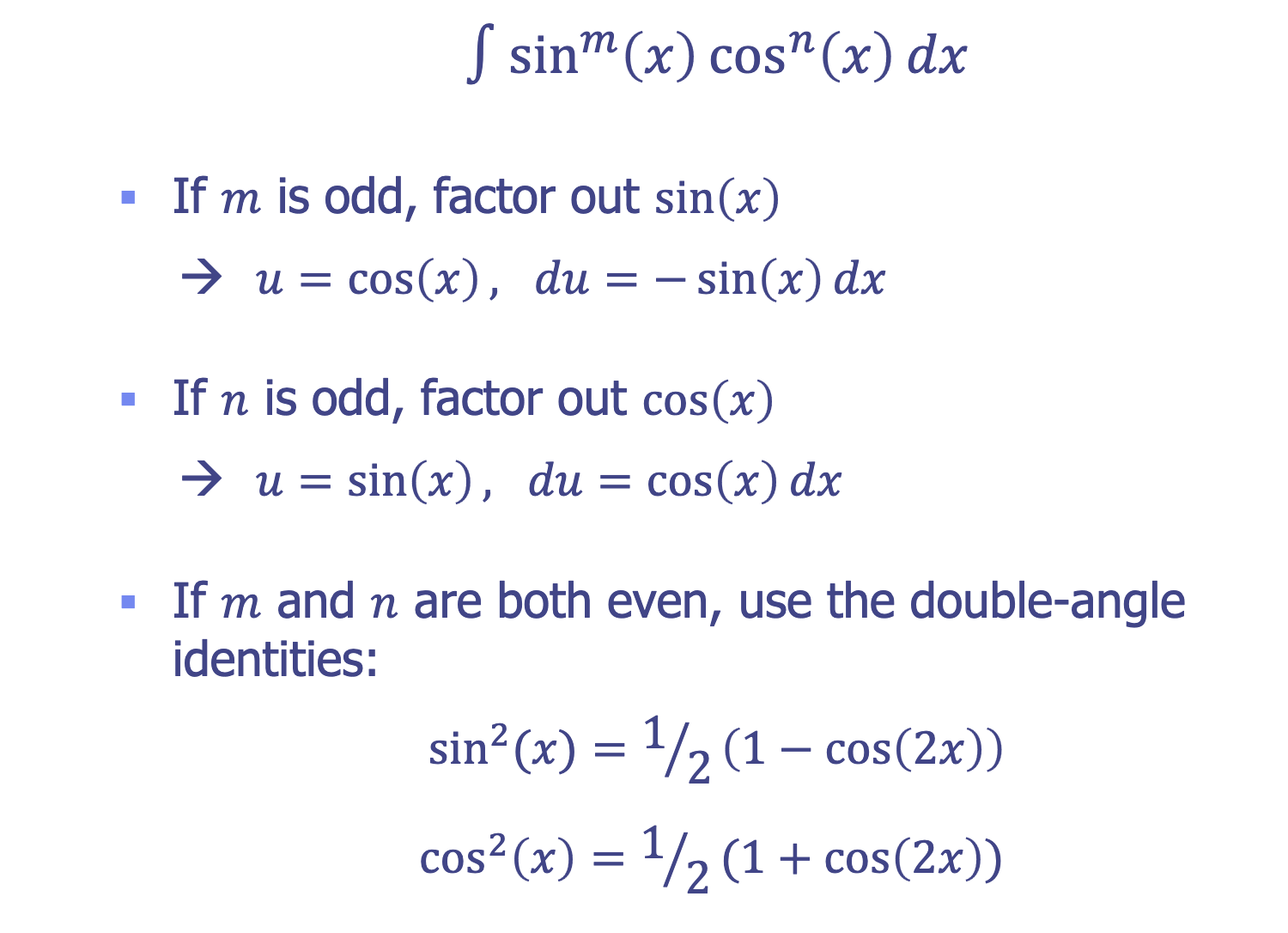
Trigonometric substitutions (to learn)

Integration by parts

Sudv = uv - Svdu

• IBP ends when you’re J integral matches you’re original Sudv, then you can replace as I, get I on one side, and now you have a representation of the og integral w/o other integrals

“dv/dx = sin3x” what is v?

v = -1/3 cos (3x) !!!! integration rule !!!

LIATE (order when choosing which term should be u, in IBP)

1. Ln ,

2. Inverse trig functions,

3. Arithmetic functions (ex: x²),

4. Trig functions,

5. Exponential functions

steps for substitution or “IBP” questions

1. can the problem be solved using only substitution? x can be crossed out?

2. If IBP, then recall LIATE, to find which one should be “u”

3. do the IBP formula and remember that it gets distributed to both terms the definite integral thing.

4. simplify and easy.

antiderivative for e^5x (like when getting v)

versus

derivative for e^5x (over dx)

e^5x = (1/5) e^5x (DIVIDE)

and

e^5x = 5e^5x (MULTIPLY)

integral of secx !!

find it, remember it, and study it !!

Leibniz… to get derivative of anti-derivative

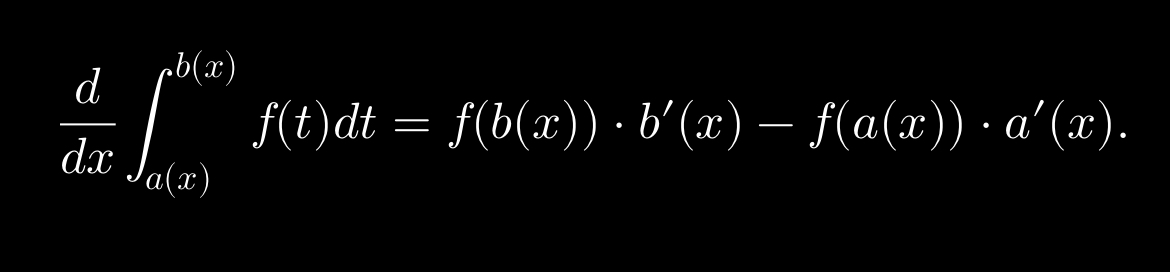
SPLITTING THE INTEGRAL

“arc length” formula