geo H - ch04 - Congruent Triangles

Polygon

A closed plane figure with at least three sides that are segments. The sides intersect only at their endpoints, and no adjacent sides are collinear.

Remote Interior Angles

The angles of a triangle that are not adjacent to a given exterior angle.

Auxiliary Line

A line, ray, or segment added to a diagram to help in a proof.

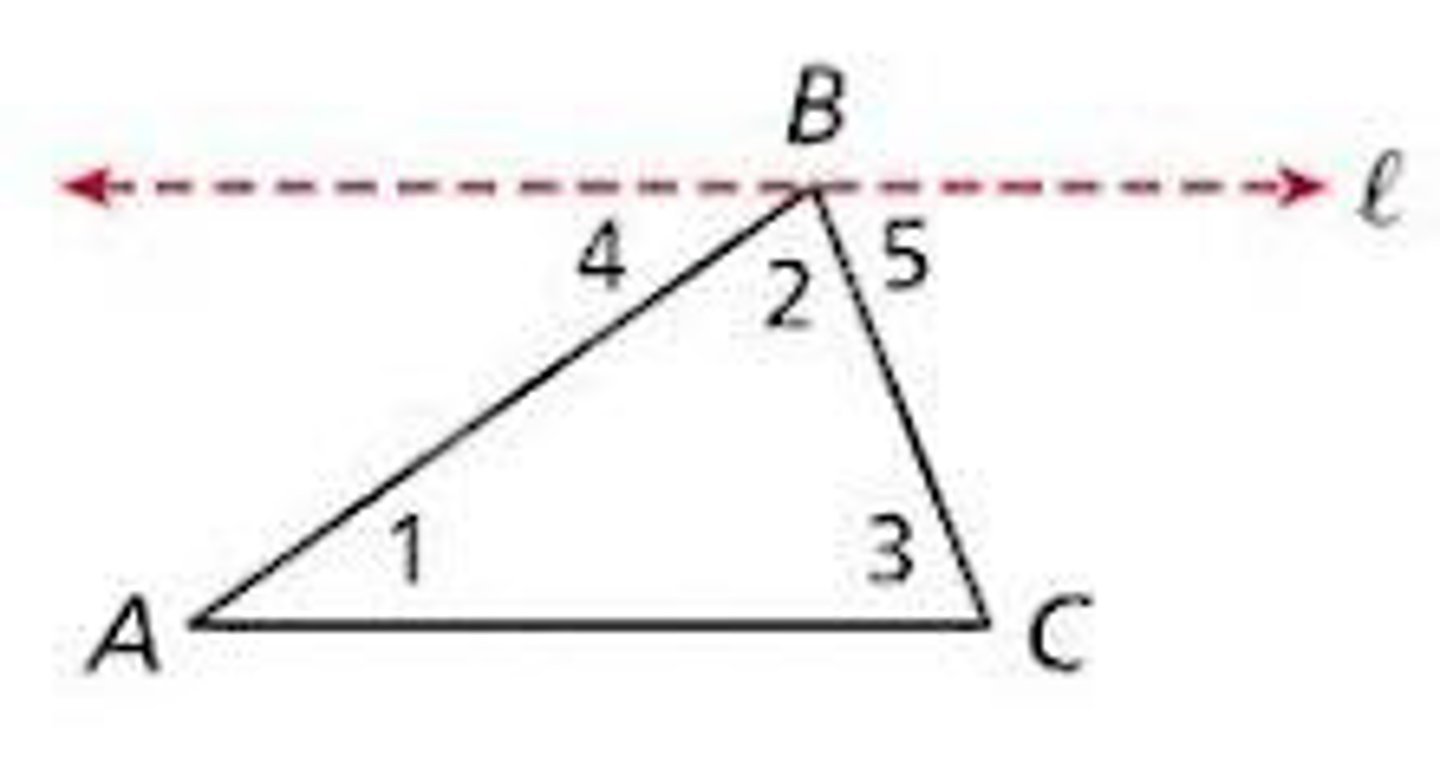
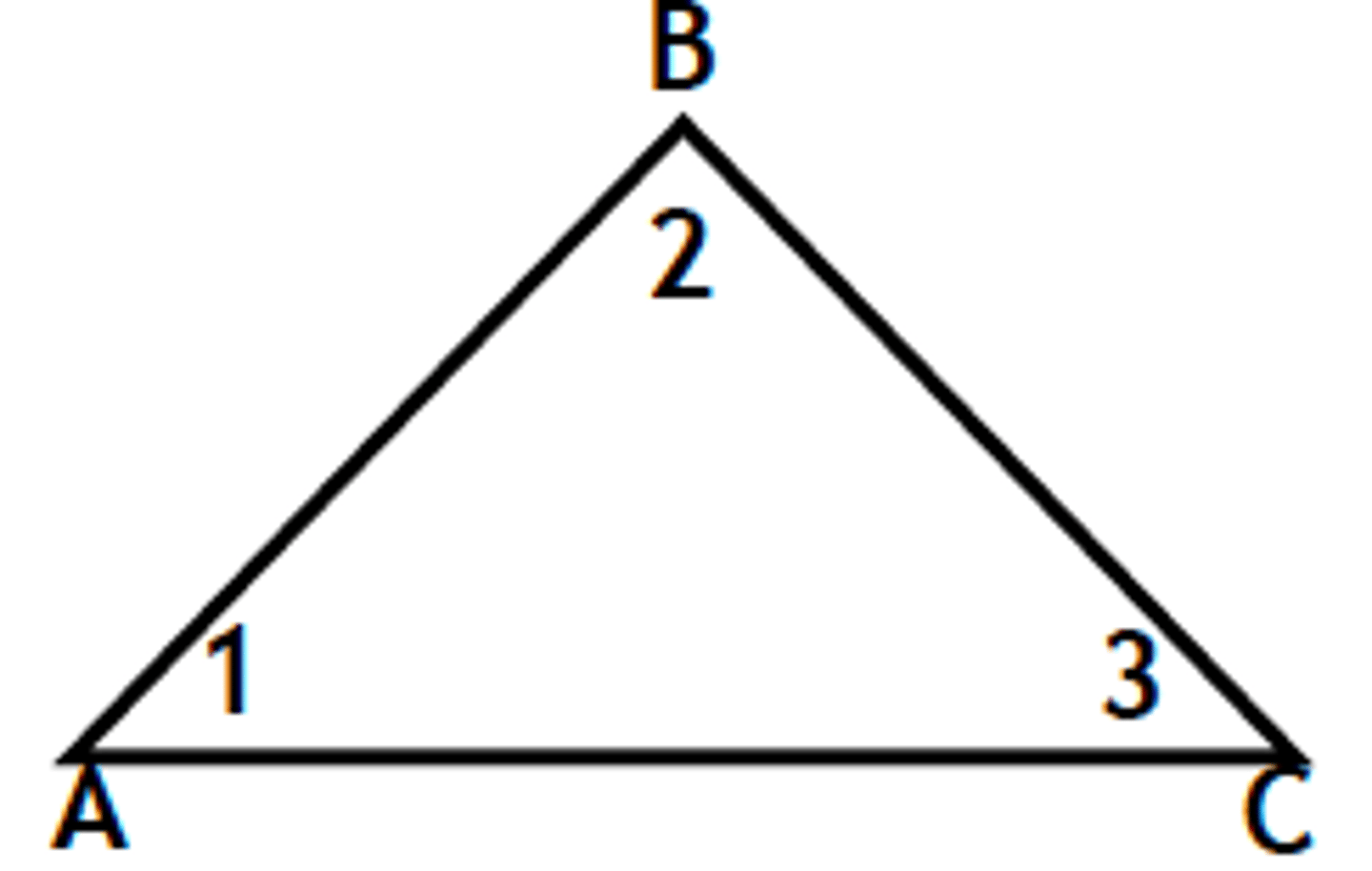
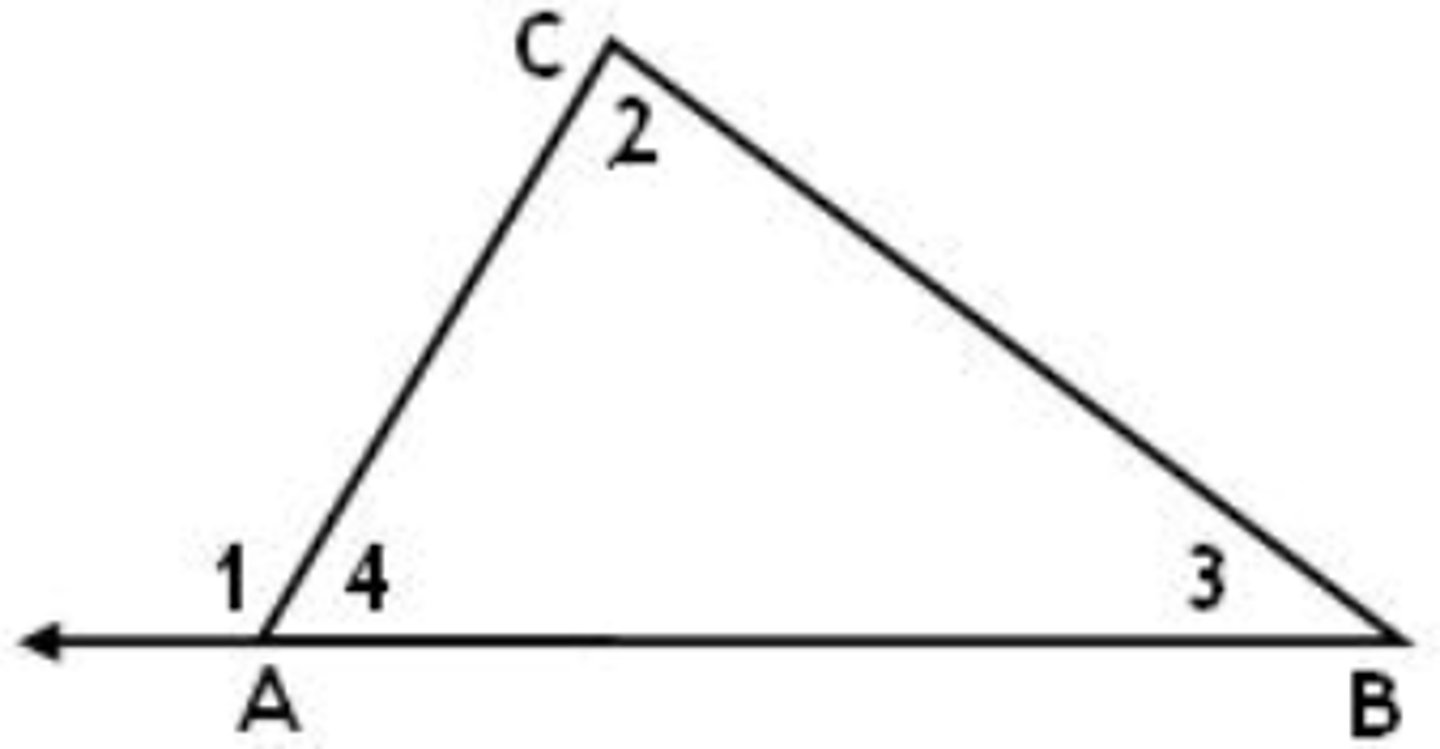
Triangle Angle-Sum Theorem

The sum of the measures of the interior angles of a Δ is 180°.

Given: ΔABC
Prove: m∠1 + m∠2 + m∠3 = 180°

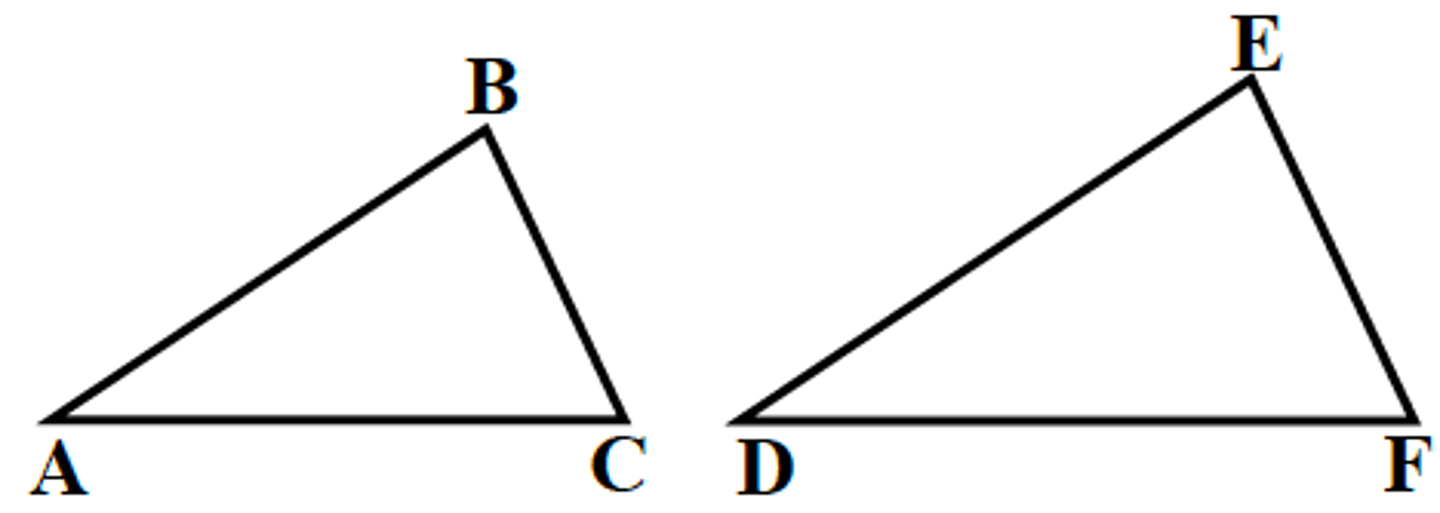
Third Angles Theorem

If two angles of a Δ are congruent to two angles of another Δ,
then the third angles are congruent.

Given: ∠A ≅ ∠D, ∠B ≅ ∠E
Prove: ∠C ≅ ∠F

Acute Triangle

An angle that has three acute angles.

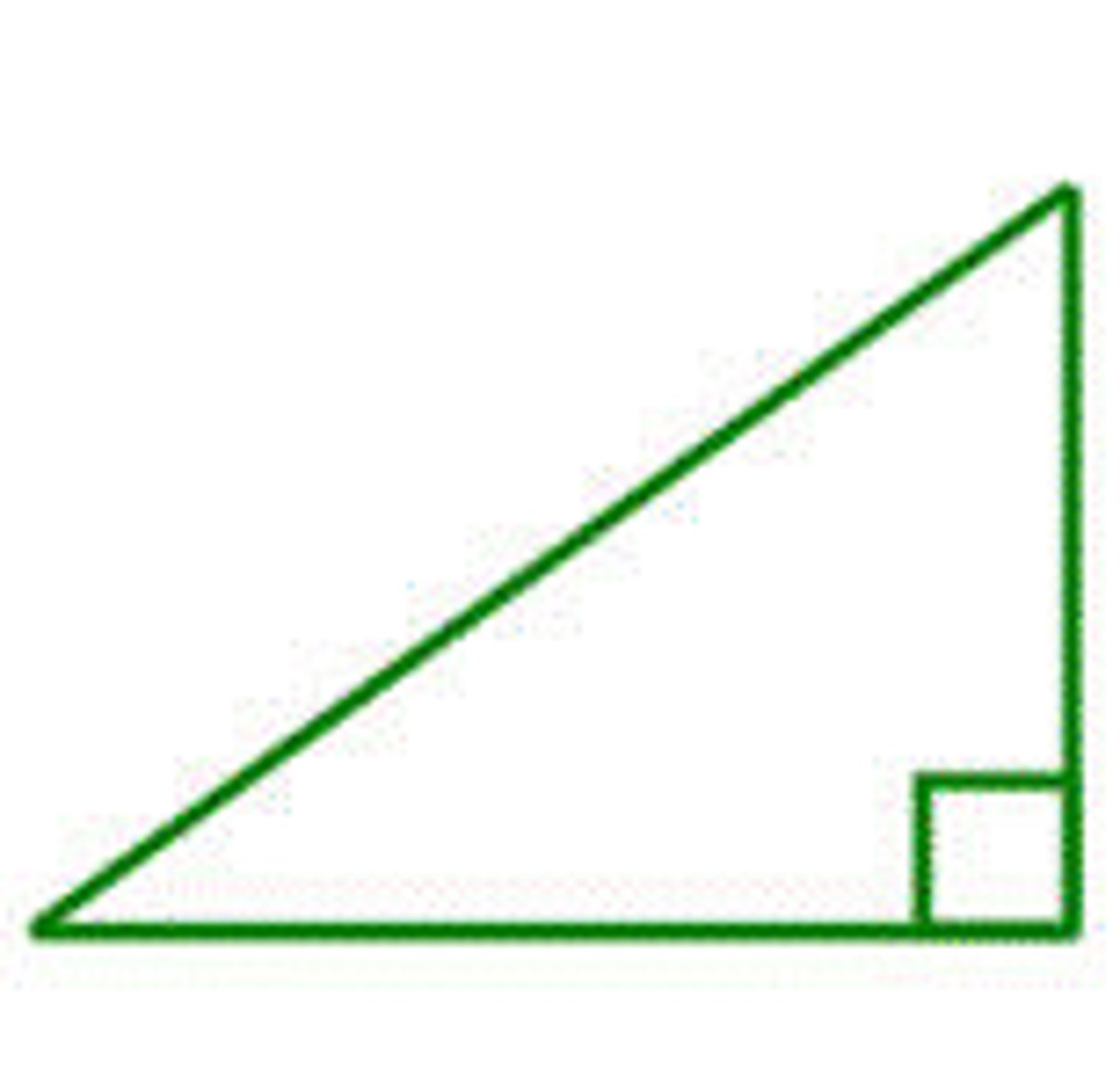
Right Triangle

A triangle that has one right angle.

Obtuse Triangle

A triangle that has one obtuse angle.

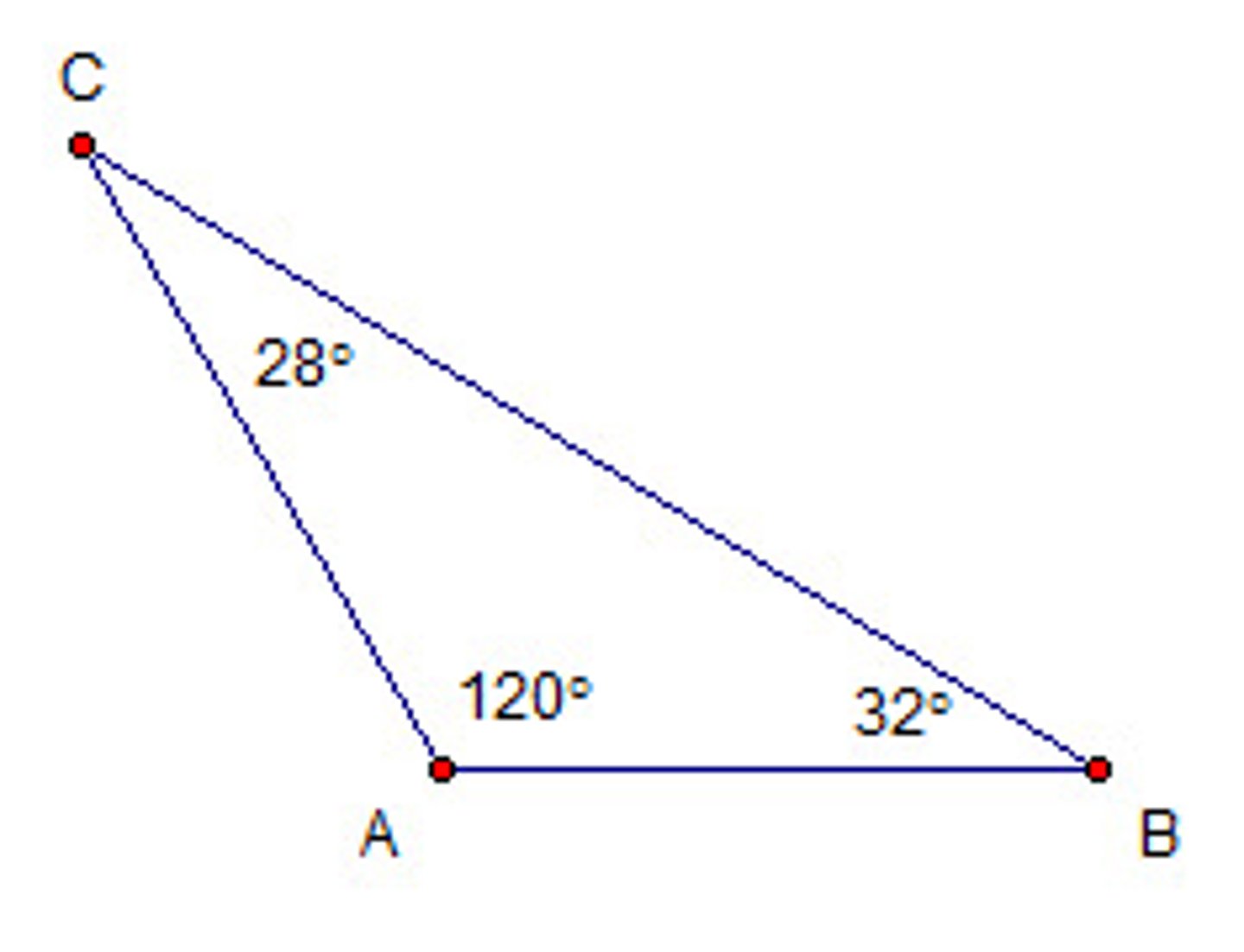
Equiangular Triangle

A triangle that has three congruent angles.

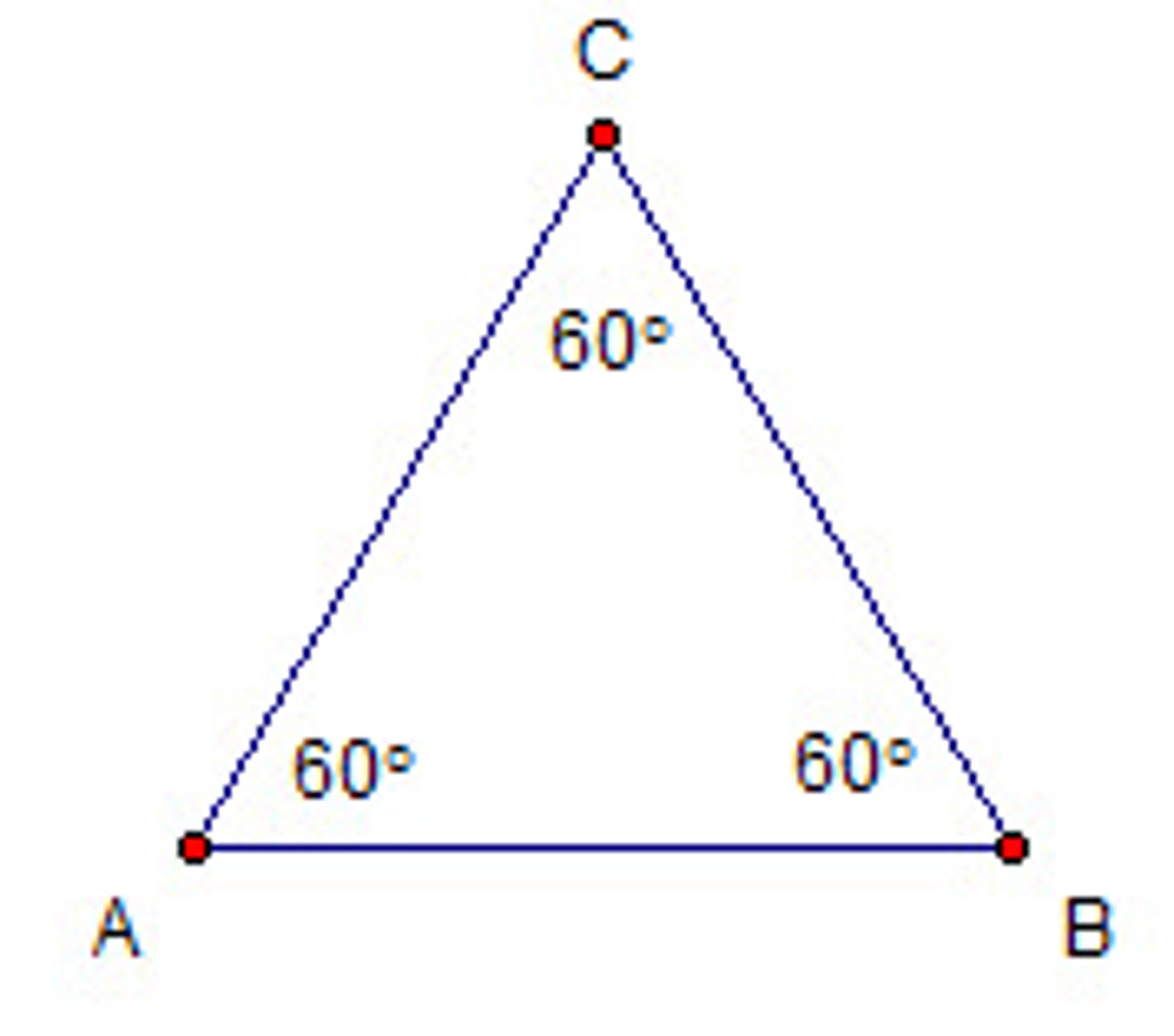
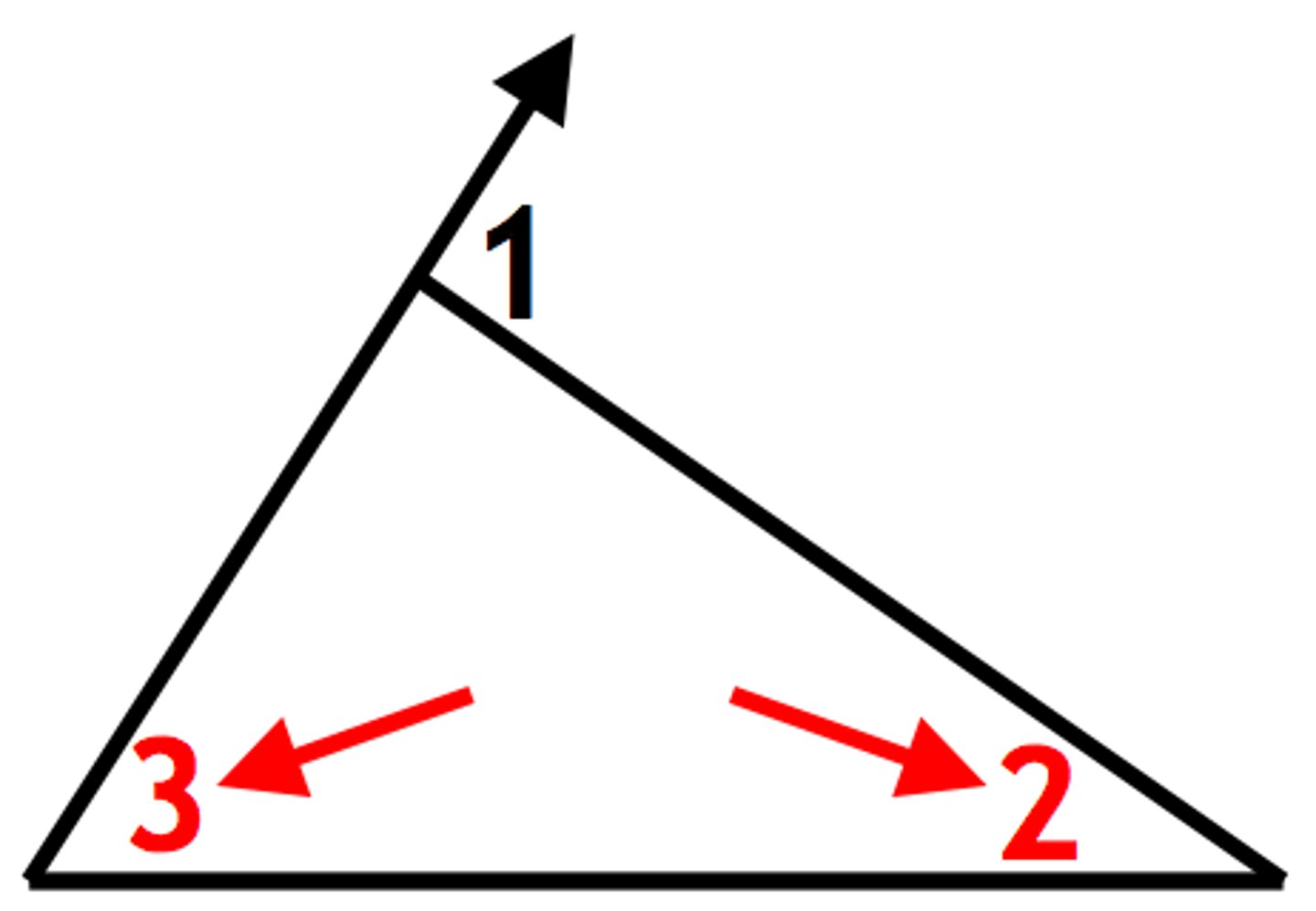
Triangle Exterior Angle Theorem

The measure of an exterior angle of a triangle is equal to the sum of the non-adjacent ("remote") interior angles of the triangle.

Given: ΔABC, exterior angle ∠1
Prove: m∠1 = m∠2 + m∠3

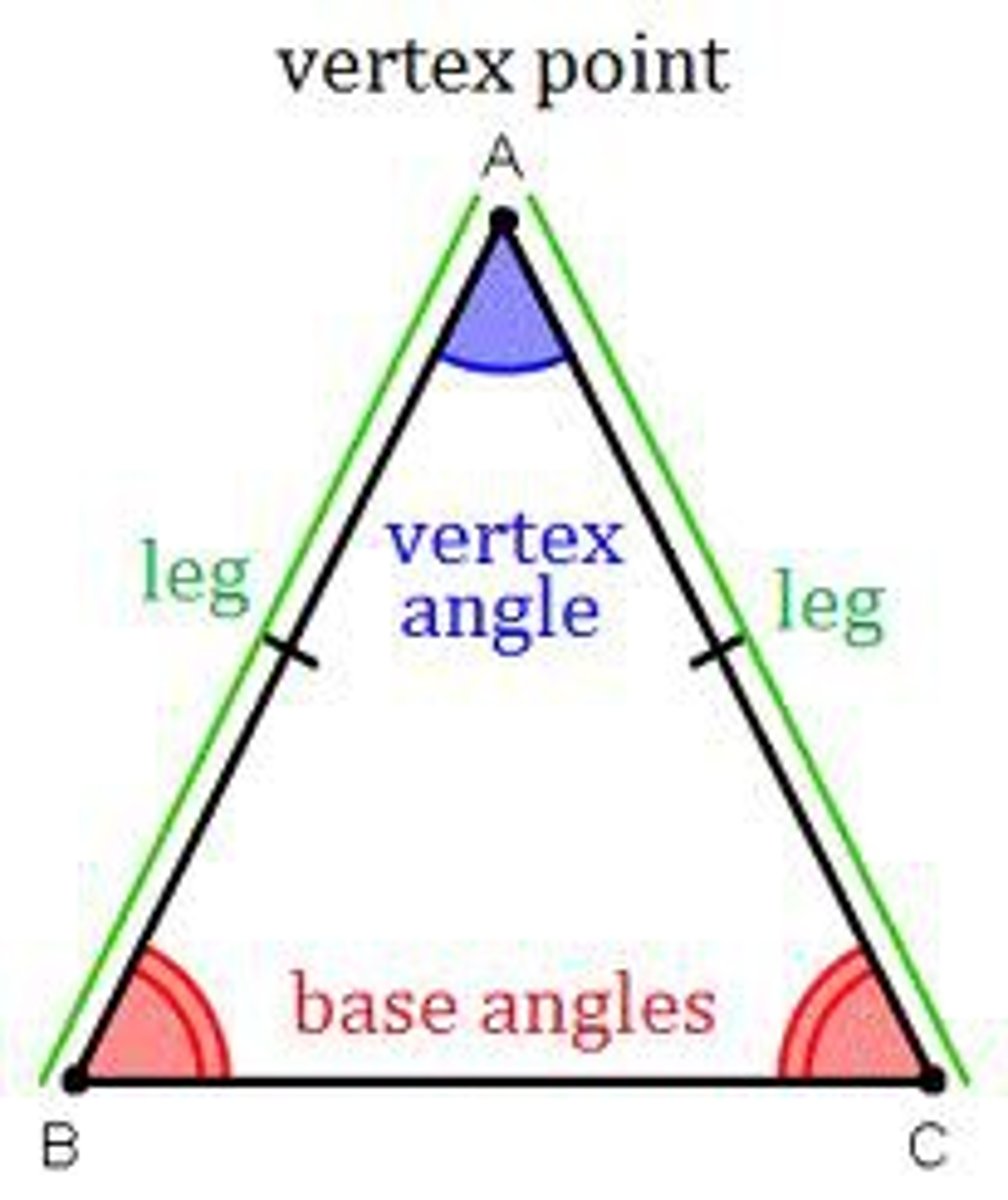
Isosceles Triangle (parts)
1. Legs...
2. Vertex Angle...
3. Base...
4. Base Angles...

1. The congruent sides.
2. The angle formed by the legs.
3. The side opposite the vertex angle.
4. The angles formed by the base and legs.

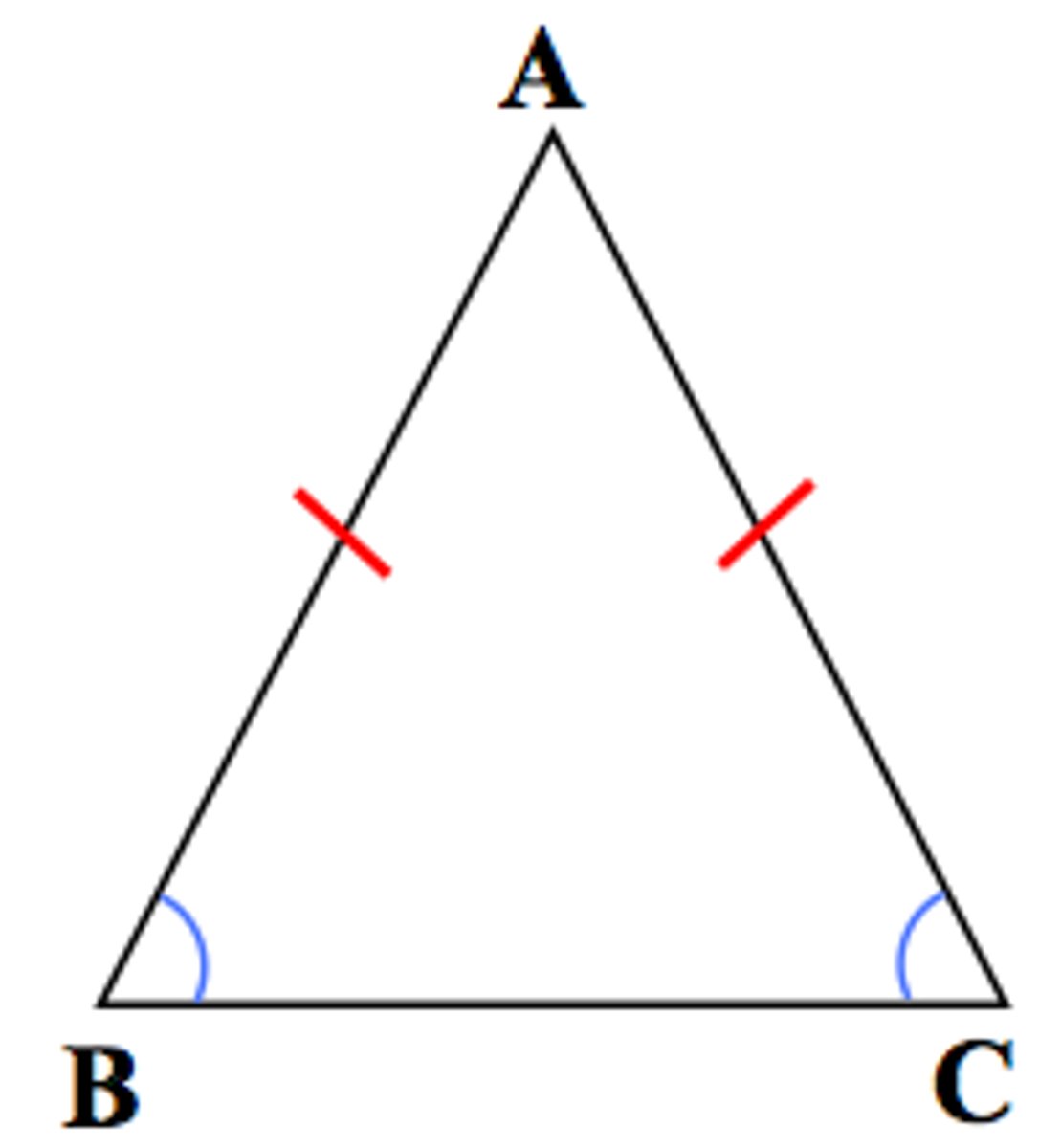
Isosceles Triangle Theorem

If two sides of a Δ are ≅,
then the opposite angles are ≅.

Given: AB ≅ AC
Prove: ∠B ≅ ∠C

Converse of the Isosceles Triangle Theorem

If two angles of a Δ are ≅,
then the opposite sides are ≅.

Given: ∠B ≅ ∠C
Prove: AB ≅ AC

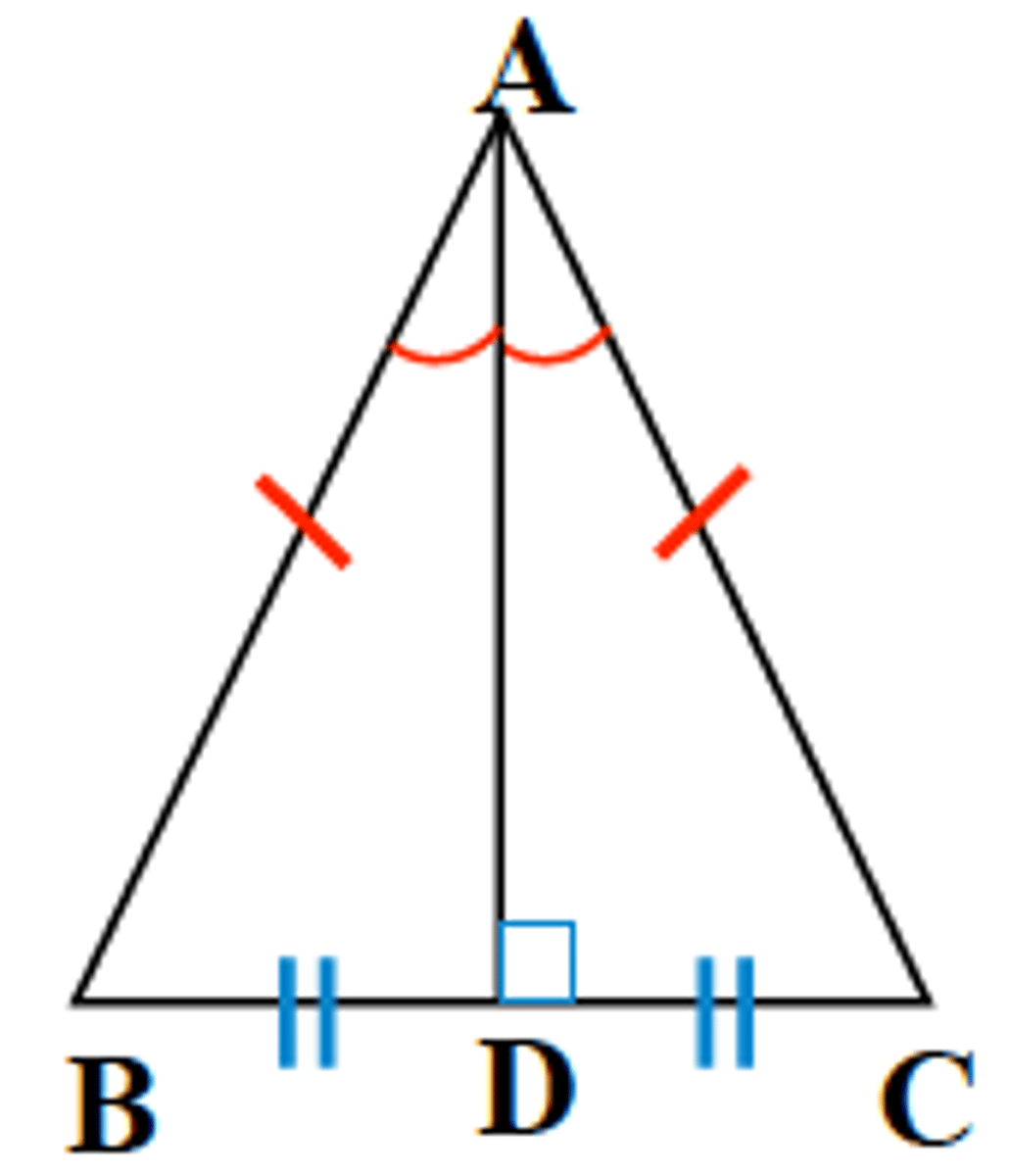
Theorem
The bisector of the vertex angle of an isosceles
triangle is...

... the perpendicular bisector of the base.

Given: AB ≅ AC, AD bisects ∠BAC
Prove: AD is the ⊥ bisector of BC

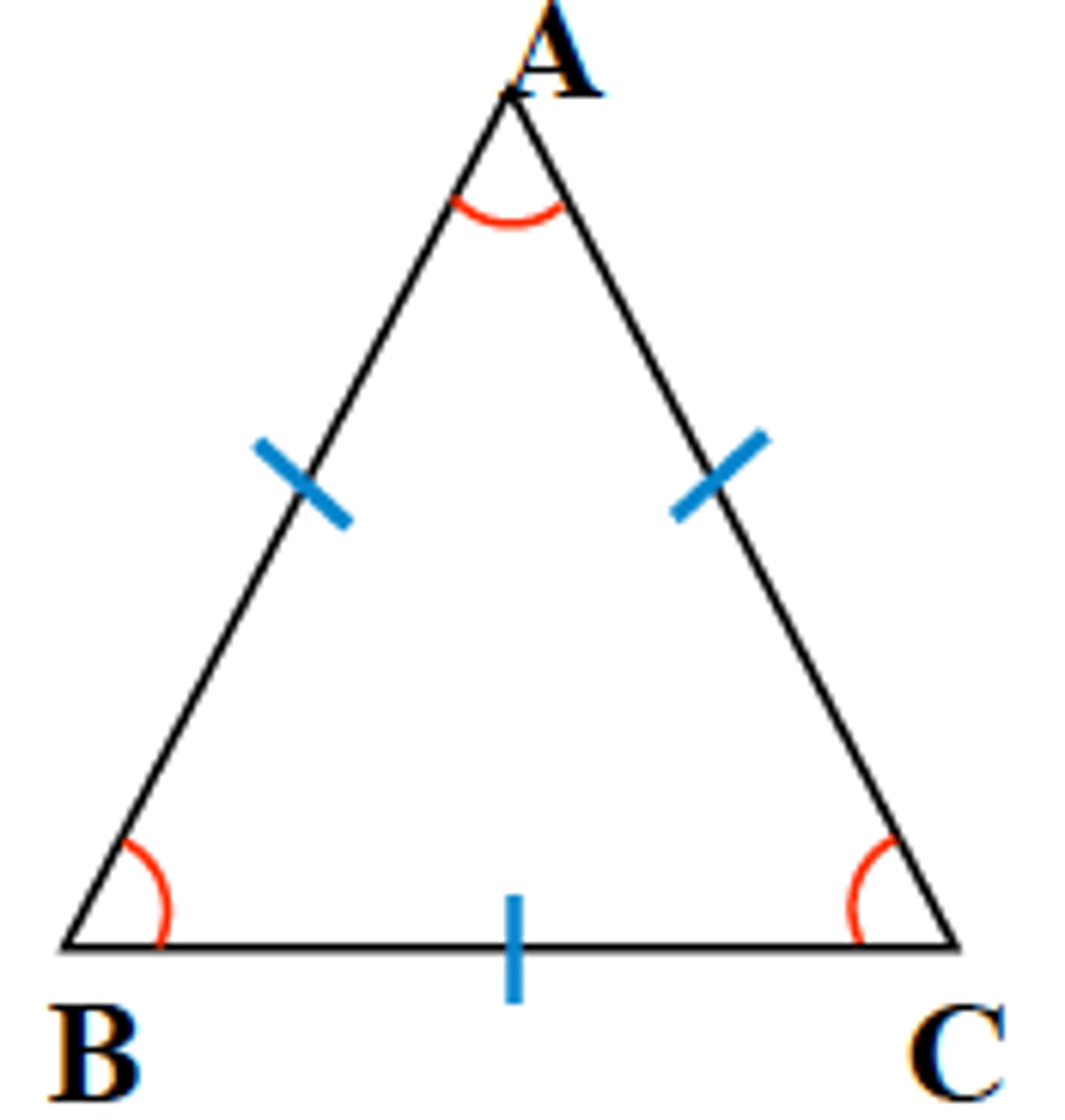
Theorem
If a triangle is equilateral, then the triangle is also....

...equiangular.

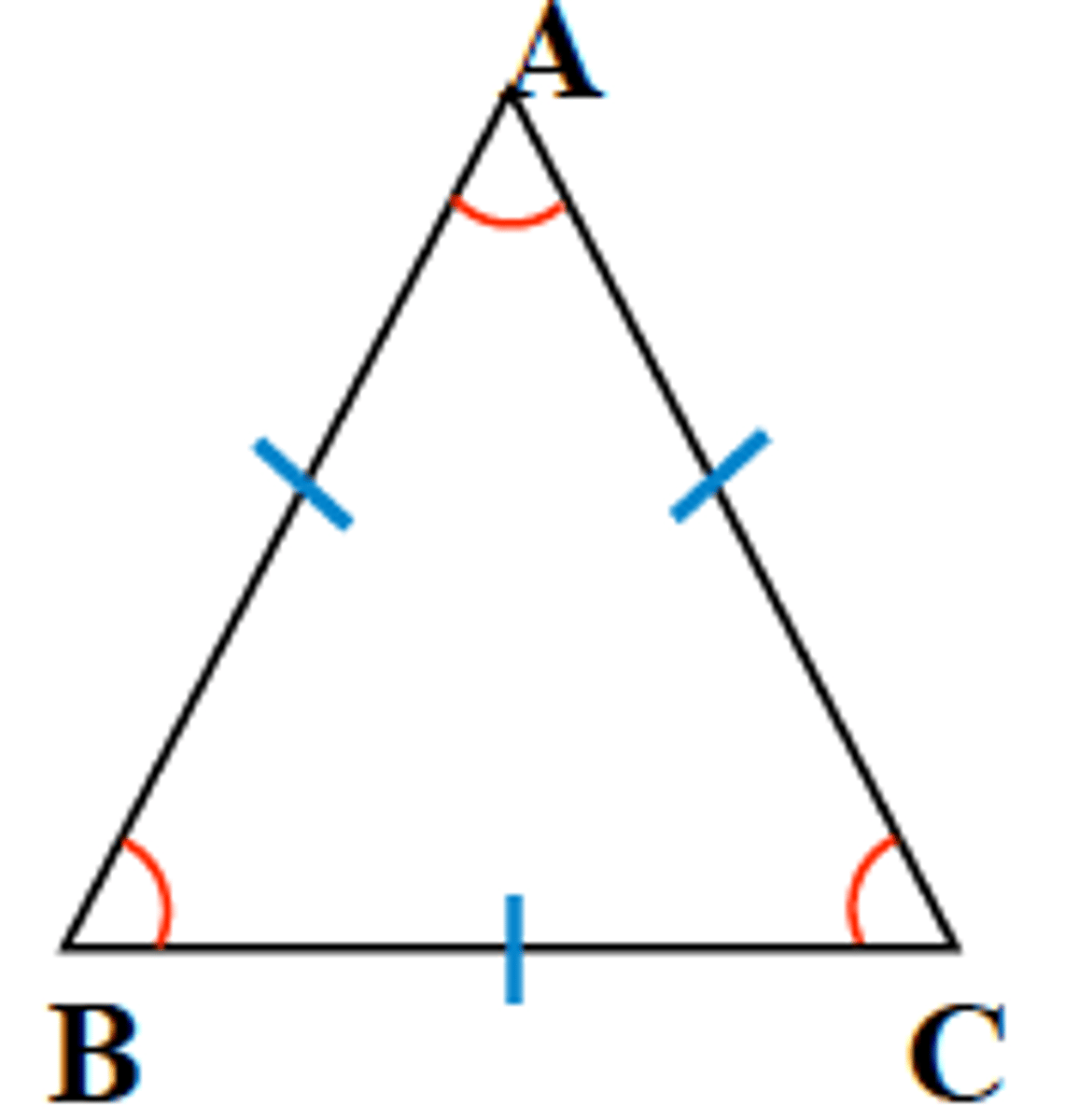
Theorem
If a triangle is equiangular, then the triangle is also...

...equilateral

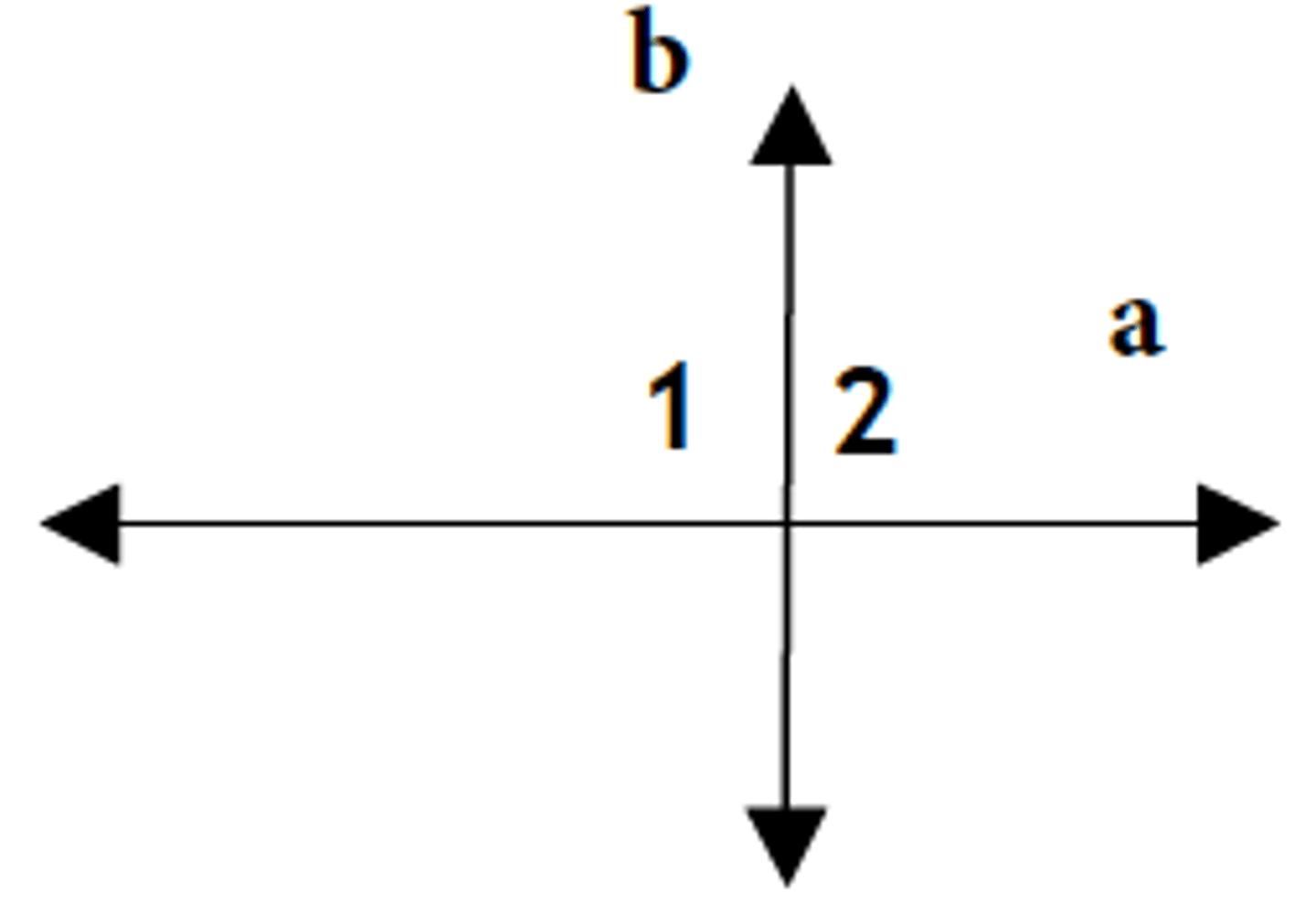
Theorem
If two lines are perpendicular then...

... the lines form congruent adjacent angles.

Given: a ⊥ b
Prove: ∠1 ≅ ∠2

Theorem
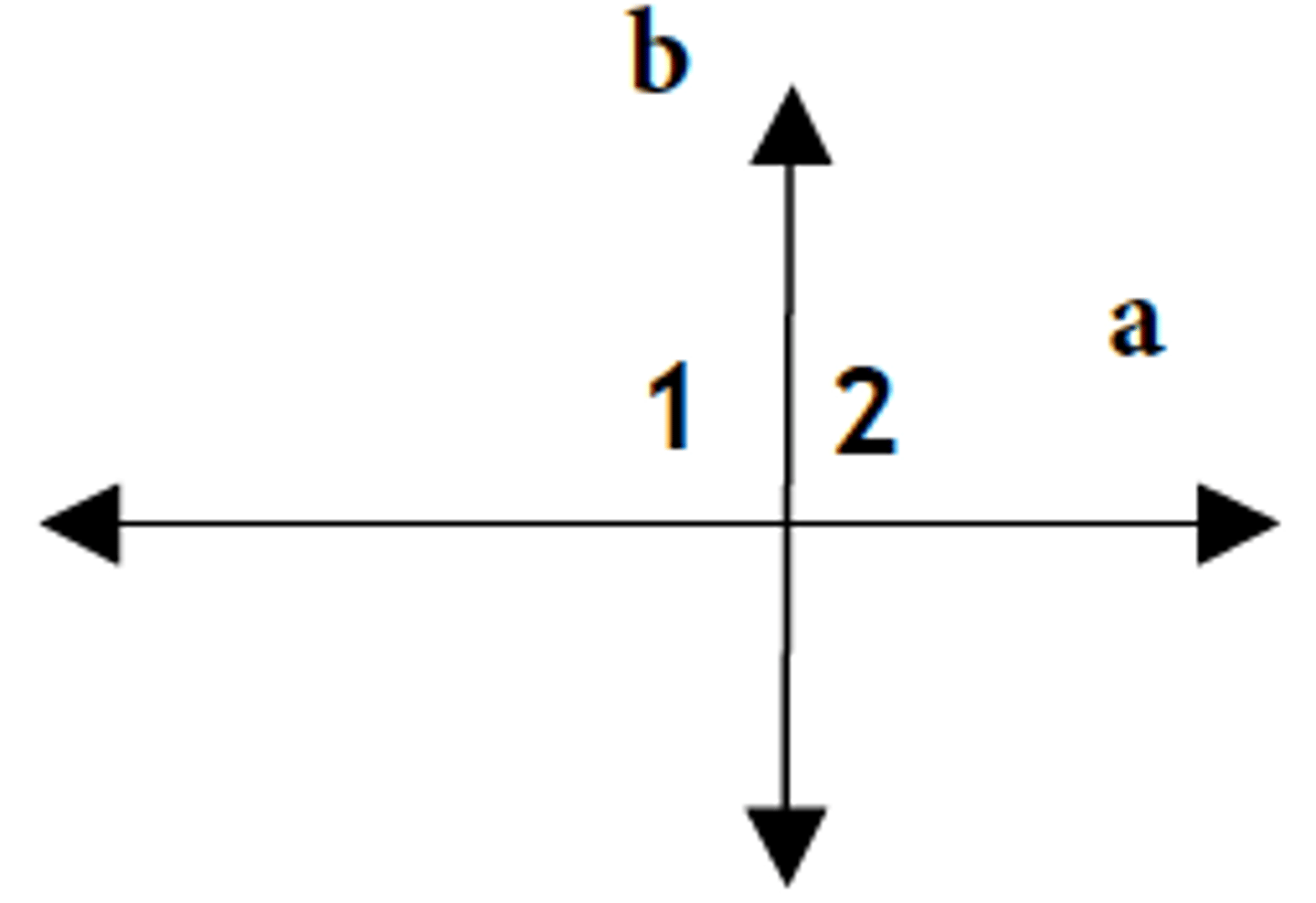
If two lines form congruent adjacent angles, then...

....then the lines are perpendicular.

Given: diagram, ∠1 ≅ ∠2
Prove: a ⊥ b

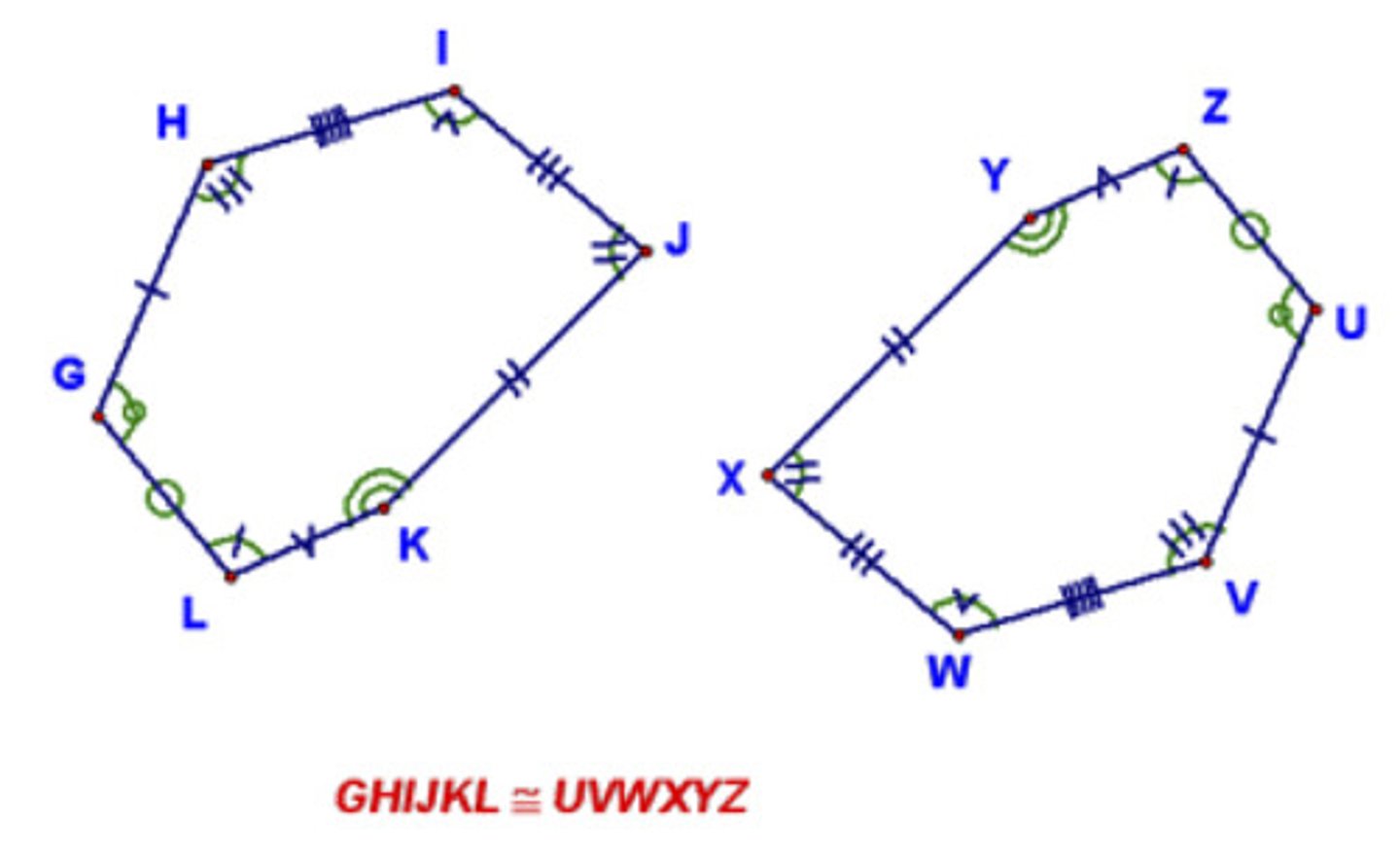
Congruent Polygons

Polygons with:
1. corresponding sides that are congruent
2. corresponding angles that are congruent

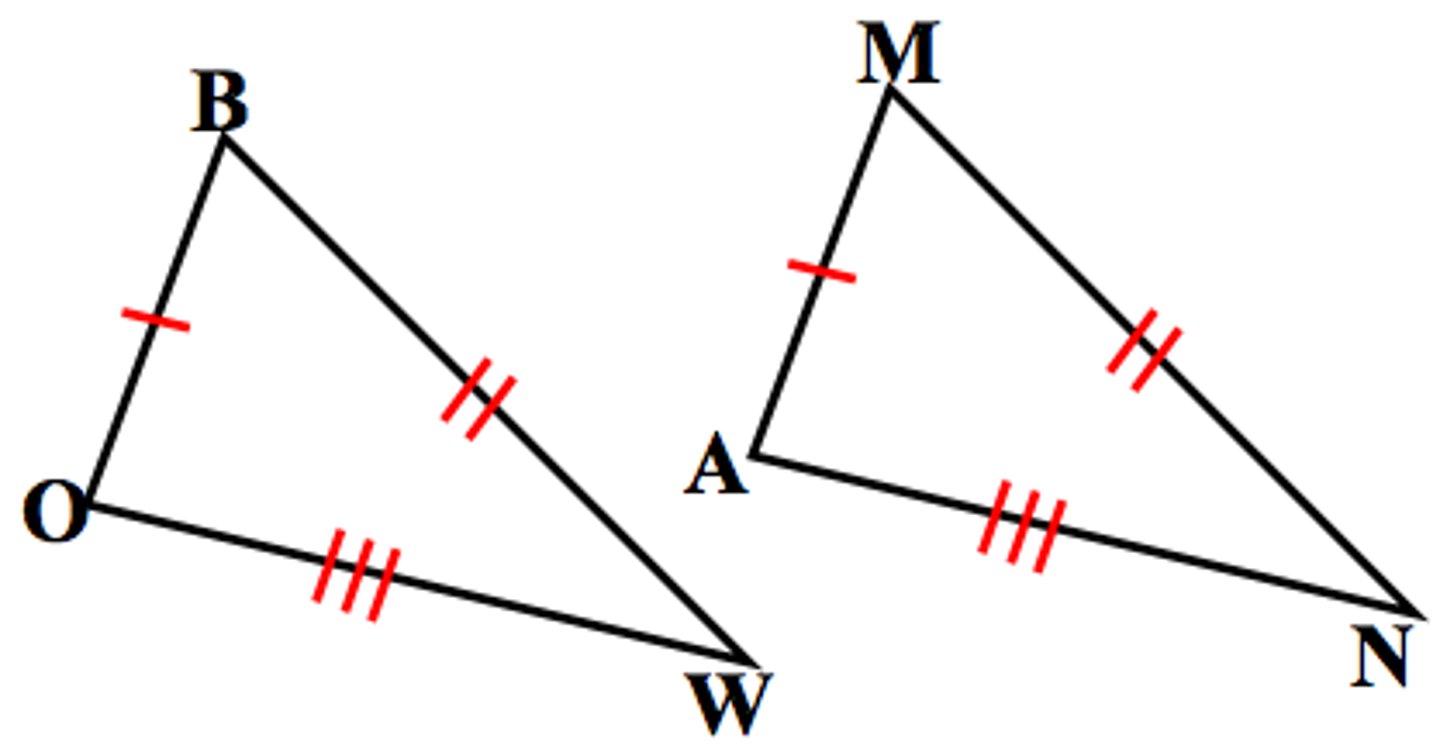
Side-Side-Side Theorem (SSS)

If the three sides of one triangle are congruent to the three sides of another triangle,
then the two triangles are congruent.

Given: BO ≅ MA , OW ≅ AN , BW ≅ MN
Prove: ΔBOW ≅ ΔMAN

Side-Angle-Side Theorem (SAS)

If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle,
then the two triangles are congruent.

Given: 𝐵𝑂 ≅ 𝑀𝐴 , 𝑂𝑊 ≅ 𝐴𝑁 , ∠O ≅ ∠A
Prove: ΔBOW ≅ ΔMAN

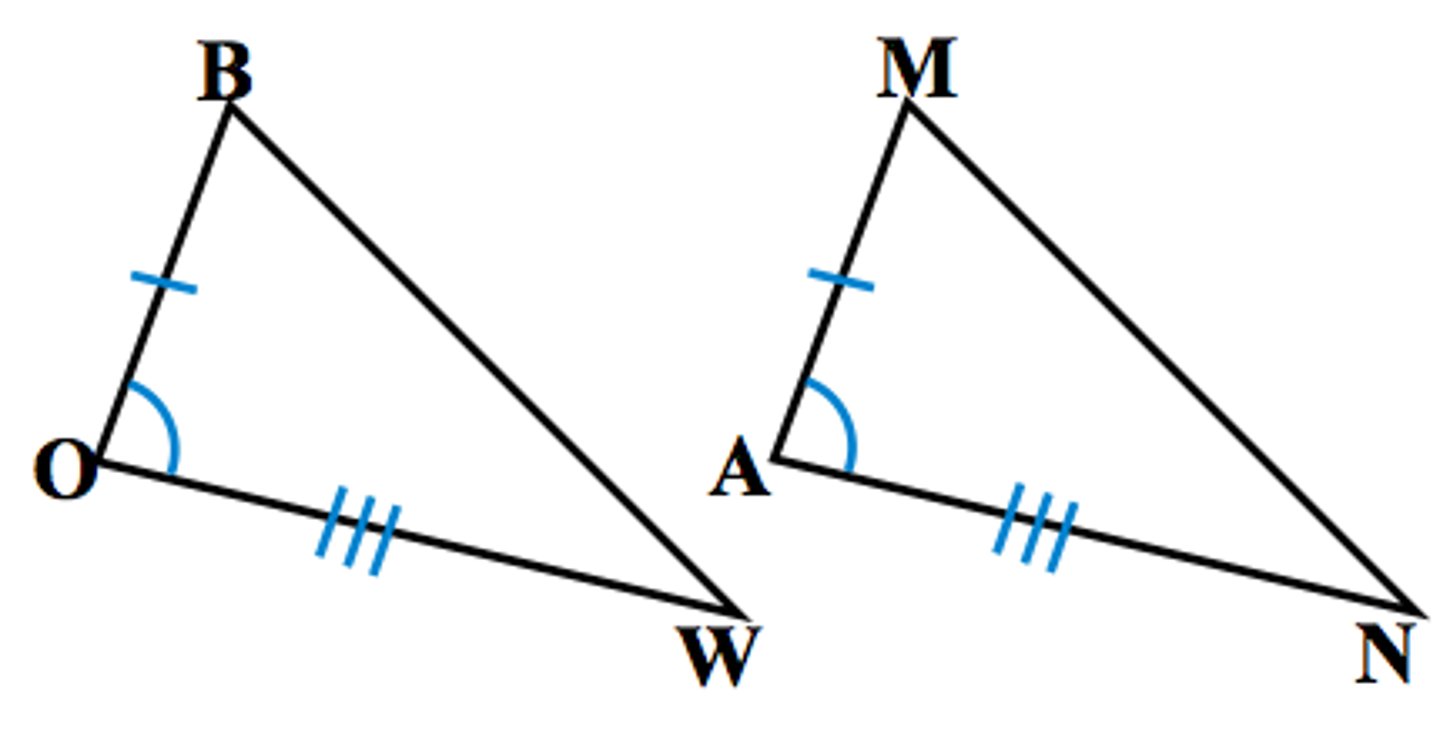
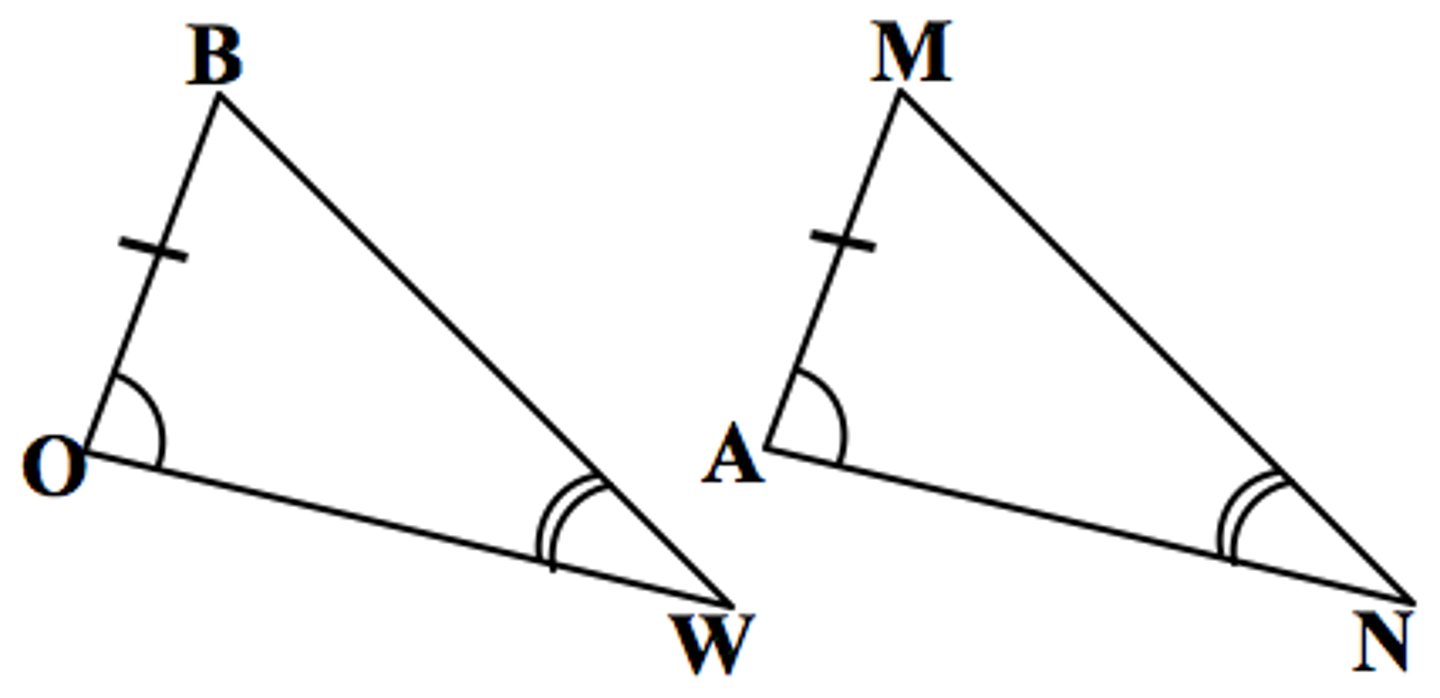
Angle-Side-Angle Postulate (ASA)

If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle,
then the two triangles are congruent.

Given: ∠O ≅ ∠A, OW ≅ AN, ∠W ≅ ∠N

Prove: ∆BOW ≅ ∆MAN

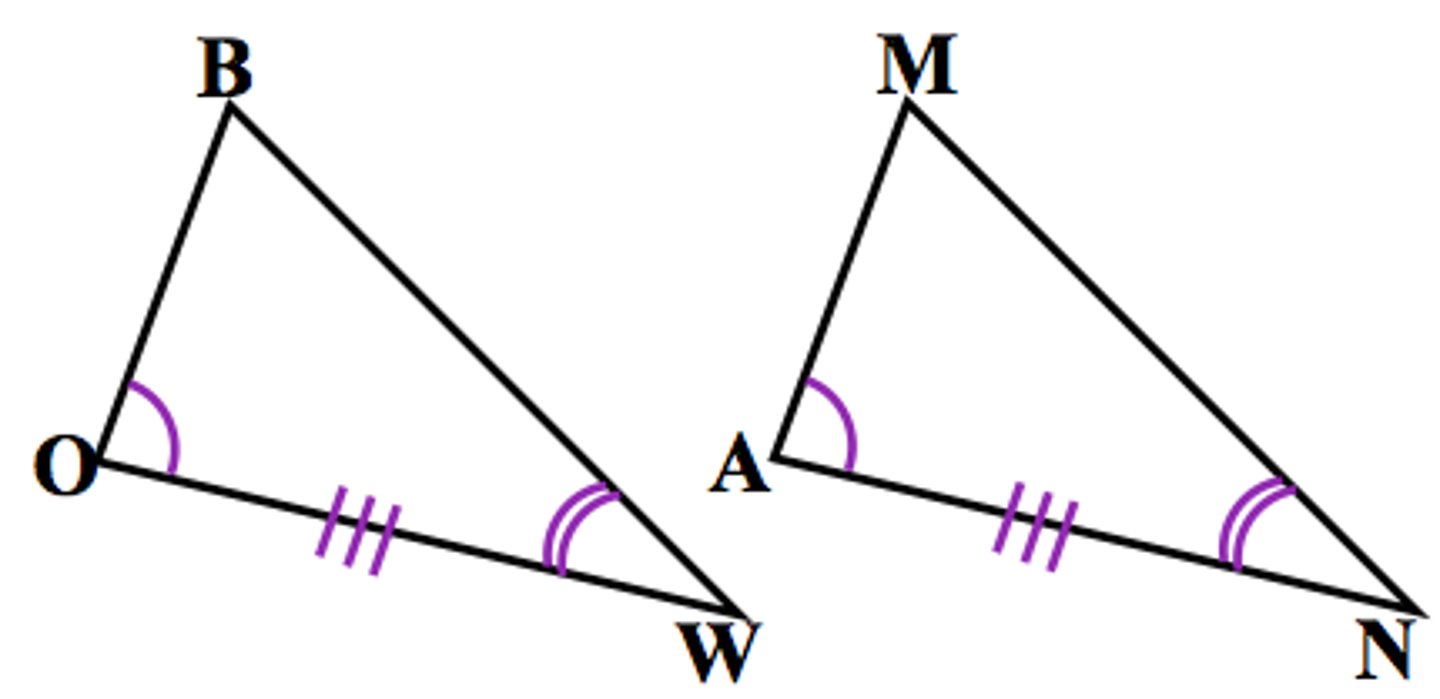
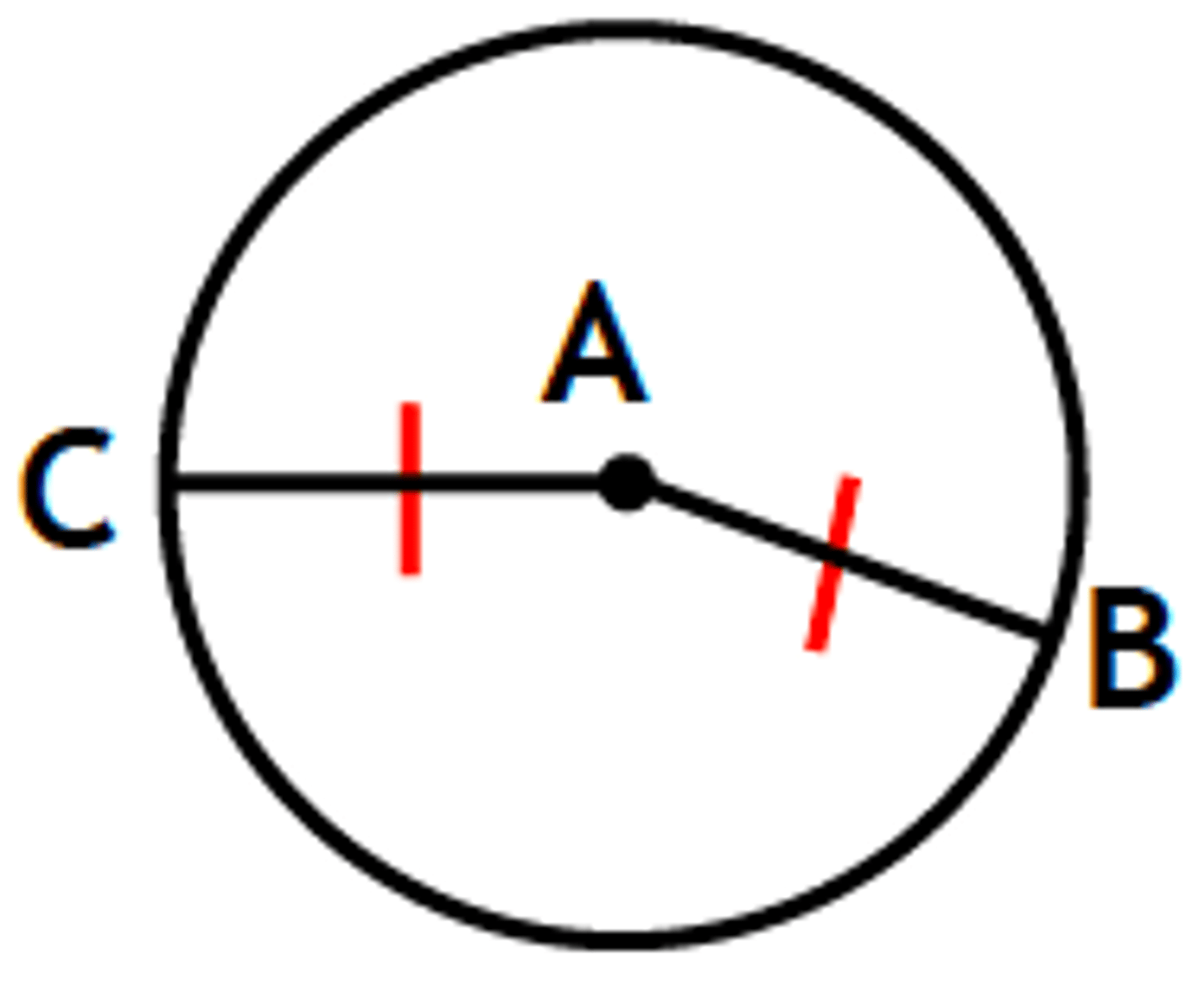
Theorem
All radii of a circle are congruent.

Given: circle A, diagram
Prove: AB ≅ AC

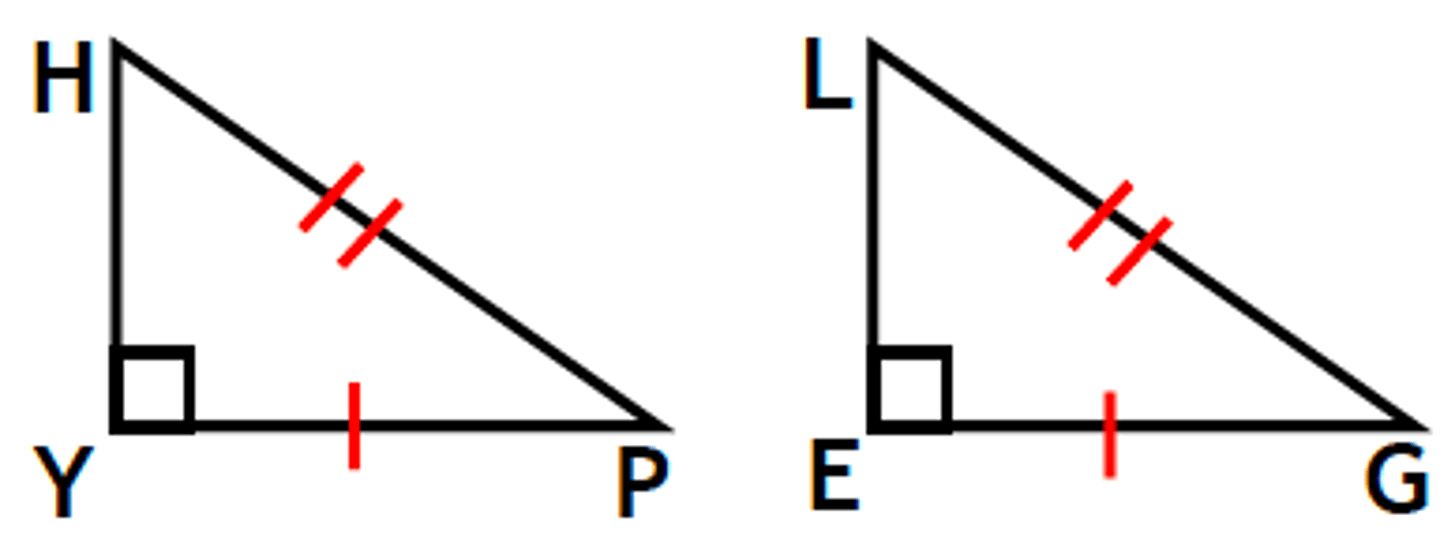
Hypotenuse-Leg Theorem (HL)

If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of another right triangle,
then the triangles are congruent.

Given: ΔHYP is a right Δ, ΔLEG is a right Δ, 𝑌𝑃 ≅ 𝐸𝐺,𝐻𝑃 ≅ 𝐿𝐺
Prove: ΔHYP ≅ ΔLEG

Angle- Angle-Side Theorem (AAS)

If two angles and the non-included side of one triangle are congruent to two angles and the non-included side of another triangle,
then the two triangles are congruent.

Corresponding parts of congruent triangles are congruent (CPCTC) does prove...

(CPCTC) does prove that the corresponding parts of congruent triangles are congruent.

Corresponding parts of congruent triangles are congruent (CPCTC) does NOT prove...

CPCTC does NOT prove that triangles are congruent.

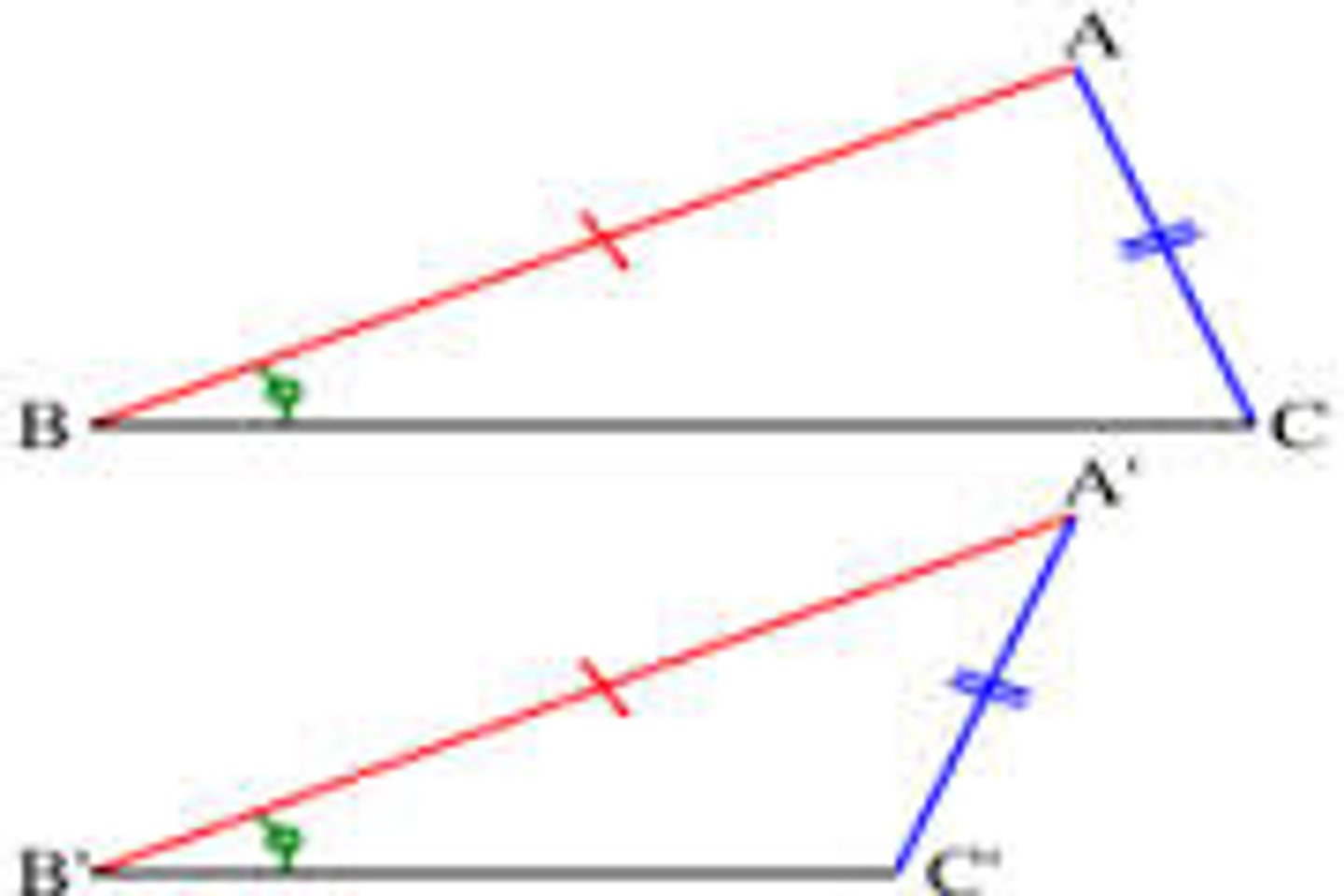
Side-Side-Angle (SSA)

Does NOT prove that triangles are congruent!

Angle-Angle-Angle (AAA)

Does NOT prove that triangles are congruent!