Trig and log derivatives test

All the trig identities and fundemental limits one would need!

fundamental sin limit

lim as x approaches 0 of sinx over x (or the inveerse) is 1

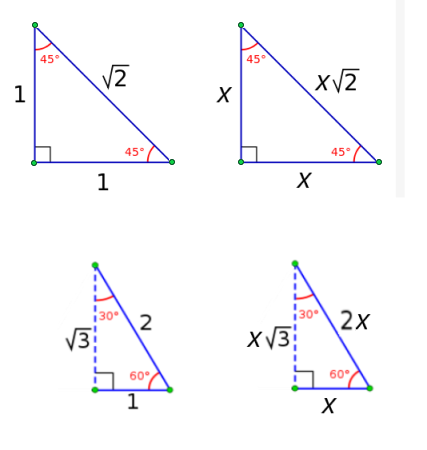
Special triangles

derivative of sinx

=cosx

dy/dx (cosx)

=-sinx

dy/dx (tanx)

=sec²(x)

dy/dx(secx)

=tanxsecx

dy/dx(cotx)

=-csc²x

dy/dx (cscx)

=-cscxcotx

e=

limit as x approaches 0 of (1+x)^1/x or limit as n approaches infinity of (1+1/n)^n

dy/dx (e^x)

=e^x

dy/dx (lnx)

= 1/x

exponential growth or decay function

f(t) = ce^kt where c = initial population, t= time and k = growth/decay factor

pythagorean trig identities

cos²x + sin²x = 1
1 + tan²x = sec²x

1 + cot²x = csc²x

quotient identities

tanx = sinx/cosx
cotx = cosx/sinx

sin (x+y)=

sinxcosy + sinycosx

sin (x-y)=

sinxcosy - sinycosx

cos (x+y)=

cosxcosy - sinxsiny

cos (x-y) =

cosxcosy + sinxsiny

sin2x =

2sinxcosx

cos2x =

cos² x - sin²x
1-2sin²x
2cos²x - 1

sin (pi/2 - x)=

cosx

cos (pi/2 - x)=

sinx

tan (pi/2 - x)

= cotx