Circular Motion

NB: Do all calculations in Radians for this topic

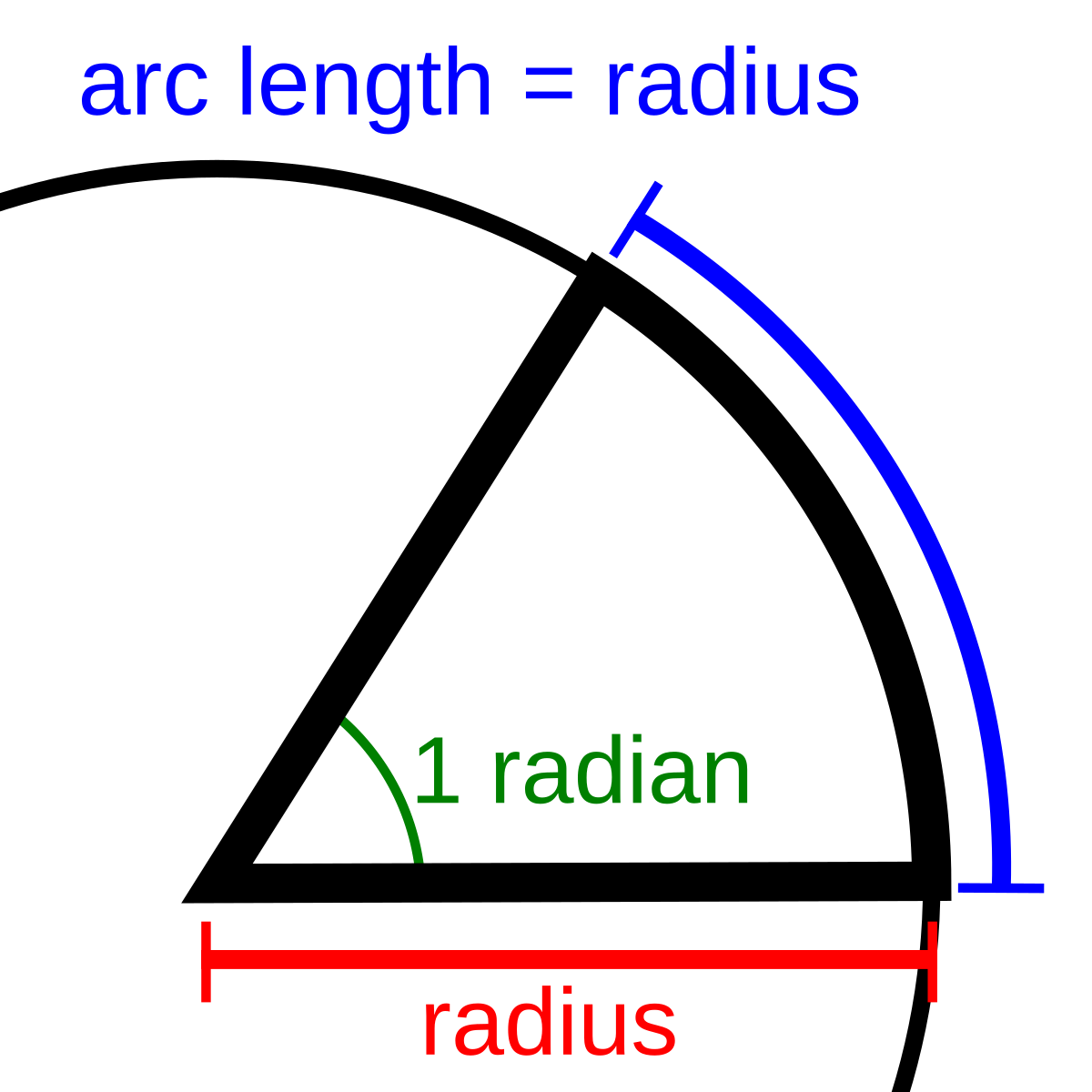
How is the radian defined?

Include a diagram

• The angle subtended by a circular arc with a length equal to the radius of the circle

• angle in radians = arc length/ radius

How many radians are in 360°?

2π radians

How do you convert from degrees to radians?

angle in degrees ° X π/180

How do you convert from radians to degrees?

angle in radians radians X 180/ π

How is angular velocity defined?

The angular velocity (ω) of an object moving in a circular path is defined as the rate of change of angle. Therefore

ω = θ(angle)/ t(time)

In a time t, equal to 1 time period (T), the object will move through an angle equal to 2π radians → ω = 2π/ T

How can angular velocity be calculated with an angle and time?

ω = θ(angle)/ t(time)

What are the units of angular velocity?

rads^-1

What is meant by Time period (T), in circular motion and what are the units?

The time it takes to complete one complete circle (2π radians)

Seconds

What is meant by frequency?

The number of revolutions/rotations per second

How are frequency and Time period related?

Include units for frequency

Frequency is the reciprocal of the Time period

f= 1/T

Hz

How are angular velocity and time period related?

ω=2π/T

How are angular velocity and frequency related?

ω= 2πf

State Newton’s first law?

Any accelerating object requires a net (resultant) force to be acting on it.

Any force that keeps a body moving with a uniform speed along a circular path is called a centripetal force

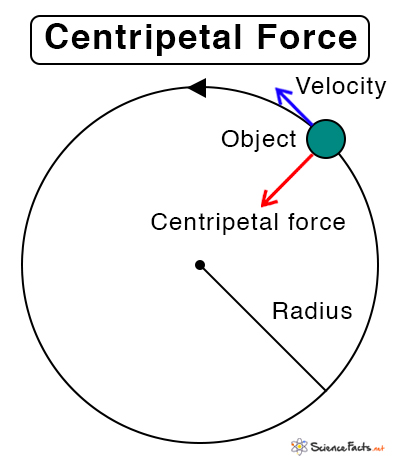
What is meant by circular motion?

An object is moving in a circular path at a constant speed due to a force acting towards the centre of the circle

Why does circular motion occur?

Include a diagram

• A centripetal force is any force that keeps a body moving with a uniform speed along a circular path

• A centripetal force is always perpendicular (90°) to the velocity of the object.

• This means that this force has no component in the direction of motion and so no work is done on the object

• As a result the speed remains constant

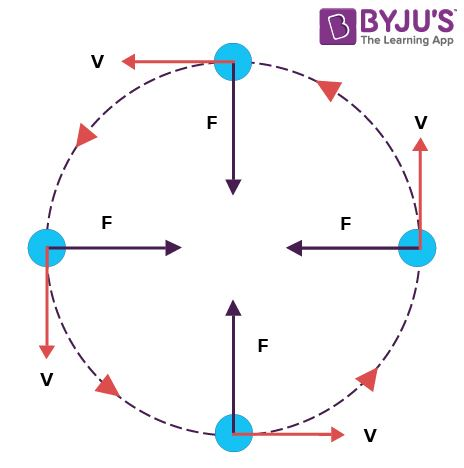
Explain why an object travelling in a circle at a constant speed is accelerating?

• When you move in a circular path, your direction is continuously changing

• As a result your velocity is changing even if you are travelling at a constant speed

• This change in velocity means that objects following a circular path must be accelerating

• Greater rate of change of velocity means greater the acceleration

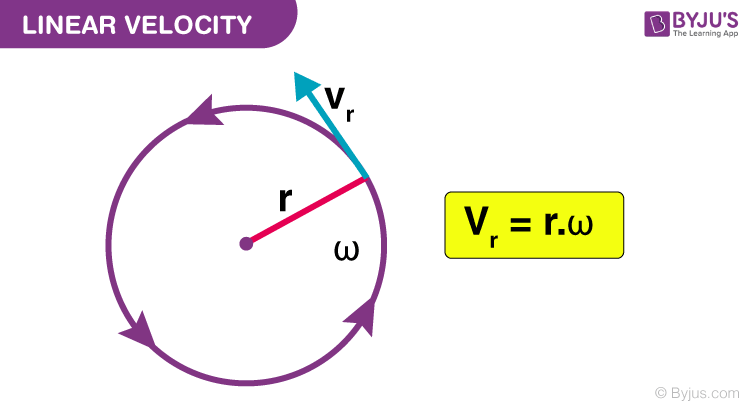
What is the difference between angular velocity and linear velocity (speed) in circular motion?

• Linear velocity is always at a tangent to the circular path (90° to the radius).

  • For an object at constant speed we can use speed = distance travelled/ Time taken

• Angular velocity is the distance travelled of the circumference of the circle and time is the time period

  • We can use v= 2πr/T

How is angular velocity and linear speed related?

v= 2πr/T → Since ω=2π/T →

v=r ω

What is centripetal acceleration, and which direction does it act in?

The acceleration of any object travelling in a circular path at a constant speed.

Acts towards the centre of the circle (same as the centripetal force)

a=v²/r →

v=ωr - v² = ω² r² →

a= ω² r²/ r → a= ω²r

State 2 equations for centripetal acceleration?

Define all terms

• a=v²/r

  • Centripetal acceleration= velocity² / radius

• a= ω²r

  • Centripetal acceleration= angular velocity² X radius

In what direction does centripetal force act and what is the equation for it?

Towards the centre of the circle

F= mv²/r

Centripetal Force= Mass X Velocity² / Radius

How do you derive for F= mv²/r (Centripetal Force)?

Combine F=ma with a= v²/r → F= mv²/r

How are you able to calculate Centripetal force in terms of angular velocity?

F is directly proportional to v², since v=ωr, centripetal force can be written in terms of angular velocity

F=mrω²

Centripetal force= Mass X Radius X Angular Velocity²

Give one example of a circular motion and state the source of the centripetal force?

A car is approaching a bend and must slow down in order to ensure the maximum frictional force between the tyres and the road is sufficient to provide the required centripetal force

Friction= Centripetal force

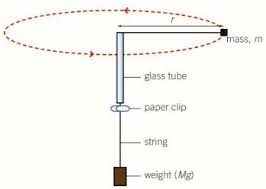
Describe an experiment that can be performed to investigate circular motion?

Include a diagram

A Whirling Bung

• As the bung is swung in a horizontal circle, the suspended weight remains stationary as long as the force it provides (Mg) is equal to the centripetal force required to make the bung travel in a circular path

Explain why velodromes have banked surfaces?

Include a diagram to show the forces acting on the bike

• They are banked so track cyclists can travel at higher speeds

• On a banked part of the track, a horizontal component of the normal contact force, together with the frictional forces of the tyres provide a centripetal force required to follow the circular path at such high speeds

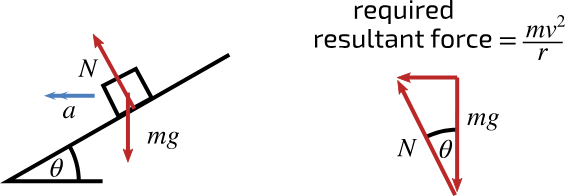
Write an expression for the horizontal component of the normal contact force that acts towards the centre of the circle, and the vertical component that balances gravity?

• Horizontal Component (Provides Centripetal Force)

  Nsinθ = mv²/r

• Vertical Component (Balances gravity)

  Ncosθ = mg

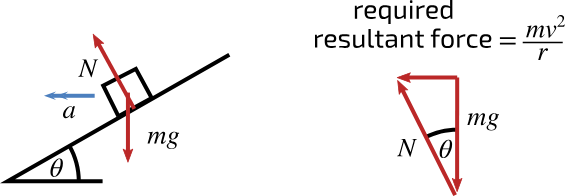
How would you calculate the banking angle of the surface, if you have the horizontal and vertical component of the normal contact force?

• tanθ = horizontal component / vertical component

• Nsinθ / Ncosθ = mv²/r / mg

• → tanθ=v² / rg

Draw a diagram of the forces and their directions in a Vertical Circular Motion?

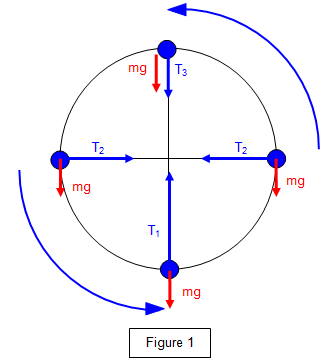
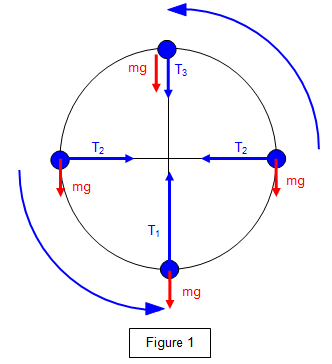
Write an Expression for each net force at each location?

• At the Top → T(3) = mv²/r - mg

• At the middle → T(2) = mv²/r

• At the Bottom → T(1)= mv²/r + mg

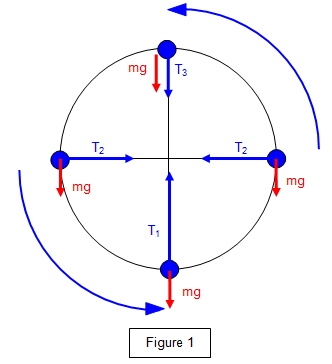
When would someone feel weightless during a vertical circular motion and why?

At the top of the circle,

The centripetal force is equal in magnitude and opposite in direction to the force of gravitational attraction, resulting in weightlessness.

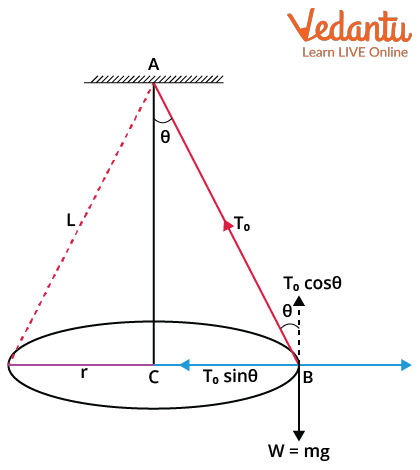
Draw a diagram of a conical pendulum and show the forces that are acting on the pendulum bob?

• Horizontal Component → Mv²/r = Tsinθ

• Vertical Component→ mg=Tcosθ

Vertical component of the tension must be equal to the weight of the plumb bob because there is no acceleration in vertical direction

→F(T)cosθ=mg

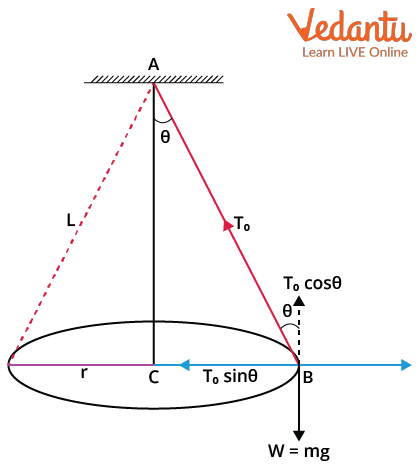
Derive an expression relating the angle of the pendulum to its speed and its radius?

• F=mv²/r

• r=Sinθ X L

• √v² = Fr/m