Cap#6: Matrices
Studied by 0 people
Knowt Play
Learn
Practice Test
Spaced Repetition
Match
Flashcards1/34
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
35 Terms
¿Qué es la traza?
Se trata de la suma de los elementos de la diagonal principal.
Matriz triangular superior
Debajo de la diagonal hay ceros.
Matriz triangular inferior
Arriba de la diagonal hay ceros.
Matriz diagonal
Ceros arriba y abajo de la diagonal.
Matriz escalar
Matriz diagonal pero su número se repite.
Matriz identidad
Matriz diagonal pero solo hay 1’s.
Multiplicación entre matrices
Solo pueden multiplicarse si la columna de A es igual a la fila de B.
Potenciación de matrices
Solo con matrices cuadradas.
Se produce una multiplicación entre la misma matriz.
Transposición de matrices
Se intercambian sus filas por columnas y viceversa.
\left(A^{T}\right)^{T}
A
\left(A+B\right)^{T}
A^{T}+B^{T}
\left(kA\right)^{T}
kA^{T}
\left(AB\right)^{T}
A^{T}B^{T}
Fórmula de Determinante de Matriz 2×2
\det\left(A\right)=\left|A\right|=ad-bc
Sea la matriz Anxn:
\det\left(A\right)=0
No tiene inversa
No invertible
Singular
Sea la matriz Anxn:
\det\left(A\right)\neq0
Tiene inversa
Invertible
Regular
Matriz inversa 2×2
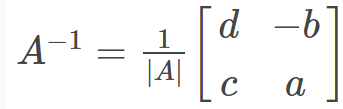
A\cdot A^{-1}
I
Determinante de Matriz 3×3
Escoge una fila o columna, pref. la 1er fila y colócale la matriz signo.
Encuentra determinante de 2×2 tapando la columna.
Matriz inversa 3×3
De cada elemento seleccionado, se tapa su fila y columna y calcula su determinante 2×2.
Se le coloca los signos de acuerdo a la matriz signo. “Matriz de Cofactores”
Sacar inversa mediante:
A^{-1}=\frac{1}{\det\left(A\right)}\cdot\left(\overgroup{A}\right)^{T}
Determinante de una matriz ______ _______ e _____, ______, ______, ______ es el producto de los elementos de la diagonal principal.
Triangular superior
Inferior
Diagonal
Escalar
Identidad
\det\left(A^{T}\right)
\det\left(A\right)
\det\left(A^{-1}\right)
\frac{1}{\det\left(A\right)}
\det\left(kA\right)
k^{n}\cdot\det\left(A\right)
\det\left(AB\right)
\det\left(A\right)\det\left(B\right)
Si se intercambian 2 filas o 2 columnas de una matriz,…
El determinante cambia de signo.
Si se multiplica a toda una fila o toda una columna por un número real,…
El determinante se multiplica por dicho número.
Si se multiplica a toda una fila o columna por un número, pero se suma ese resultado a otra fila o columna,…
El determinante no cambia.
Matriz Simétrica
A=A^{T}
Matriz Antisimétrica
A=-A^{T}
Matriz Involutiva
A^2=I
Matriz Idempotente
A^2=A
Matriz Periódica
A^{P}=A
Matriz Nilpotente
A^{n}=0
Matriz Ortogonal
A^{T}=A^{-1}