Biostatistics exam 3 - one sample t-test

t distribution equation

t = the t - value

Ybar = mean

SEybar = standard error

s = standard deviation

n = sample size

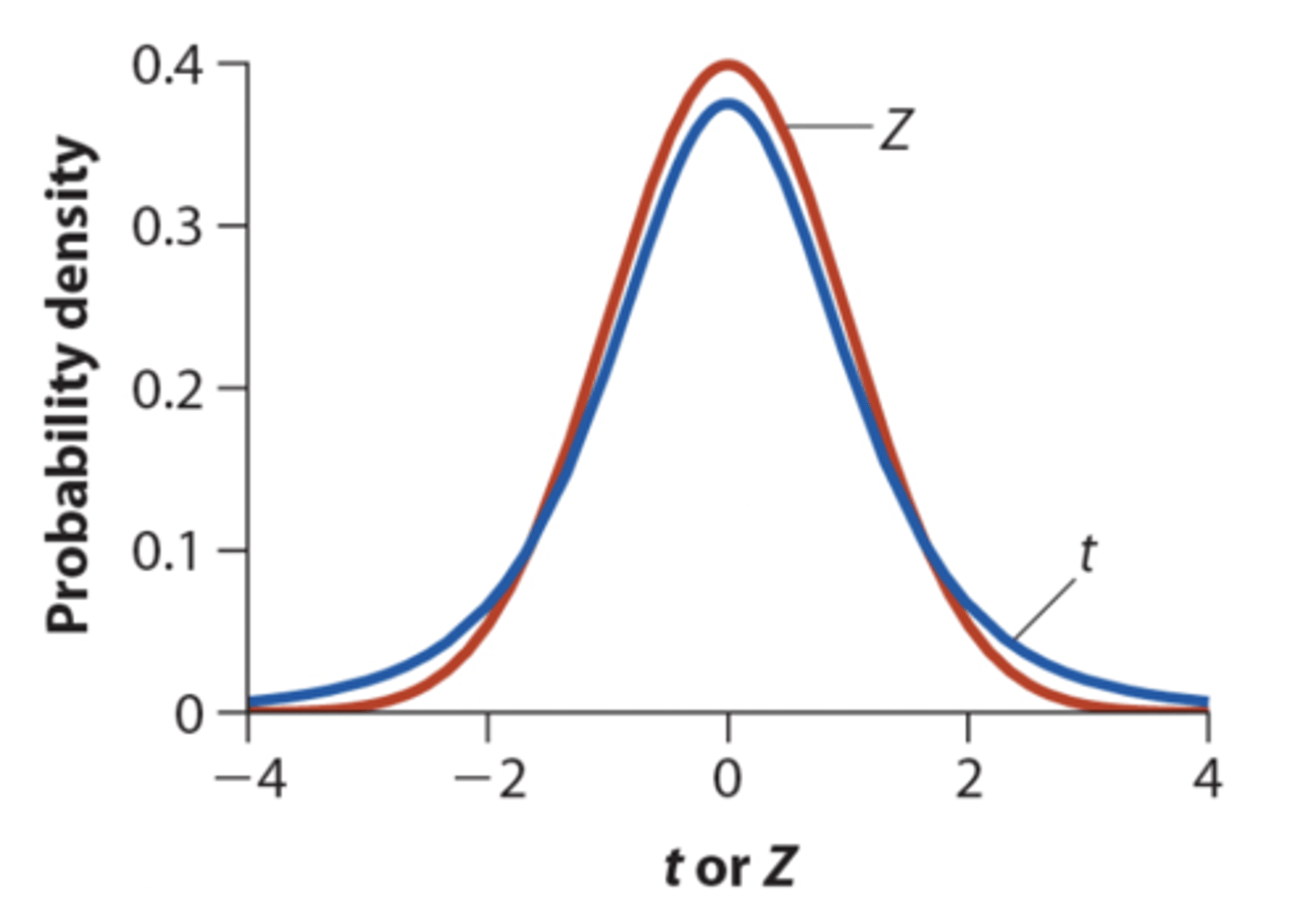
t vs Z distribution curve

• Similar to a standard normal distribution but with fatter tails

• as a sample size increases the t distribution becomes more like the standard normal distribution

• the curve of the t distribution is pushed down and the tails out

• for t distribution the data has to be more extreme to be in the area above the critical value to reject the null hypothesis

• the critical value for significance is moved higher on a t distribution

when can you use a t distribution to accurately calculate a confidence interval?

when the mean of a population has a normal distribution

95% confidence interval for the population mean using the t-distribution (Equation)

t₀.₀₅(₂),df → this indicates that it is a two-tailed test because on one side of the distribution curve: t₀.₀₂₅(1)

One sample t-test

compares the mean of a random sample from a normal population with the population mean proposed in a null hypothesis

One sample t-test hypotheses

H₀: the true mean equals µ₀ (null mean)

Ha: the true mean does not equal µ₀

The test statistic for a one sample t-test

t-value: measures discrepancy between observed and expected

• Note: if the observed mean is close to µ₀ then the numerator will be closer to zero (think about the t -curve)

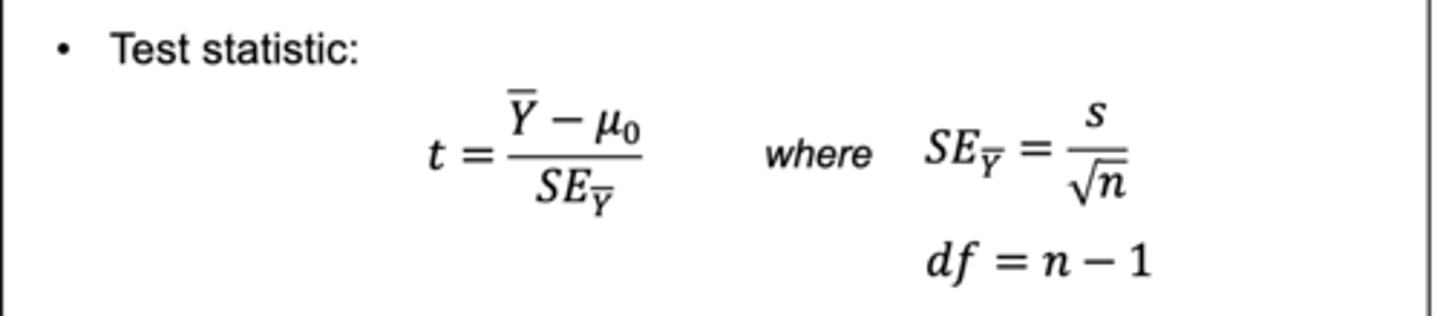
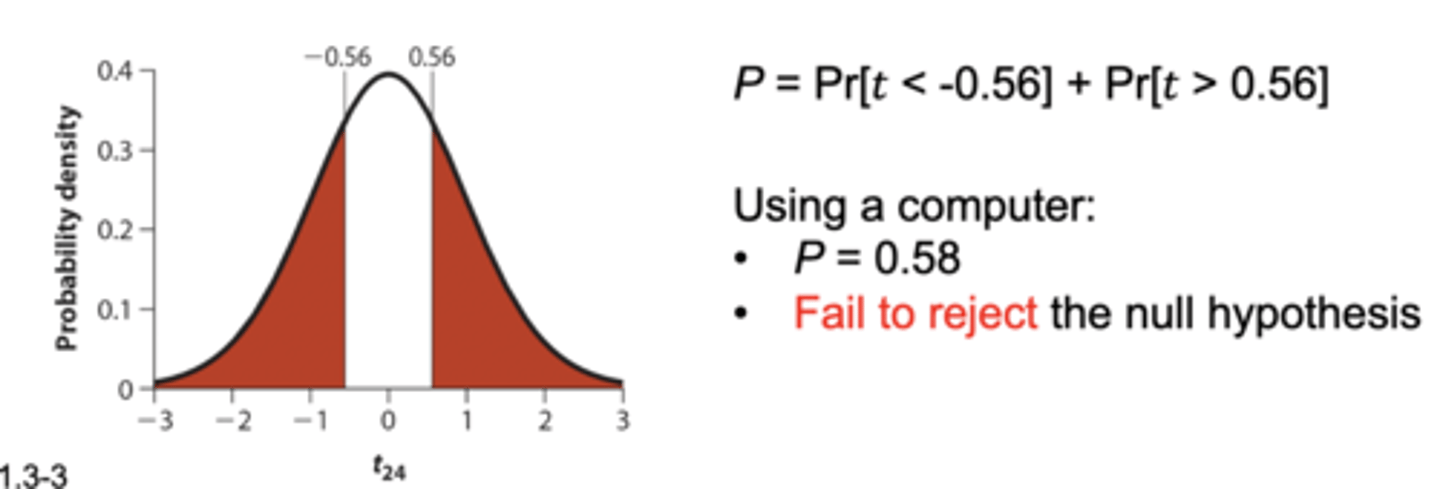
how to compute the p-value for a one sample t-test (using a computer)

Compute p-value: the probability of this test statistic or more extreme given the null hypothesis is true

• for this example, the t-stat was t₂₄=-0.56

• Pr = the area under the Curve greater than the t statistic and the area under the Curve on the opposite side of the Curve (see the red shading in pic)

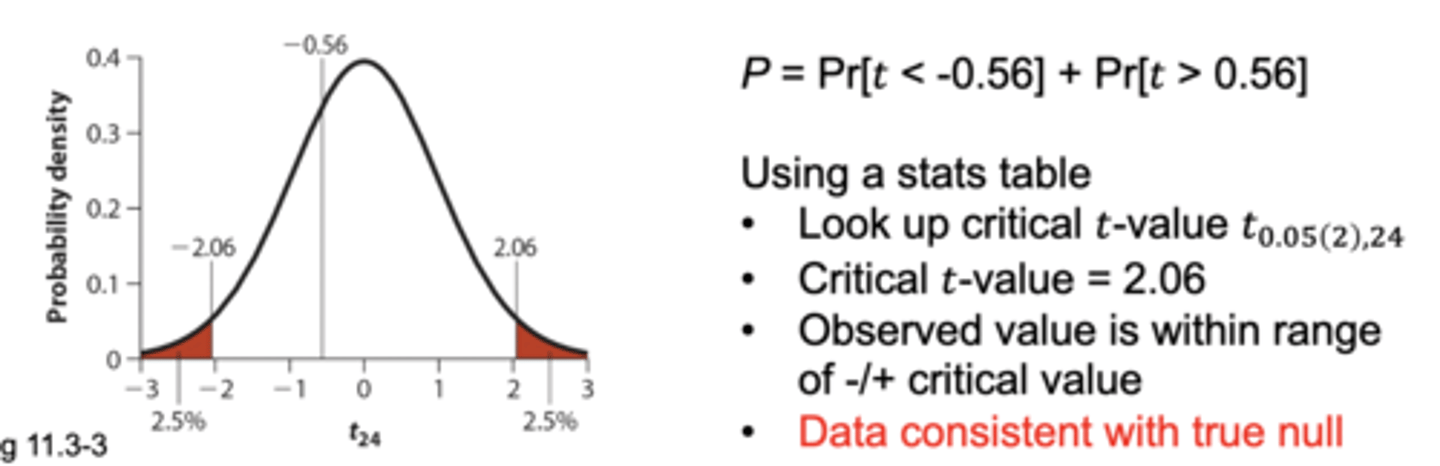
Using a stats table to interpret a t-statistic

• look up critical t-value t₀.₀₅(₂),df

• critical T value equals 2.06 (in this example)

• observed value is within range of +/- critical value (in this example)

• data is consistent with true null (in this example)

using a 95% confidence interval to interpret a t-statistic (one sample)

• the 95% confidence interval tells us how much uncertainty is in our estimate of µ

• in the pic 2.06 is the critical value

how does increasing sample size influence a one sample t-test?

• increasing sample size reduces standard error of the mean (uncertainty of estimate of mean)

• the t-statistic will be larger because sample size is smaller

• the 95% CI will be narrower

• larger sample sizes increase probability of rejecting a false null hypothesis (increase in power)

• (in this example) if this null is really false, then the sample of 25 failed to detect a false null (Type II error)

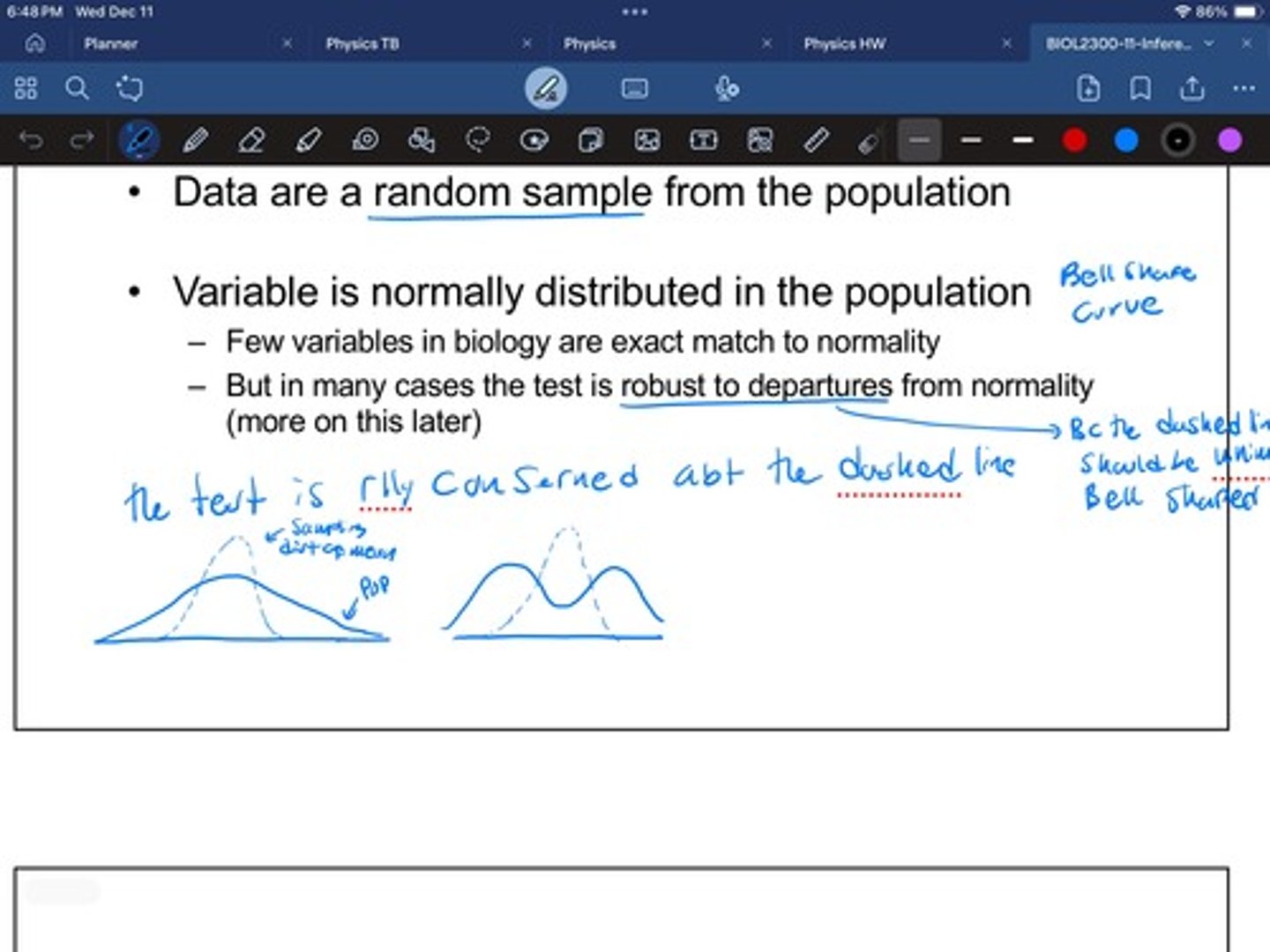
Assumptions of a one sample t-test

1. random sample

2. Variable is normally distributed in the population

- few variables in biology are exact matches to normality

- but in many cases the test is robust to departures from normality

estimating other statistics with a one sample t-test

• there is an emphasis on estimating the mean of a normal population

• how about other statistics

- spread of the sample distribution (standard deviation or variance)

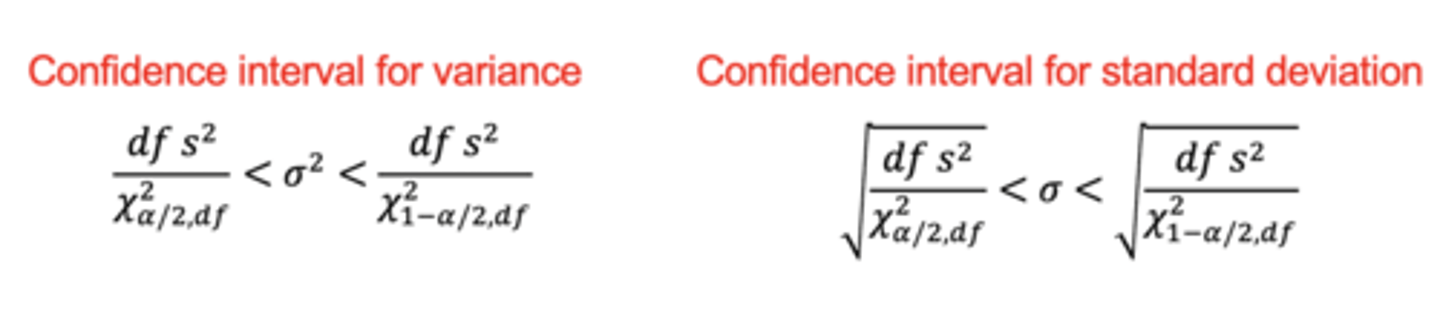
Confidence limits for variance is based on the _________ distribution

X² distribution

Confidence interval for variance equation versus for standard deviation

The variance equation is squared

The standard deviation is the square root of variance

Assumptions of calculation for confidence intervals for variance

1. Random sample from the population

2. Variable must have normal distribution

- formulas are NOT robust to departures from normality