HOC 1 econometrie vs beschrijvende statistiek

Econometrie

is een discipline binnen de economische wetenschap die als doel heeft een kwantitatieve beschrijving te geven van de relaties tussen economsisceh variabelen, en overstijgt dus het descriptieve karaketer van samenvattende statistieken

we toetsen theoretische hypotheses en maken voorspellingen

samenvoeging van economische theorie, wiskunde en statistiek

inferentiele statistiek

statistische methoden die gebruik maken van de beschikbare data (steekproef) om zo een uitspraak te maken omtrent het (onzichtbare) onderliggende DGP → data generatie proces

→ het model dat wij opschrijven, wij gaan ervan uit dat dit de manier is waarop de data die wij observeren werkelijk ontstaat

→ op basis van deze parameetrs is deze data ontstaan

→ zo kan je voorspellen

inferentiële statistiek : eigenschappen van het proces

validatie van gemaakt assumpties via hypothesetoetsen

schatten van parameters en kwantificeren van onzekerheid omtrent deze schatting

verschil inferentiele en beschrijvende statistiek

beschrijvende statistiiek gebruikt numerieke en grafische methodes om data te beschrijven en samen te vatten

→ uitspraken maken over de populatieparameters

→ statische beschrijving van de groep/ steekproef en hopelijk zegt het iets over de populatie

assumptie van homogenitiet

algemeen is een zekere homogeniteit in de steekproef vereist zodat we geen appelen en peren vergelijken

we willen als minimum reallisaties uit verdelingen met hetzelfde gemiddelde

(→ iedereen deelt dezelfde kansvariabele )

soorten data : cross-sectionele data

afhankelijkheid tussen andere entiteiten over dezelfde periode

vb oinflatie in belgie, nederland, frankrijk in 2019

soorten data : tijdsreeks data

afhankelijkheid van dezlefde entiteit over verschillende periodes

vb inflatie in belgie over de jaren 90

soorten data : panel (longitudinale) data

afhankelijkheid tussen andere entiteiten en over verschillende periodes

vb inflatie in belgie, nederland, frankleijk pver de jaren 90

Datageneratieprpces (DGP)

we zijn geïnteresseerd in het stochastische proces dat de kansvariabele Y genereert

we specifieren voor dit DGP een model, met (onbekende) parameters die we dienen te schatten

in dit model hangt de kansvariabele Y af van :

• andere manifestaties van dezelfde kansvariabele Y (vb punten van vorige jaren)

• andere (voorspellende of verklarende) kansvariabelen X (vb aantal uren dat je naar d eles bent gekomen)

E[Y]

is de onconditionele verwachte waarde van een kansvariabele Y

E[Y!X] (met ! = streep)

is de verwachte waarde van een kansvariabele Y conditioneel op een kansvariabele X

indien X en Y stochastisch afhankelijk zijn : (relatie conditionele en onconditionele verwachte waarde)

dan hebben we dat E[Y] ≠ E[Y!X]

omwille van de afhankelijkheid kunnen we namelijk een betere voorspellling van Y doen, als X gekend is

wat veronderstellen we in econometrie omtrent de observaties van Y

we veronderstellen dat de observaties van een kansvariabele Y het resultaat zijn van een onderliggend datageneratie proces (DGP)

we specifieren een model voor dit DGP aan de hand van een functionele vorm dat de afhankelijke variabele Y en de onafhankelijke variabele X verbindt

deze functionele vorm bevat onbekende parameters die we dienen te schatten

deterministische relatie (tussen afhankelijke en onafhankelijk variabele)

Y = h(X) waar we de reeelwaardige functie h(.) de functionele vorm noemen

er zit geen fout in, er staat dat je exact Y kan berekenen → komt eigenlijk niet voor

→ er zit variatie

stochastisch relatie tussen afhankelijke en onafhankelijke variabele

Y = h(X) + e

met E[x!X] = 0 en Var [e!X] > 0 (assumpties)

de functie h(.) bevat onbekende parameters die we dienen te schatten

je neemt expliciet in jouw model dat er fouten zullen zijn

we moeten uiteindelijk tot een lineaire regressie komen

functie h is lineair

Y = a + bX +e

i.i.d

een sterke assumptie op het datageneratie proces is dat een variabele onafhankelijk en gelijk verdeeld (independently and identically distributed) is

we stellen hier dat de kansvariabele Y iid is met een onbekende parameter : een verwachte waarde mu en een variantie o²

we dienen deze parameters te schatten

soms maken we de nog sterkere assumptie van iis in sombinatie met normaal verdeeld

iedereen heeft dezelfde mu en variantie → dezelfde distributie

en de studneten hebben geen invloed op elkaar

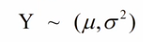
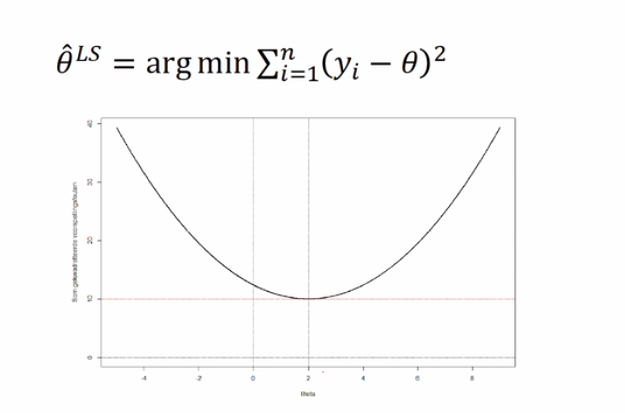
kleinste kwadratenschatting (om theta = verwachte waarde van Y te schatten)

theta zo kiezen dat het gekwadrateerde verschil tussen de geobserveerde data en de locatieparameter minimaal is

eerste en tweede orde conditie minimum (LSE)

uit de eerste orde conditie volgt dat de kleinste kwadratenschatter het steekproefgemiddelde is

de tweede afgeleide is steeds positief en geeft dus aanleiding tot een minimum

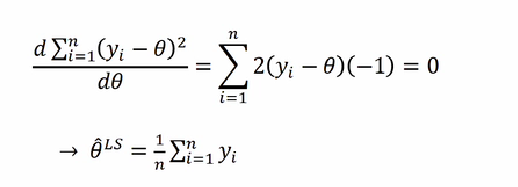
hoe kan het steekproefgemiddelde worden gezien onder sterke assumpties

als de beste locatie schatter in termen van keinste gekwadrateerde voorspellingsfouten → iid

maar verwachte waarde, variantie en verdeling van de schater gaan afhangen van de gemaakte assumpties

interpretatie van theta ^ descriptief en inferentieel

descriptief : theta ^is het gemiddelde van de steekproef

inferentieel : theta ^zegt iets over de verwachte waarde van het onderliggende datageneratieproces

→ om deze inferentie te kunnen doen, moete we extra assumpties maken over het DGP die y1,,,n heeft gegenereerd

berekening van de variantie (onder assumpties DGP : gelijke verwachte waarde en variante + onafhankelijkheid (iid) )

hoe precies is de schatter → variantie rond de schatter

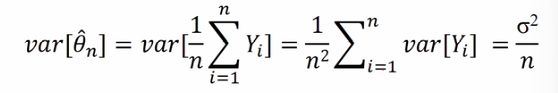
extra assumptie DGP

iid normaal verdeeld

onder de assumptie van onafhankelijke trekkingen uit dezelfde normale verdeling

is het steekproefgemiddelde ook normaal verdeeld

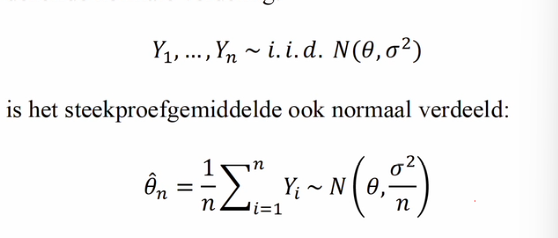
theta ^

is een puntschatting van de populatieparameter theta

door steekproefvariabiliteit is het zo dat als de steekproef niet oneindig groot is dat that ^ =! theta

vandaar het belang om naast een punstchatting van theta ook een interval schatting te hebben van theta