Physics - Alternating Current

Alternating Current  

It is one for which the magnitude and direction of current changes continuously with time.

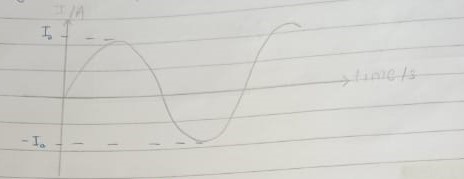
Time Period (T)

Time period of an AC cycle, representing the duration of one complete cycle of the waveform.

Frequency (f)

f = 1/T, where f is the frequency and T is the time period

Angular Frequency, w 

• Rate of change of current or voltage

• w = (2π)/T , where T is the time period

• w = 2πf, where f is the frequency

Peak Current

The Amplitude of the graph

I = I₀ x sin wt, where I₀ is the peak current, w is 2πf or (2π)/T (f is the frequency and T is the time period), t is the time period and I is the current

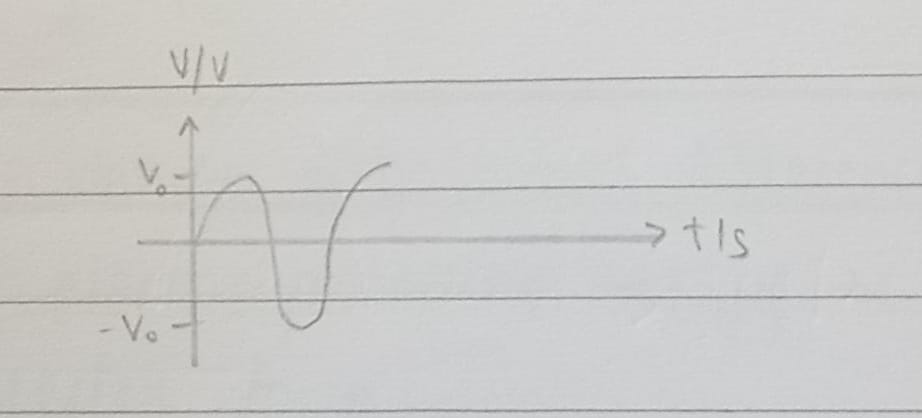
Peak Voltage 

V = V₀ x sin wt, where V is the voltage, V₀ is the peak voltage, w is 2πf or (2π)/T (f is the frequency and T is the time period), and t is the time period 

Power

• P = (I₀)² x R x sin² wt, where P is power, I₀ is peak current, R is resistance, w is 2πf or (2π)/T (f is the frequency and T is the time period), and t is the time period 

• P = IV , where P is power, I is current, and V is voltage

• P = I₀V₀, where P is power, I₀ is peak current and V₀ is peak voltage

• P = I²R, where P is power, I is current, and R is resistance

Maximum Power 

Pₘₐₓ = (I₀)²R, Pₘₐₓ is maximum power, I₀ is peak current, and R is resistance

Minimum Power

Pₘᵢₙ = 0, where Pₘᵢₙ is minimum power

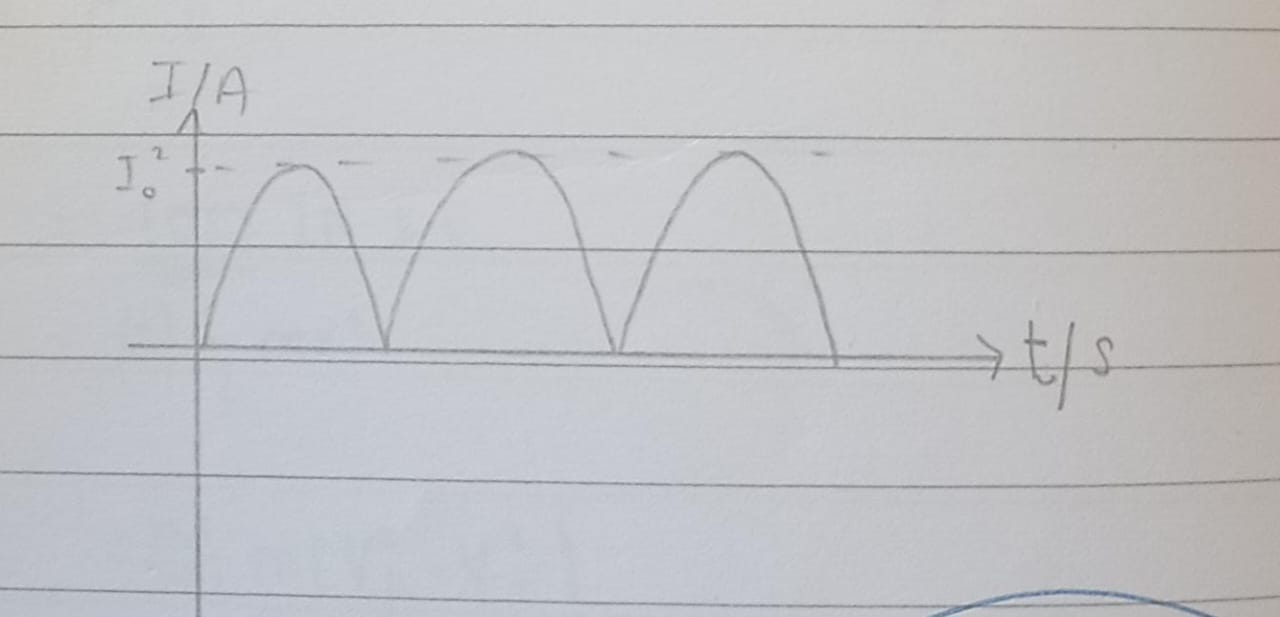
Mean Power

• P_mean = ½ Pₘₐₓ, where Pₘₐₓ is the maxiumum power, and P_mean is the mean power

• P_mean = ½ x (I₀ )² x R, where I₀ is peak current, R is resistance, and P_mean is the mean power

• P_mean = ½ x I₀ x V₀, where P_mean is the mean power, I₀ is the peak current, and V₀ is the peak voltage

• P_mean = V_rms x I_rms, where P_mean is the mean power, V_rms is the root mean squared voltage, and I_rms is the root mean squared current

Iₘₛ (Mean Squared)

Iₘₛ = ( ½ x (I₀)²), where I_ms is the mean current squared and I₀ is the peak current 

I_rms (Root Mean Squared)

• The value of the direct current corresponding to an alternating one that gives the same mean power output as an alternating current would.

• I_rms = I_o x √(2), where I₀ is the peak current

V_rms (Root Mean Squared)

• The value of the direct voltage corresponding  to an alternating one that gives the same mean power as an alternating voltage would

• V_rms = V₀ x √(2), where V₀ is the peak voltage

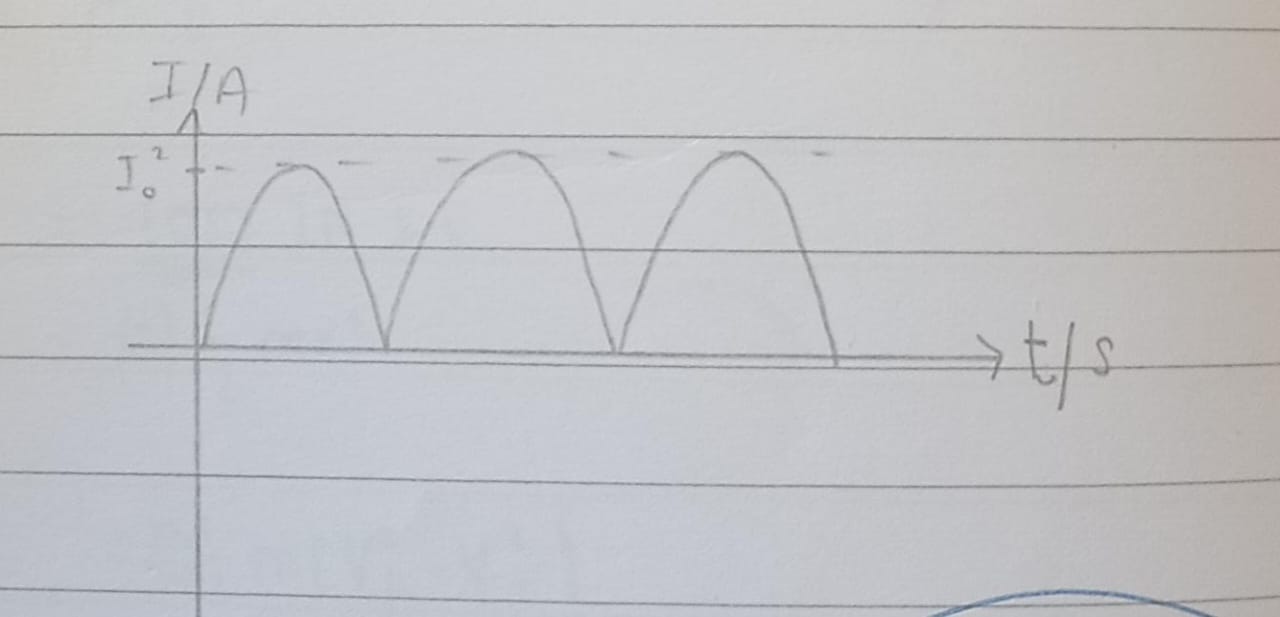
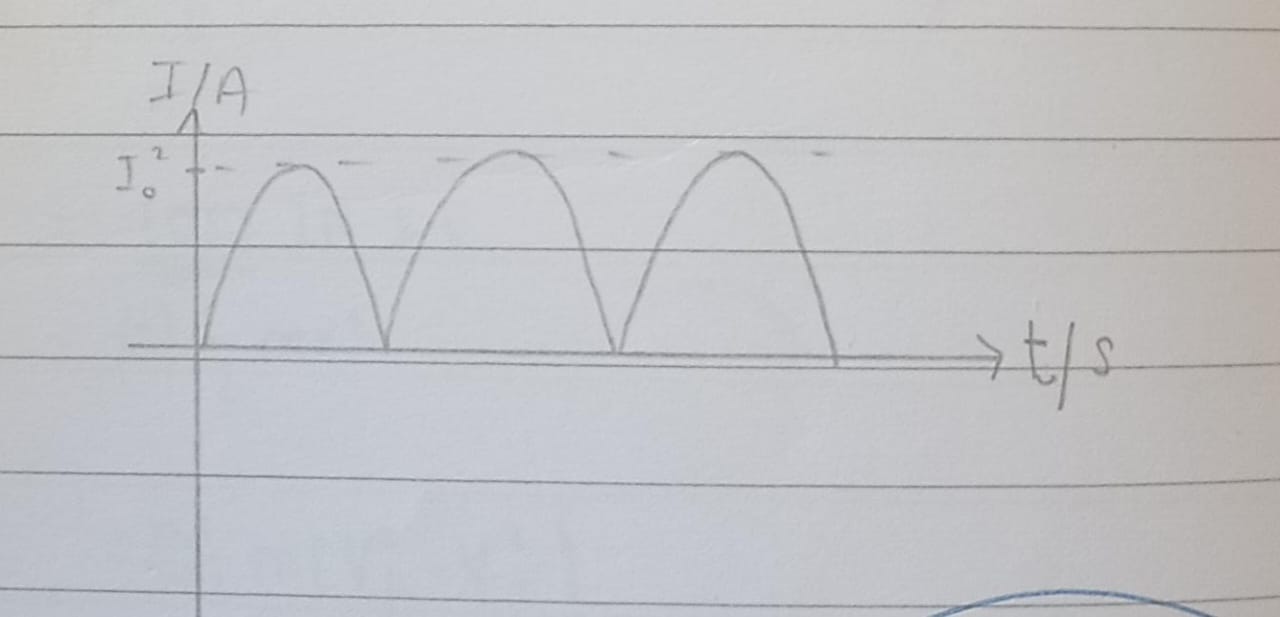
Half-Wave Rectification graph

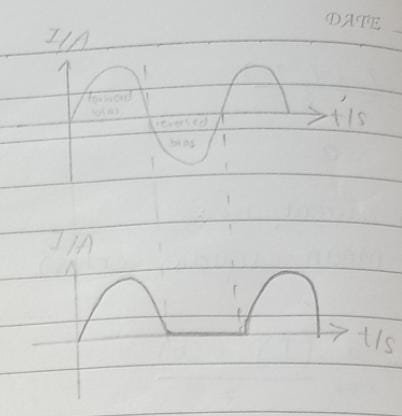
Full-Wave rectification graph

Use of single diode for a half-wave rectification of an alternating current

A single diode converts only one half-cycle of AC into pulsating DC. It acts as a one-way valve, letting current flow during one half-cycle and blocking it during the other. This 'chops off' half of the AC waveform, creating a pulsed DC output

Use of the bridge rectifier (four diodes) for the full-wave rectification of an alternating current

A bridge rectifier uses four diodes to convert a full cycle of AC into pulsating DC. It achieves this by guiding the current to always flow in the same direction through the load, regardless of the AC input's polarity. This method utilizes both halves of the AC waveform, making it more efficient than half-wave rectification.

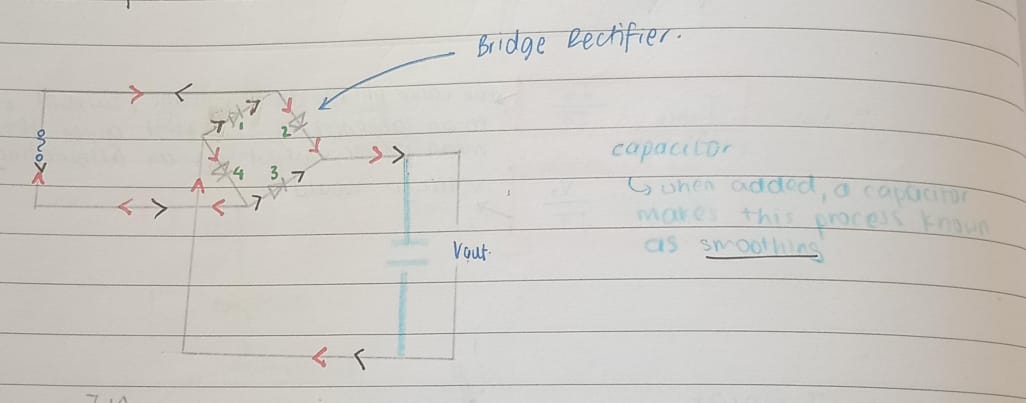
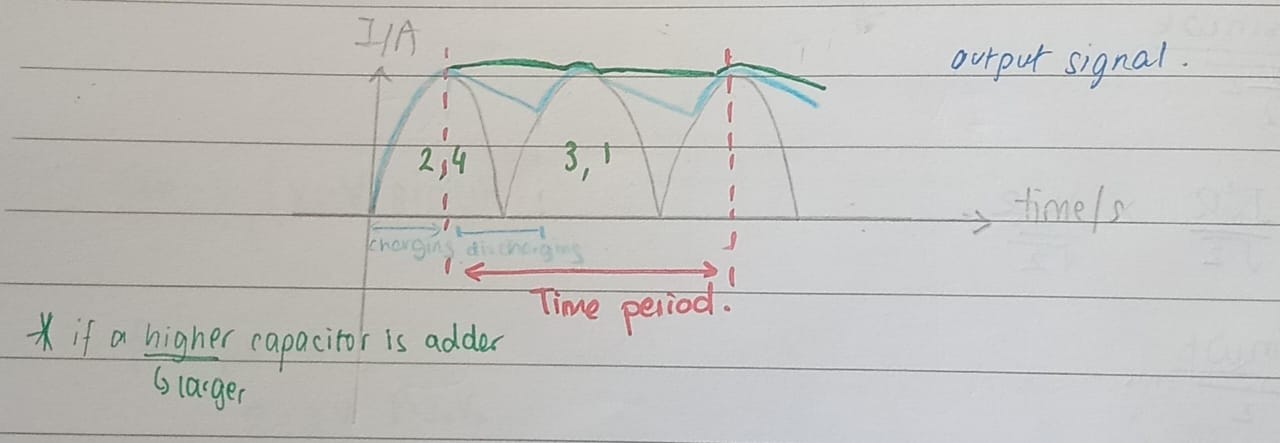
Smoothing

To decrease the drop in the output voltage, a capacitor is attach in parallel to the V_out. Adding a capacitor increases the mean output voltage and hence also increases the mean output voltage.