Stat Econ Module 2

Two numerical ways of describing data

1. Measures of Location

2. Measures of Dispersion

Measures of Location (Central Tendency)

Pinpoint the center of a set of values.

Considering only measures of __________ can lead to erroneous conclusions; dispersion provides crucial additional context.

Measures of Dispersion (Variation/Spread)

Describe the spread or variability of the data.

Population

all the possible values or observations

Sample

a subset drawn from a population

Population Mean

The sum of all values divided by the number of values.

Population Mean Formula

μ = (ΣXᵢ) / N

where…

μ = __________

(ΣXᵢ) = sum of all X values in the population

N = number of values in the population

Parameter

any measurable characteristic of a population

ex: the mean of a population is an example of this

Parameter vs. Statistic

Parameter is any measurable characteristic of a population.

Statistic is any measurable characteristic of a sample.

Sample Mean Formula

x̄ = (ΣXᵢ) / n

where…

x̄ = ________

(ΣXᵢ) = sum of all x values in the sample

n = number of values in the sample

Statistic

Measure based on sample data

ex: mean of a sample

Properties of the Arithmetic Mean

• A mean exists for every set of interval or ratio-level data.

• Includes all values in computing the mean.

• A mean is unique for any given data set.

• The sum of deviations from the mean is always zero: Σ(X- x̄) = 0

Summation Properties

Weakness of the Mean

Unduly affected by unusually large or small values (outliers), making it potentially unrepresentative.

Weighted Mean

Used when some values are more important than others. Each value is multiplied by its corresponding weight, summed, and then divided by the sum of the weights.

Ex: calculating for grades (where some are weighted more than others)

Weighted Mean Formula

(w₁x₁ + w₂x₂ + ... + wₙxₙ) / (w₁ + w₂ + ... + wₙ) = (Σwᵢxᵢ) / (Σwᵢ)

where…

the weight (w₁) of x₁ times x₁ plus the the weight (w₂) of x₂ times x₂… divided by the sum of the weights

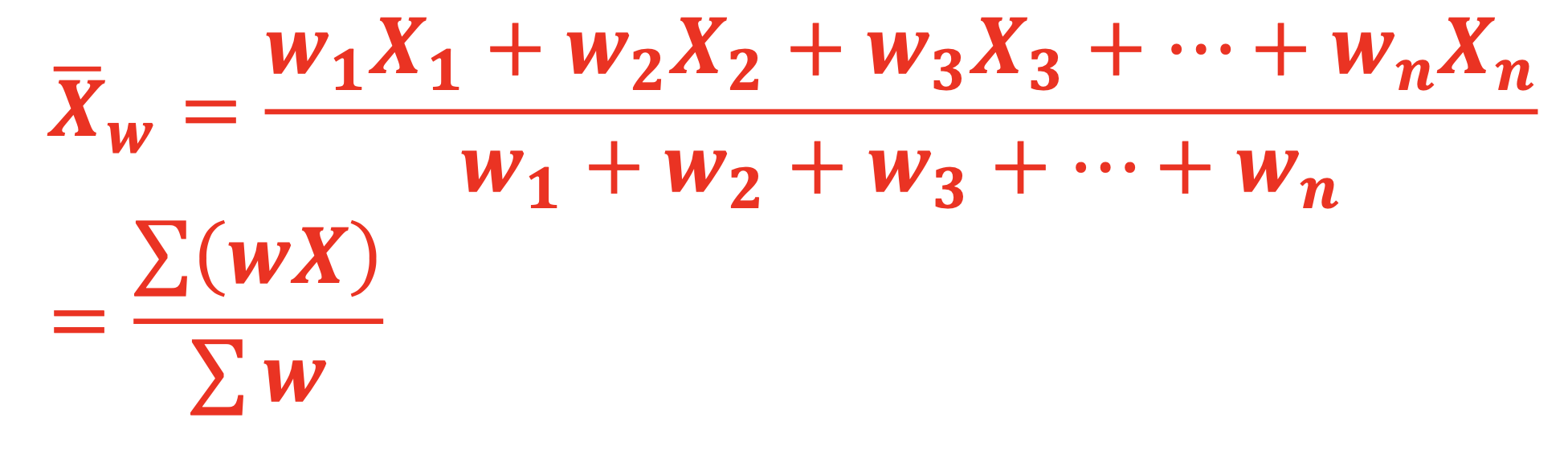
Median

The midpoint of the values after they have been ordered from smallest to largest or largest to smallest.

Odd number of observations: The middle observation.

Even number of observations: The mean of the two middle observations. (May not be one of the original values).

Advantage: Unaffected by outliers

Mode

The value that appears most frequently in a data set.

Disadvantages

• May not exist (no value appears more than once).

• May have multiple modes (bimodal, multimodal).

• Less frequently used than mean or median.

Mean = Median = Mode

for a symmetric mound-shape distribution

Skewed distribution

not symmetrical

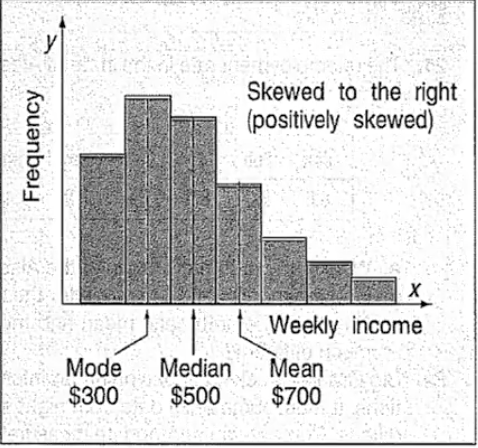
positively skewed distribution

a data distribution where most values are concentrated on the left side of the graph; skewed to the right (looks like a p)

the arithmetic mean is the largest of the three measures because the mean is influenced more than the median/mode by a few extremely high values

the median is the next largest measure in a ___________

mode is the smallest

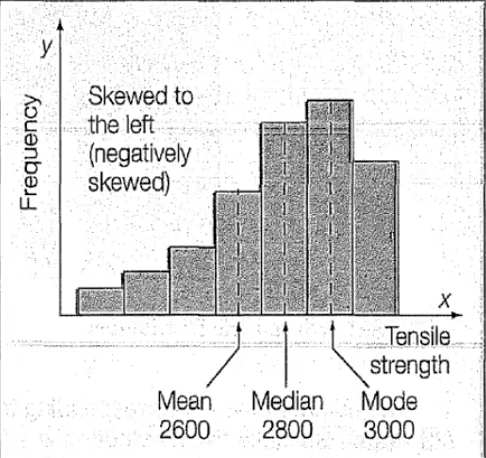
negatively skewed distribution

a data distribution where most values are concentrated on the right side of the graph (skewed to the left)

mean is the lowest of the three measures, influenced by a few extremely low observations

median is greater than mean

mode is the largest of the three

Mode is usually used for…

nominal-level data

Median is usually used for…

ordinal-level data

Mean is usually used for…

ratio-level data

Geometric Mean

useful for finding the average of percentages, ratios, indexes, or growth rates

ex: GDP which compound or build on each other

Geometric Mean Formula 1

n is the total number of terms (X) that are being multiplied

GM ≤ Arithmetic Mean

All data values must be positive

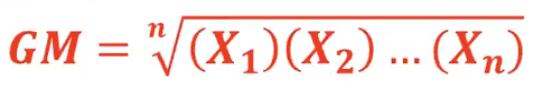
Geometric Mean vs. Arithmetic Mean

_________ uses addition and division to find the average of a set of numbers, while _________ uses multiplication and roots to find the average, particularly for growth rates or ratios.

The AM is suitable for additive data, while the GM is better for multiplicative relationships, such as investment returns or population growth, and requires positive numbers.

Geometric Mean Formula 2

to find an average percent increase over a period of time

ex: financial economics