Parabola Equations and Properties (Conic Sections)

23 question-and-answer flashcards covering parabola definitions, focus/directrix properties, parameter p, vertical and horizontal conic forms, orientation rules, function test, derivation, and worked examples.

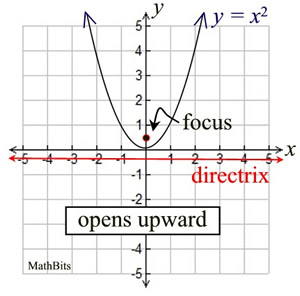
What is the geometric definition of a parabola?

The set (locus) of all points that are equidistant from a fixed point called the focus and a fixed line called the directrix.

For any point on a parabola, what two equal distances define its position?

The perpendicular distance to the directrix equals the distance to the focus.

Where is the focus located relative to a parabola?

On the axis of symmetry, inside the parabola, at a distance p from the vertex.

Where is the directrix located relative to a parabola?

Outside the parabola, perpendicular to the axis of symmetry, at a distance p from the vertex.

What does the parameter p represent in parabola equations?

The distance from the vertex to the focus (and also from the vertex to the directrix).

How is p related to the leading coefficient a in the quadratic y = ax² (vertex at origin)?

p = 1/(4a).

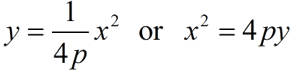
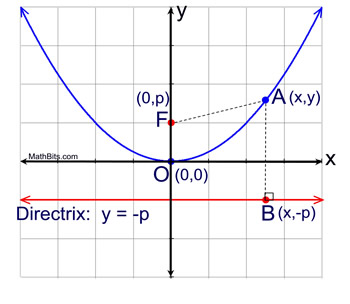
Write the conic form of a vertical parabola (axis parallel to y-axis) with vertex at the origin.

x² = 4py or equivalently y = (1/4p)x².

What are the focus and directrix for x² = 4py?

Focus (0, p); Directrix y = –p.

Write the conic form of a vertical parabola with vertex (h, k).

(x – h)² = 4p(y – k).

For (x – h)² = 4p(y – k), where are the focus and directrix?

Focus (h, k + p); Directrix y = k – p.

Write the conic form of a horizontal (“sideways”) parabola with vertex at the origin.

y² = 4px or equivalently x = (1/4p) y².

What are the focus and directrix for y² = 4px?

Focus (p, 0); Directrix x = –p.

Write the conic form of a horizontal parabola with vertex (h, k).

(y – k)² = 4p(x – h).

For (y – k)² = 4p(x – h), where are the focus and directrix?

Focus (h + p, k); Directrix x = h – p.

How do you determine whether a vertical parabola opens upward or downward?

For x² = 4py, if 4p > 0 (p > 0) it opens upward; if 4p < 0 (p < 0) it opens downward.

How do you determine whether a horizontal parabola opens right or left?

For y² = 4px, if 4p > 0 (p > 0) it opens to the right; if 4p < 0 (p < 0) it opens to the left.

Why are parabolas that open right or left not functions?

They fail the vertical line test because a vertical line can intersect the graph in more than one point.

What equation results from deriving a parabola via the distance formula with vertex at (0,0) and directrix y = –p?

x² = 4py.

Given x² = 16y, what is p, the direction of opening, and the focus?

p = 4 (since 4p = 16), parabola opens upward, focus (0, 4).

Given (x – 3)² = –8(y – 2), what is p, the direction of opening, focus, and directrix?

p = 2 (because 4p = –8 ⇒ p = –2 in sign), opens downward, focus (3, 0), directrix y = 4.

What is the equation of a parabola with vertex at the origin and focus (0, –3)?

x² = –12y (since p = –3 and 4p = –12).

Describe the steps to rewrite x² – 6x + 3y + 18 = 0 in conic form and give its vertex.

Complete the square: (x – 3)² = 3(y + 3); vertex (3, –3).

For (x – 3)² = 3(y + 3) from the previous card, does the parabola open up or down, and why?

Down; 4p = 3 is positive? Wait sign? Actually the coefficient of (y + 3) is positive, so p = 3/4 > 0, but because y term appears as (y + 3) on right side (not left), the coefficient is positive, so opens upward? Correction: Conic form standard is (x – h)² = 4p(y – k). Comparing gives 4p = 3 so p = 3/4, positive, so it opens upward.