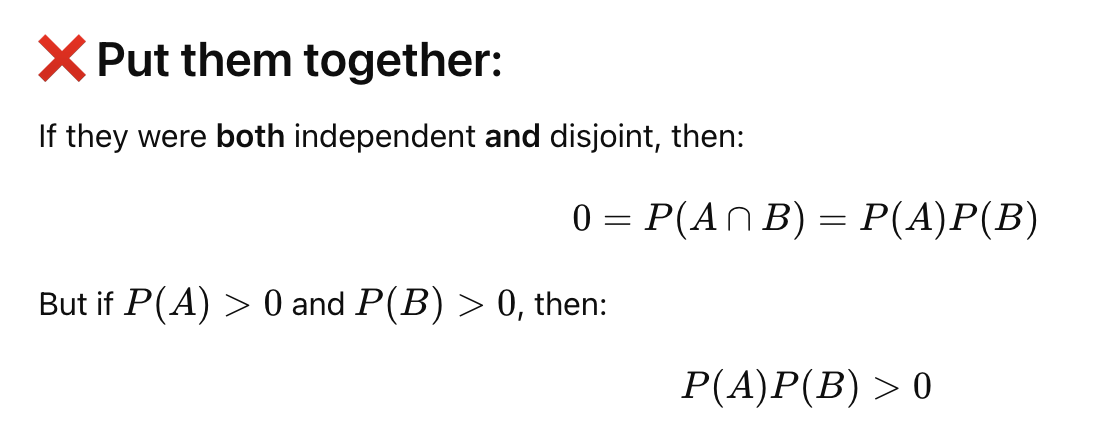AP Stats unit 6

Imitation of chance behavior based on a model that accurately reflects the phenomenon

simulation

List the steps when setting up a simulation:

1. state the ____ or describe a ____

2. state the ____

3. assign ____ to represent ____

4. describe a ___ and what you’ll ____

5. simulate many _____ (use randint)

6. state ur _____

problem, random phenomenon

assumptions

digits, outcomes

trial, measure

repetitions

conclusions

randomness: Short run events are _____, but in _____ we expect reg distribution

unpredictable, long run

probability of random phenomenon is the ____ of times the outcome is _____ to occur in the long run

proportion, expected

law of large numbers

• The more you ____ an event, the more that your experimental probability tends toward ____

• Every future event has ____ influence on overall prob, so u see fewer fluctuations

• Next n events are expected to be ___ to actual prob, so ____ is expected to tend toward actual prob

• does NOT mean that if I flip heads 5 times, tails is more likely next time

• tells you about ____ averages, NOT what the next flip will be (next flip is still independent of past ones)

repeat, actual prob

smaller

close, graph

long-run

a probability model: ____ S (all possible outcomes) with _____ assigned to each event

sample space { }, probabilities

probability models

• infinite, continuous sample space: use a _____

• finite, discrete sample space: ___ or ____

density curve

table, equally likely outcomes

Probability rules

1. probability P(A) of any event A satisfies ___ ≤ P(A) ≤ ___

2. If S is sample space, P(S) = __

3. Complement rule: P(A^c) = ____

0, 1

1

1-P(A)

2 events are _____ if the occurence of one doesn’t affect the probability of the other

independent

sampling ____ replacement: randint

sampling ____ replacement: randIntNoRep

with, without

If A and B are independent P(A ∩ B) = 

P(A) * P(B)

only reason why this works or doesn’t work is that its ind or not ind

If A and B are disjoint/mutually exclusive (can never occur simultaneously), P(A ∪ B) = ______ and P(A∩B) =_____

write these two relationships down!

P(A) + P(B), 0

General addition rule: P(A ∪ B) = ______

P(A) + P(B) - P(A ∩ B)

Strategies for solving probability problems:

Draw a picture of the situation

• overlapping groups and unions/intersections

• categorical counts or percentages in two variables

• multi-stage processes or changing probabilities

• normal distributions, z-scores, percentiles

venn diagram

two-way table

tree diagram

normal curve

Conditional Probability: P(A|B) =

Does P(A|B) always equal P(B|A)

P(A ∩ B) / P(B)

No, if P(A) and P(B) are diff

If events are independent, _____ and _____ Write these two relationships down!

If they’re not equal/independent, they’re ____

P(B|A) = P(B), P(AnB)=P(A)*P(B)

associated

General multiplication rule: P(A∩B)

P(A) * P(B|A)

P(at least one) =

1-P(none)

standard deviation formula ap stats probability

mean formula stats probability

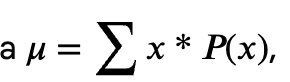
below what probability level would we start questioning whether the claim is true?

0.05

Probability Density Curve

• only requirements: must be positive (always above x axis) and area under it must be __

• does NOT have to be continuous curve, can be piecewise

1

can two events with nonzero probability be both ind and disjoint at same time?

No