Intermediate Macroeconomics Exam 2

How do you find the steady state level of population N* in the Malthus Model

USE THESE TWO KEY EQUATIONS:
N’/N = g(C/N)
C = Y = zf(L,N)

Start with the fact that N’/N = g(C/N), then plug C = zf(L,N) into the equation.

Since N’/N = 1, we can set g(zf(L,N)/N) = 1 and solve for N*

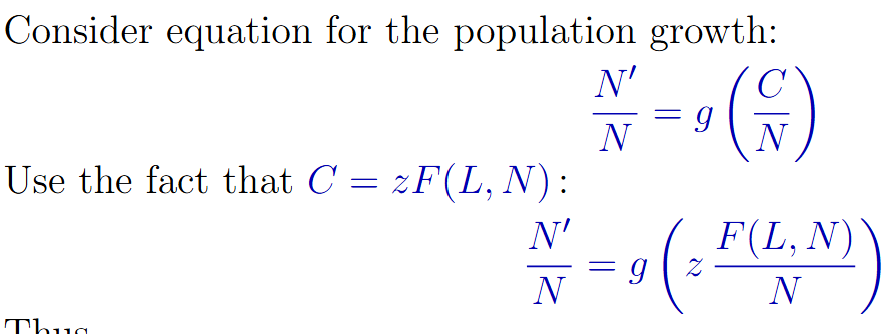
What are the key steady state equations in the malthus model?

c = y = zf(l)
N’/N = g(c)

How do you graph with the Malthus Model

Plot two equations on two different graphs:
find c* from graph 2, then find l* from graph 1 using c*.

How do you find the equation that describes how aggregate capital tomorrow depends on today with the Solow Model

USE THESE THREE KEY EQUATIONS:
K’ = I + (1-d)K
I = S
Y = zF(K,N)

Start with the Aggregate Capital Evolution equation K’ = I + (1-d)K

Then, plug in S for I (likely given)

Finally, plug in the Y that was added from adding S.

From this, we get K’ = szF(K,N) + (1-d)k

How do you find the per worker production function with the Solow Model

USE THESE TWO KEY EQUATIONS
y = Y/N
Y = zF(K,N)

Start with y = Y/N, then plug in Y to get y = zF(K,N)/N

Because of constant returns to scale, we can write this as zF(K/N,N/N)

Since K/N = k and N/N = 1, we get y=zf(k)

How do you rewrite the equation that describes how aggregate capital tomorrow depends on today in per-capita terms with the Solow Model

USE THESE THREE KEY EQUATIONS:
k = K/N
y = Y/N
c = C/N

We use the equation we already found, K’ = szF(K,N) + (1-d)K, and divide by N:

K’/N = szf(k) + (1-d)k

We need to rework K’/N by multiplying it by N’/N’. This should give us something like k’(1+n) = szf(k) + (1-d)k

We can rewrite this as k’ = (szf(k) + (1-d)k)/(1+n)

How do you find steady-state capital per worker k*?

USE THIS KEY EQUATION:
k = k’ = k*

Plug k* into our per-capita aggregate capital equation and solve for k*

What is the growth rate of aggregate variables in the Solow Model steady-state?

All aggregate variables grow at a rate of n. To prove this:

k’ = k => K’/N’ = K/N => K’/K = N’/N => K’/K = 1+n

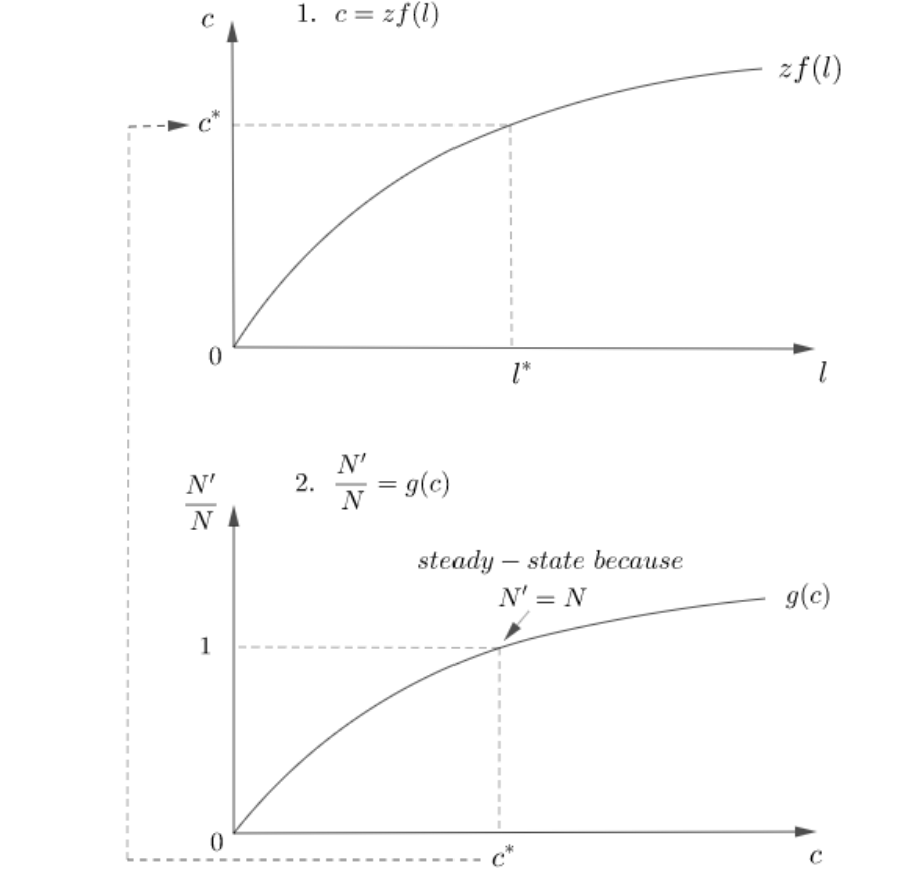
How do you graph with the Solow Model

Make a single graph with the x-axis labeled k and the y-axis unlabeled. Draw the (n+d)k line (straight, increasing) and the szf(k) line. Where they intersect is the steady-state k*.

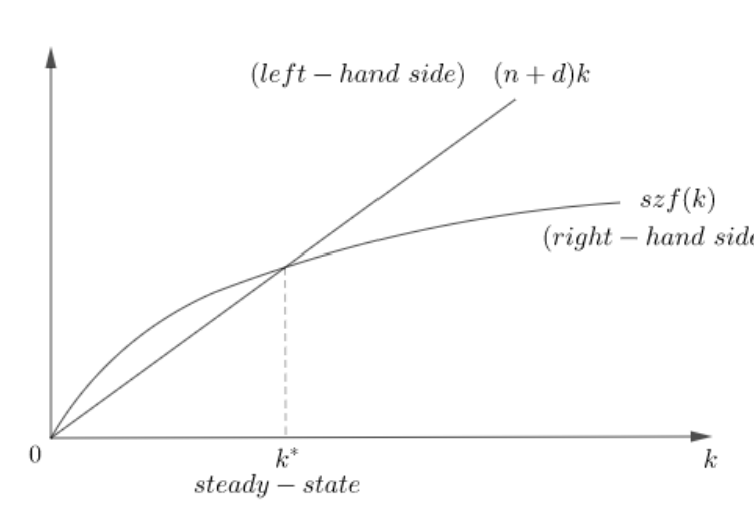
How do you graphically show consumption with the Solow Model

To show consumption, add the output line y=zf(k) above szf(k). The distance between zf(k) and szf(k) at k* is consumption.

What are the assumption equations with the Solow Model

N’/N = (1+n)
Y = zF(K,N)
Y = sY + (1-s)Y
K’ = I + (1-d)K
I = S = sY

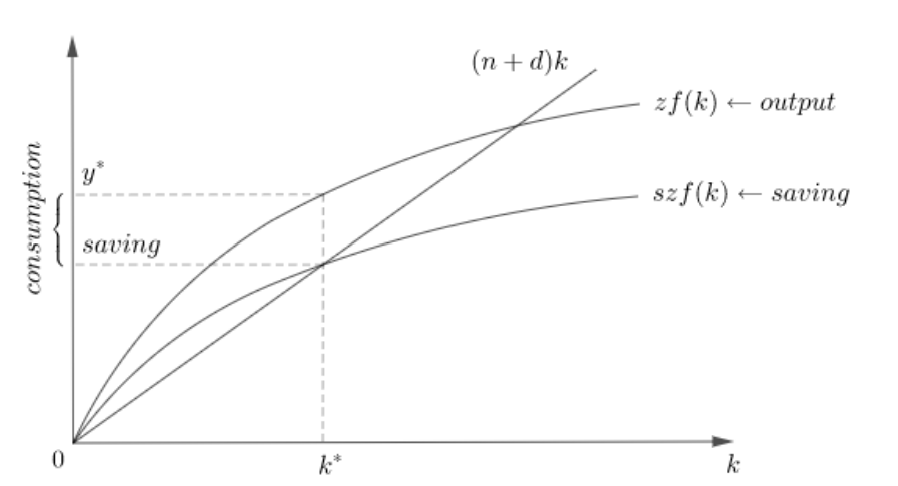
How do you find the golden rule saving state and capital graphically?

The line parallel to (n+d)k and tangent to zf(k) touches zf(k) at the golden rule capital k*_gr. The golden rule saving rate s*gr is the one that yields k*_gr

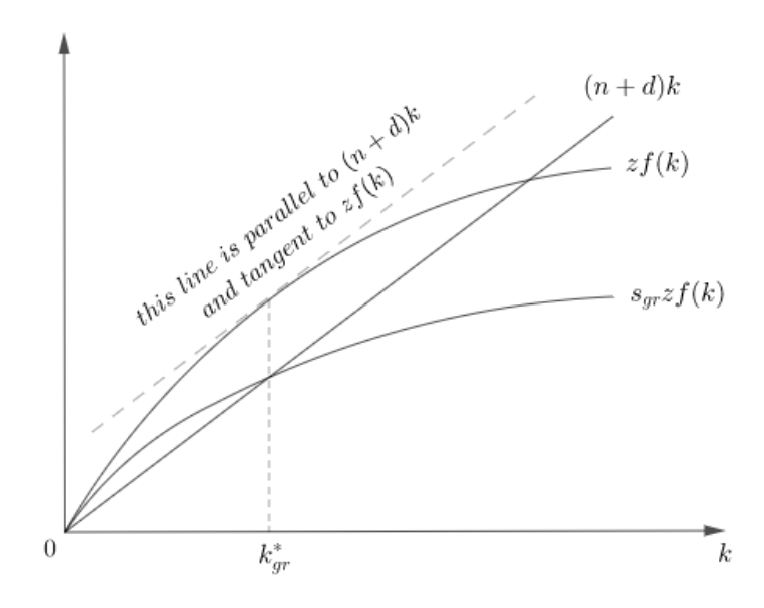
How do you find the golden rule capital analytically?

USE THESE THREE KEY EQUATIONS:
c = (1-s)y
y = zf(k)
szf(k)=(n+d)k (steady state)

Start with the equation c = (1-s)y, then plug in zf(k) for y. This gives you zf(k) - szf(k). Since in the steady state, szf(k)=(n+d)k, we now have:

c = zf(k) - (n+d)k → max k.

In order to maximize k, we have to take a partial derivative with respect to k and set it equal to 0, which gets us zf’(k_gr) - (n+d) = 0, and in turn, zf’(k_gr) = n + d. From here, just solve for k*

How do you find the golden rule savings rate analytically?

USE THIS KEY EQUATION:
szf(k)=(n+d)k (steady state)

After finding the steady state capital, plug that into szf(k_gr) = (n+d)k_gr, and try your best to solve for s.

What is the golden rule saving rate / golden rule capital

The golden rule saving rate is the saving rate which produces the highest consumption. The corresponding steady-state capital is the golden rule capital.

What is the growth accounting formula?

g_y = g_z + ag_k + (1-a)g_n

Solve for a

How do you find the current period budget constraint?

Set c = Income ± taxes/subsidies - s.

ie: c = y - t - s

How do you find the future period budget constraint?

Set c’ = Income ± taxes/subsidies + s(1+r).

ie: c’ = y’ - t’ + s(1+r)

How do you find the lifetime budget constraint?

First, solve for s in the current period budget constraint.

Next, plug this s into the future budget constraint.

Finally, rearrange the expression so that consumption is on the left and disposable income is on the right, and divide both sides by (1+r)

ie: s = y - t - c
c’ = y’ - t’ + (y - t - c)(1+r)
c’ = y’ - t’ + (y-t)(1+r) - c(1+r)
c + c’/1+r = y-t + y’-t’/1+r

we = y-t + y’-t’/1+r

Where does the endowment point go?

The endowment point corresponds to the situation when the consumer does not save and does not borrow, so s=0. Consumers on the left save, while consumers on the right borrow.

Log-preferences

lnc + θlnc* → max c,c*
s.t. c + Bc* = F

c = 1/(1+θ) * F
c* = θ/(1+θ) * F/B

Perfect Complements

min{c, θc*} → max c,c*
s.t. c + Bc* = F

Set c = θc*
Plug into BC: θc* + Bc* = F
c* = F/(θ+B)
c = θc* = θF/(θ+B)

Perfect Substitutes

c + θc* → max c,c*
s.t. c + Bc* = F

Substitute constraint out: c = F - Bc*
F - Bc* + θc* → max c*
F + (θ-B)c* → max c*
If θ>B, set c* as LARGE as possible.
If θ<B, set c* as _^small as possible.

Rigid Preferences

ⓒ is exogenously fixed constant
c + Bc* = F

ⓒ + Bc* = F
c* = (F - ⓒ) / B
c = ⓒ

One-sided preferences

lnc → max c,c*
c + Bc* = F

c = F
c* = 0

Second Middle Of The Night Equation

c = y - t - s
s = y - t - c

What is the government’s budget constraint in the current period?

G = Nt + B

What is the government’s budget constraint in the future period?

G’ = Nt’ - B(1+r)

How do you find the government’s lifetime budget constraint

First, solve for B in the current period budget constraint.

Next, plug this B into the future budget constraint.

Finally, rearrange the expression so that consumption is on the left and disposable income is on the right, and divide both sides by (1+r)

ie: B = G - Nt
G’ = Nt’ - (G - Nt)(1+r)
G + G’/1+r = Nt + Nt’/1+r

What does a change in the timing of taxes do without market frictions

It moves the endowment point, as the savings change due to tax cuts/tax spikes. The interest rate does not change due to Ricardian equivalence.

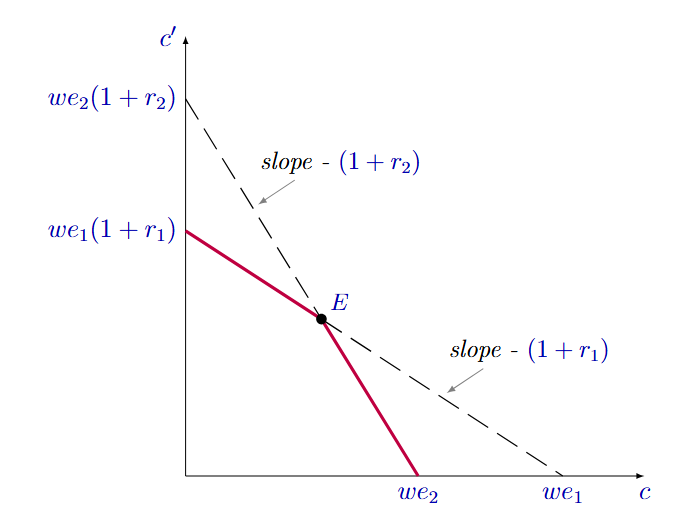
What does a change in the timing of taxes do when the consumer faces two different interest rates, one for lending and one for borrowing?

We get two different we₁ and we₂, one for saving and one for lending. We plot both of these on the graph, where we1 > we2, but we2(1+r2) > we1(1+r1). Then we remove the unattainable points and are left with a kinked graph.

Ricardian equivalence no longer holds, since r1 ≠ r2. This leads to a change in the line AND endowment pine.

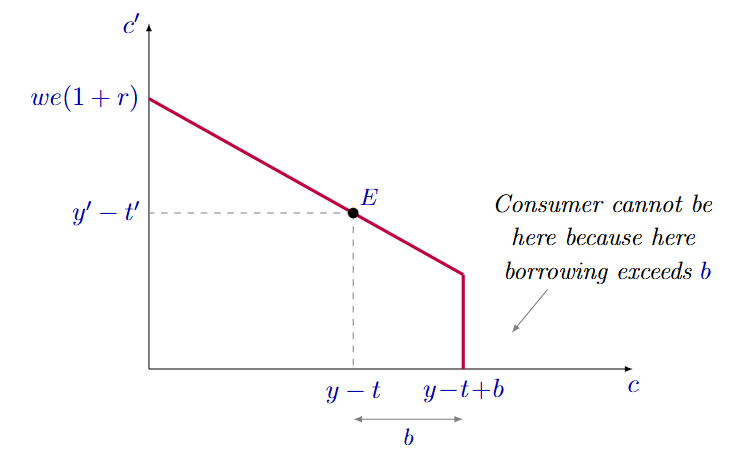
What does a graph with a borrowing limit look like?

It loooks similar to the base two-period model graph, but with a kink at y-t+b, because the consumer cannot borrow more than b.

What is the government budget constraint with Social Security?

Nb = N(1+n)t

How do we know if social security is good or bad for the consumer

we^ss = we + b((n-r)/(1+n)(1+r))

If n (return on social security) is greater than r (return on regular savings), then social security is good for the consumer. If n is less than r, then social security is bad for the consumer.