GEOG 181

Egocentric mental maps

Mental maps of the places we live, work, and visit

Geocentric mental maps

Mental maps of places we have not directly experienced, such as foreign cities

Charts and plans

Specialized documents that are designed to be used as tools by people with necessary training and knowledge, for example: aeronautical charts

General reference maps

Show multiple themes of information - typically used as base maps. Note:

• Small scale maps show more data, but less in detail

• Large scale maps show less area, but provide greater detail and show smaller features

Thematic maps

Generally focus on representing spatial distribution of a single theme of information

Choropleth maps

• Represent the average value of data collected within predefined areas

• Provide a general pattern of the spatial distribution

• Assigns a colour based on a data value to a region

Dot maps

• Provide a general impression of the spatial distribution of a phenomenon

• Require equal-area projections

• Use individual dots to represent a fixed number of something, distributed across space

Proportional symbol maps

• Show the general spatial pattern of a phenomenon

• Symbol is typically shown as a point or a circle, scaled on the value of the attribute

• Good for total quantities, but not for ratios or percentiles

The three functions of maps

1. Navigation

2. Visualization

3. Measurement

Ptolomy

A Greek mathematician whom created the Geographia in the 2nd century, listing coordinates of known locations in the Roman Empire

What were some features of maps that used Geographia?

1. Evidence of the knowledge of a round Earth

2. Use of a projection to transfer the features of a round earth onto a flat map

3. Lines of latitude and longitude

T and O Maps

Represent the European understanding of the world during the medival period (7th century)

What were the three known continents identified on T and O maps?

Asia, Africa, and Europe

Waldseemüller Map of 1507

The most significant map to be created after the knowledge of the “new world”, using projections derived from Ptolomy

Topographic Survey of France

From the late 17th to early 19th century, France undertook efforts to map the entire country, using triangulation, leading to a series of 1:80,000 scale topographic maps

By the 1700s, what development did we begin to see in maps?

Maps began to focus on presenting single themes of data over simple based maps, being used as tools for analyzing spatial patterns

What is the shape of the Earth, and what shape can we use to represent it?

Earth is an oblate spheroid, and we can represent it with an ellipsoid

On the (almost) spherical Earth, we can specify a location using?

1. Latitude

2. Longitude

3. Elevation

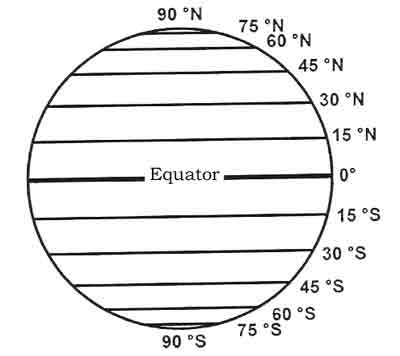
Latitude

Measures our angular position from the centre of the Earth, with respect to the north and south direction

Average length between degrees of latitude

For basic calculations, we assume 111 km

Lines of latitude run ___ to the equator

Lines of latitude run parallel to the equator

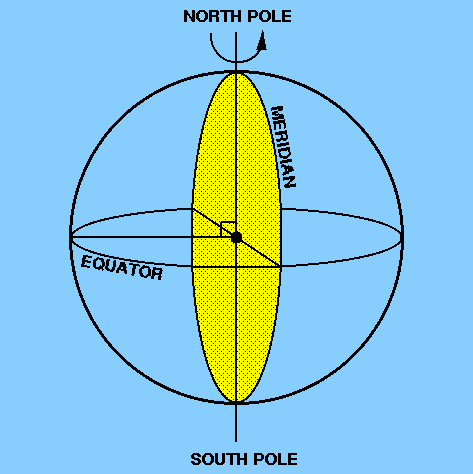
Longitude

Measures our position fro the prime meridian, with respect to the east and west directions

Lines of equal longitude are called

Meridians

Where is the prime meridian located?

Greenwich, England

The length of a degree of longitude at a particular latitude

Length of 1° = 111 km * cos(latitude)

Geodetic datums

Consist of a mesh of reference points which translate positions on maps to their real position on the surface of the earth

1900 U.S. Standard Datum

The first nationwide datum for the U.S., using the Clarke 1866 ellipsoid and had origin point of Meades Ranch, Osborne County, Kansas. Used as the reference points for all points in America from 1901 to 1989

NAD27

In 1927, the original 1900 U.S. Standard Datum expanded to include Canada and Mexico

NAVD29

In 1929, elevations were added to the NAD27

NAD83

In 1983, the NAD83 was created using satellite imagery, based on the GRS 80 ellipsoid. The origin point was the mass-centre of the Earth

Coordinates for points in NAD83 and NAD27 can differ in their location by anywhere from ___ to ___

Coordinates for points in NAD83 and NAD27 can differ in their location by anywhere from 10m to 250m

What replaced NAD83?

The World Geodetic System (WGS84)

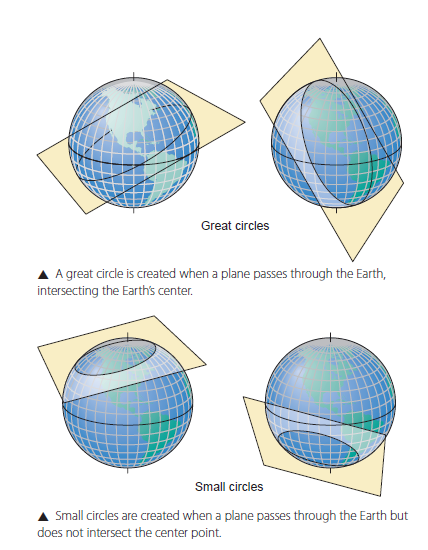
Great circles

The shortest distance between two points on Earth is an arc that is a portion of a great circle

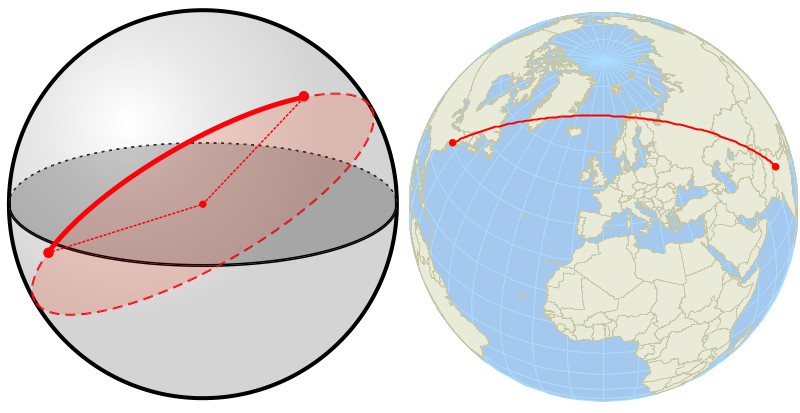
Small circles

Ceated on the Earth when a plane passes through the Earth’s surface without passing through its centre

Great vs. small circles

The plane that creates a great circle passes through the Earth’s centre

The meridians of longitude each represent half a ___ circle

The meridians of longitude each represent half a great circle

The parallels of latitude, other than the equator, are ___ circles

The parallels of latitude, other than the equator, are small circles

Loxodromes

Lines on the Earth’s surface that have a constant compass direction

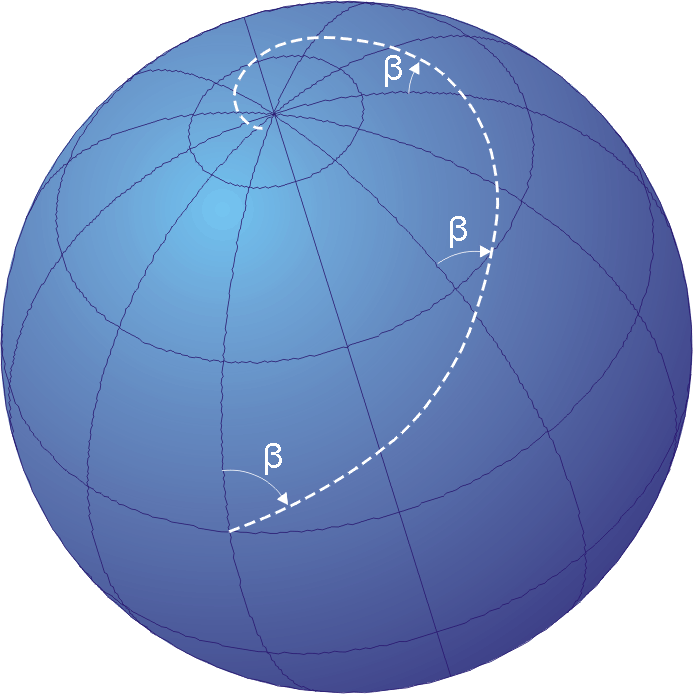
T/F: The meridians of longitude are loxodromes

True, they either head north or south

T/F: The equator is not a loxodrome

False, it heads east or west

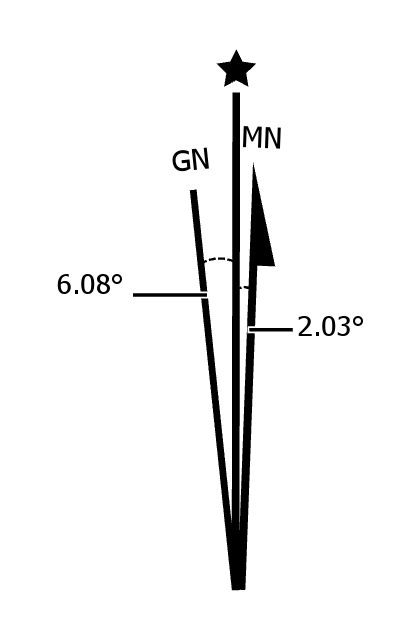
What are the three Norths?

1. True North

2. Magnetic North

3. Grid North

True North

Direction to the North Pole

What North do Meridians point to?

True North and True South

Magnetic North

Direction to the North magnetic pole; the direction that is sensed by a compass

T/F: The Magnetic North is constant

False, it moves around over time

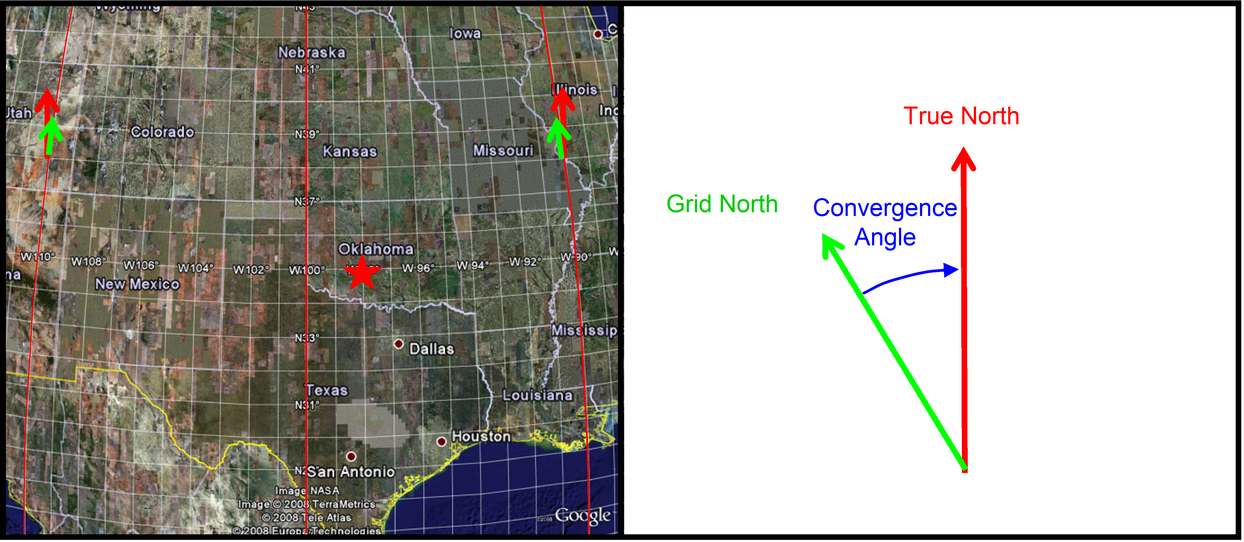
Grid North

North on the Cartesian grid of the UTM projection

T/F: Grid North is the same as True North

False, they diverge as you move away from the central meridian of a UTM zone

Declination diagram

Summarizes the direction relationships between the three Norths on a map

Three steps of creating map projections

1. Create a three dimensional representation of the Earth that has the same area as the surface of the Earth

2. Reduce the scale of the generating globe until it matches the scale of the map

3. Project the features from a generating globe onto the developable surface

T/F: For small scale maps, we can use a sphere for a generating globe

True, a sphere is a good approximation of the Earth over small areas

T/F: For large scale maps, we can use a sphere for a generating globe

False, we must choose an ellipsoid that provides a good fit with the region

Four geometric relationships in projections

1. Equal area

2. Equidistant

3. Conformal

4. Azimuthal

Small scale maps

Cover large regions, such as world maps, continents, or regions

Large scale maps

Show smaller areas in more detail - called large scale since the representative fraction is large (ie. 1:1,000)

Projection class

The type of the developable surface used to produce the final map:

• Plane

• Cylinder

• Cone

• Conventional (use mathematical rules)

Projection aspect

The orientation of the projection surface with respect to the generating globe:

• Normal (most common)

• Transverse

• Oblique

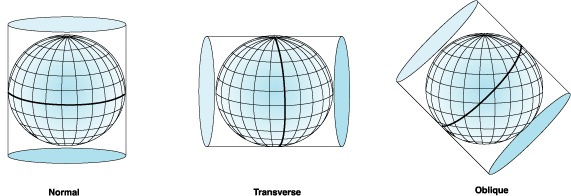
Normal projection aspect

The axis of projection is lined up with the axis of the generating globe

Transverse projection aspect

The axis of the projection is perpendicular to the axis of the generating globe

Projection case

The position of the projection surface relative to the surface of the generating globe:

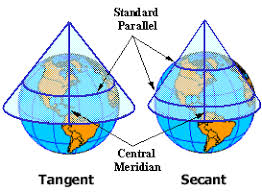
• Tangent

• Secant

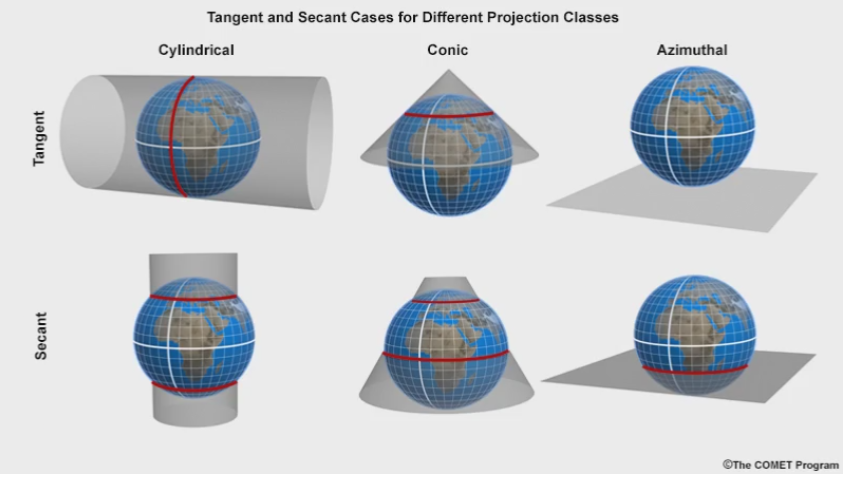
Tangent case

The projection surface lies tangent to the generating globe

Secant case

The developable surface intersects the generating globe

Standard points (or lines)

The point or lines where the projection surface touches the generating globe

The further we move away from the standard point or lines, the ___ distortion there is

The further we move away from the standard point or lines, the more distortion there is

Azimuthal projection

• Created by projecting onto a flat plane

• Preserves directional relationships about the standard points or lines

• Useful for polar regions

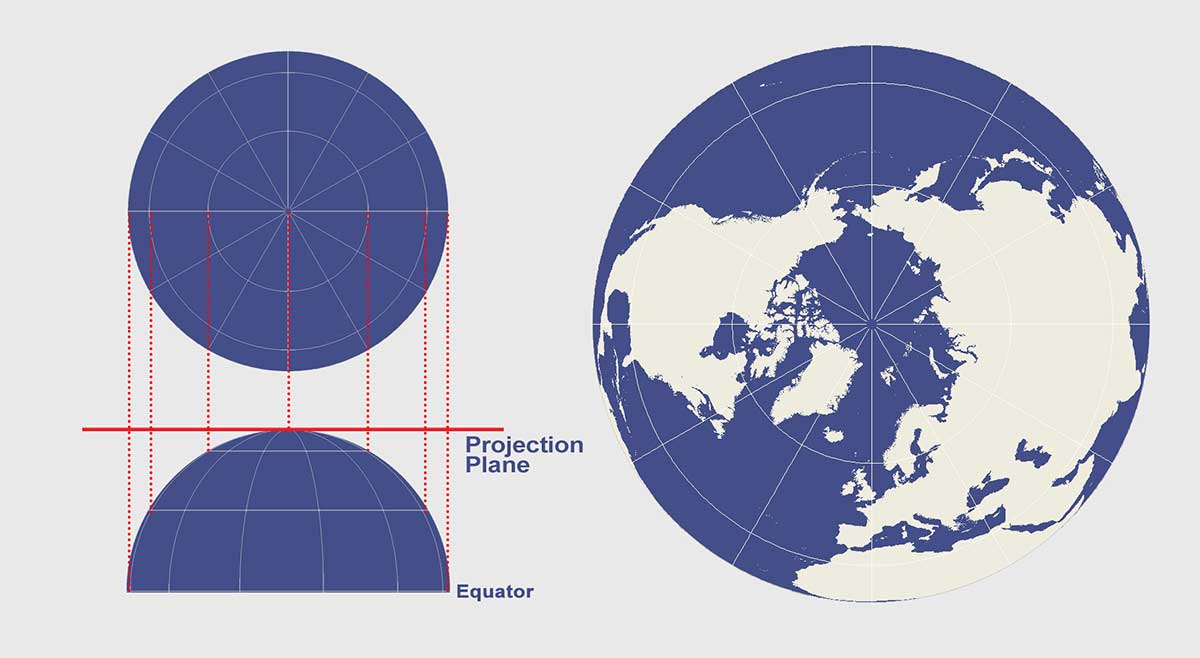
Gnomonic projection

• Azimuthal projection

• Great circles appear as straight lines

• Useful for navigation

Stereographic projection

• Azimuthal projection

• Preserves the shapes of features

• Not possible to show more than one hemisphere

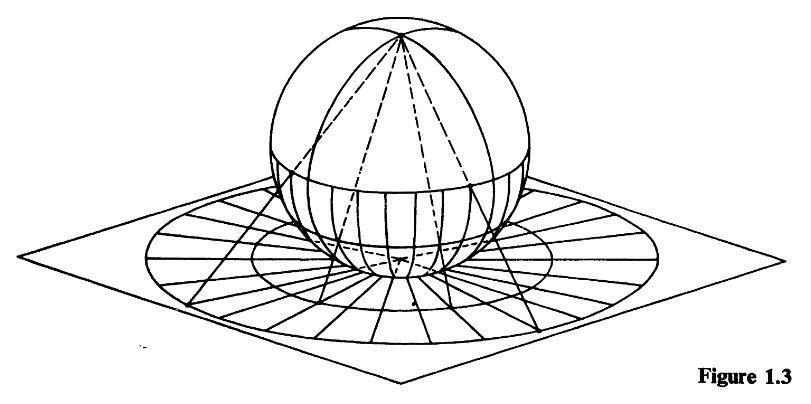
Orthographic projection

• Azimuthal projection

• Provides a view of Earth as it appears in space

• Not possible to show more than one hemisphere

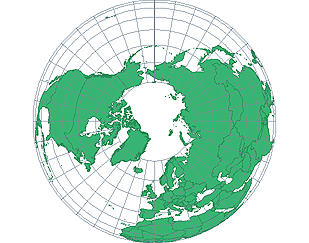
Azimuthal equidistant projection

• Constructed mathematically

• Preserves angular relationships around the standard point

• Preserves distances measured from the standard point at the centre of the map

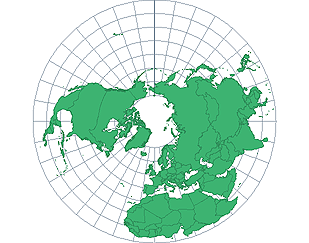
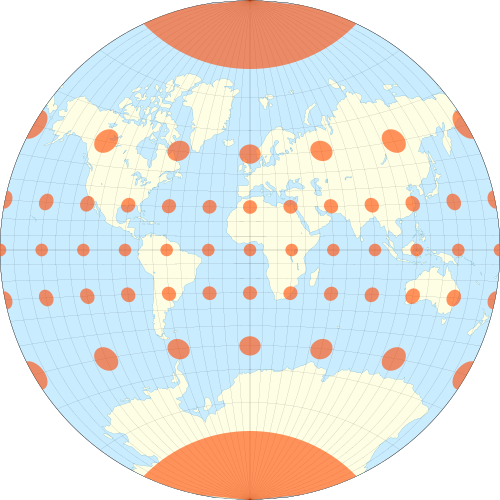
Lambert Equal-Area (azimuthal)

• Capable of depicting the entire surface of the Earth

• Preserves area

• Heavily distorts shapes

Cylindrical projections

Created by wrapping a cylinder around the generating globe

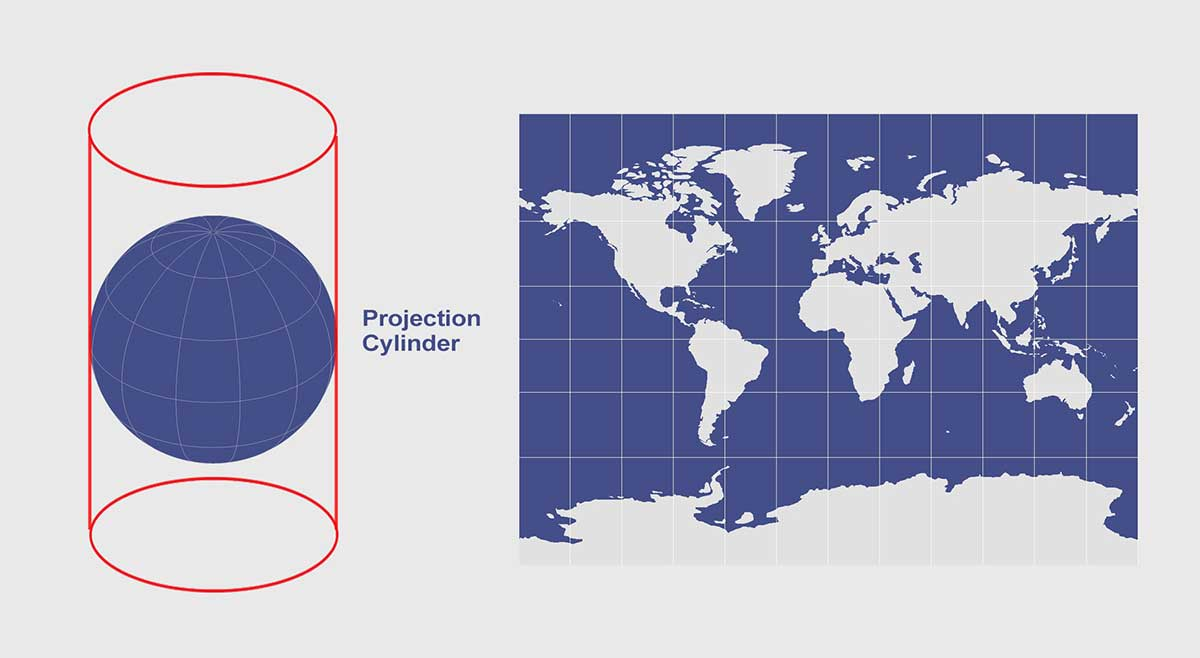
Lambert Equal-Area (cylindrical)

• Standard line runs around the equatorial region

• Preserves area

• Heavily distorts shapes

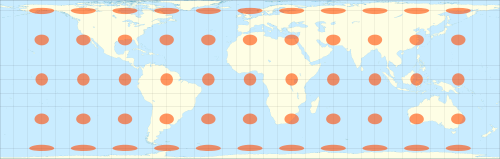
Equidistant projection

• Cylindrical projection

• Preserves north/south distances, as well as the standard lines

• Distorts shape and area

• Sometimes called “unprojected” (wrong)

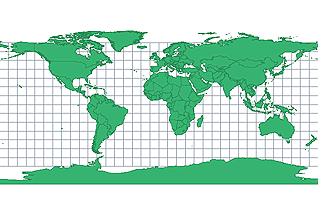
Sinusoidal projection

• Cylindrical projection

• Preserves area

• Preserves east/west distances

• Parallels of longitude are proportional to their lengths on Earth

Mercator projection

• Cylindrical projection

• Most famous projection

• Preserves angular relationships

• Preserves shapes of features

• Heavily distorts area

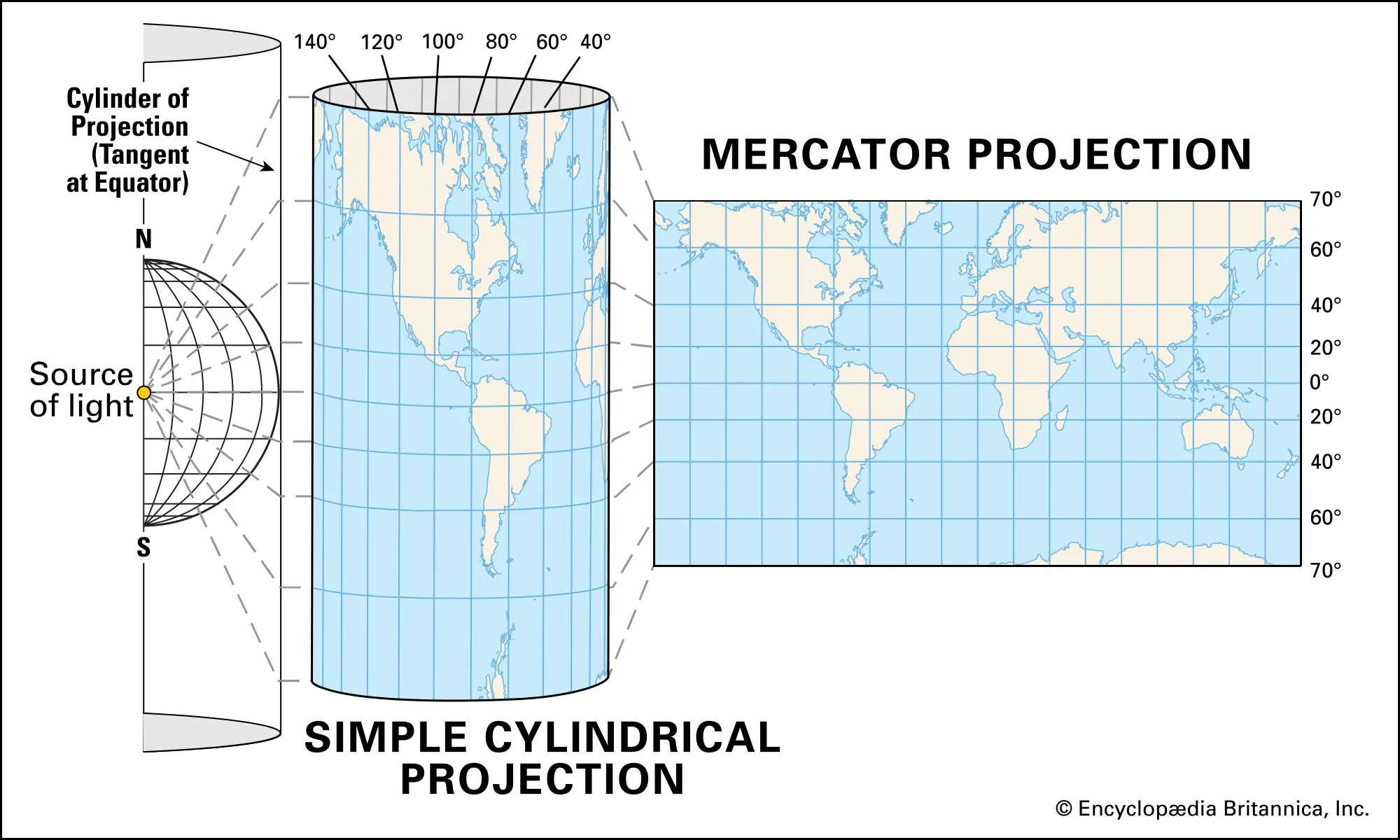
Why is the Mercator projection still so heavily used?

1. Loxodromes appear as straight lines, allowing for sailors to plot courses easily

2. Angles and shapes are preserved locally, meaning that intersections intersect perpendicularly on the map

3. Lines of longitude and latitude create perfect rectangles

Compromise projections

Do not preserve any geometric relationships, but instead strike a balance between each to make them well-suited for global mapping

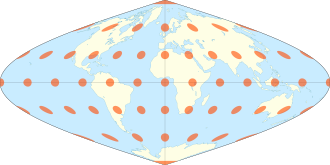
Van der Grinten projection

• Compromise projection

• Projects the entire Earth onto a circle

Robinson projection

• Compromise projection

• Strikes a balance between preserving shape and area

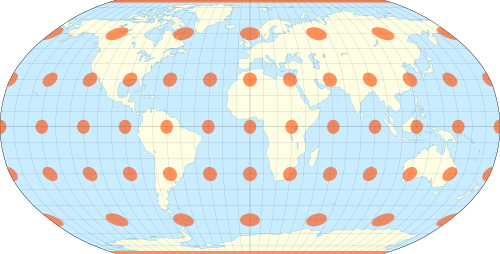
Winkel Tripel projection

• Compromise projection

• Contains less distortion of land masses near the poles

• Still widely used today

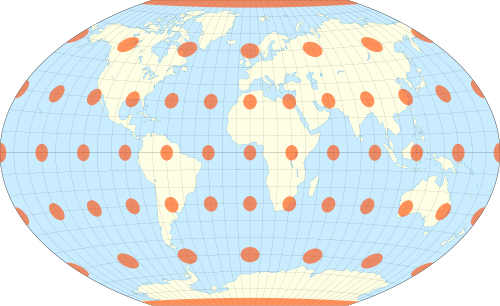
Conic projections

• Often used to depict mid-latitude regions

• Ptolemy’s maps used many conic projection characteristics

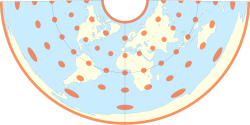
Equidistant conic projection

• Distances measured along meridians and standard lines are true to scale

• A rudimentary version was described by Ptolemy

Lambert Conformal Conic projection

• Conic projection

• Preserves shape of features

• Widely used for aeronautical charts

• Straight line drawn on this projection approximates a great circle route

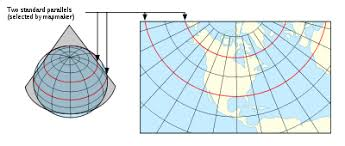
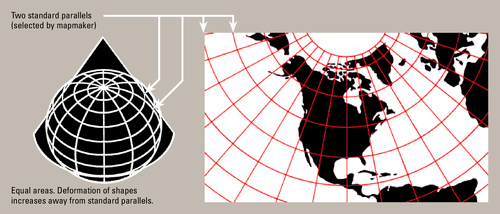
Albers Equal Area projection

• Conic projection

• Preserves area

• Commonly used in Canada and United States

We consider two things when selecting an appropriate projection

1. The purpose of the map

2. The area of interest that we wish to map

Best projection for dot density maps

An equivalent (equidistant) projection that preserves area

Best projection for navigation maps

Gnomic projection for polar regions, or Mercator projection

Best projection for polar regions

Azimuthal projections

Best projection for mid-latitude regions

Conic projections

Best projection for equatorial regions

Cylindrical projections

Best projection for global maps

Compromise projections

Best projection for showing areas of deforestation globally across 10 years

Sinusoidal projection, since it preserves area

Best projection for a dot map showing zebra populations in Africa

Sinusoidal or Lamert Equal-Area, since they preserve area and equatorial regions are relatively undistorted

Best projection for showing areas of deforestation in South America

Albers Equal Area, since it preserves area and reduces distortion in mid-latitude regions

Best projection for showing state-by-state Coronavirus rates in the U.S.

Albers Equal Area, since it preserves area and reduces distortion in mid-latitude regions

Best projection for displaying navigational routes in Antarctica

Gnomonic projection, since it is azimuthal (good for polar regions), and straight lines on a map create a great circle route

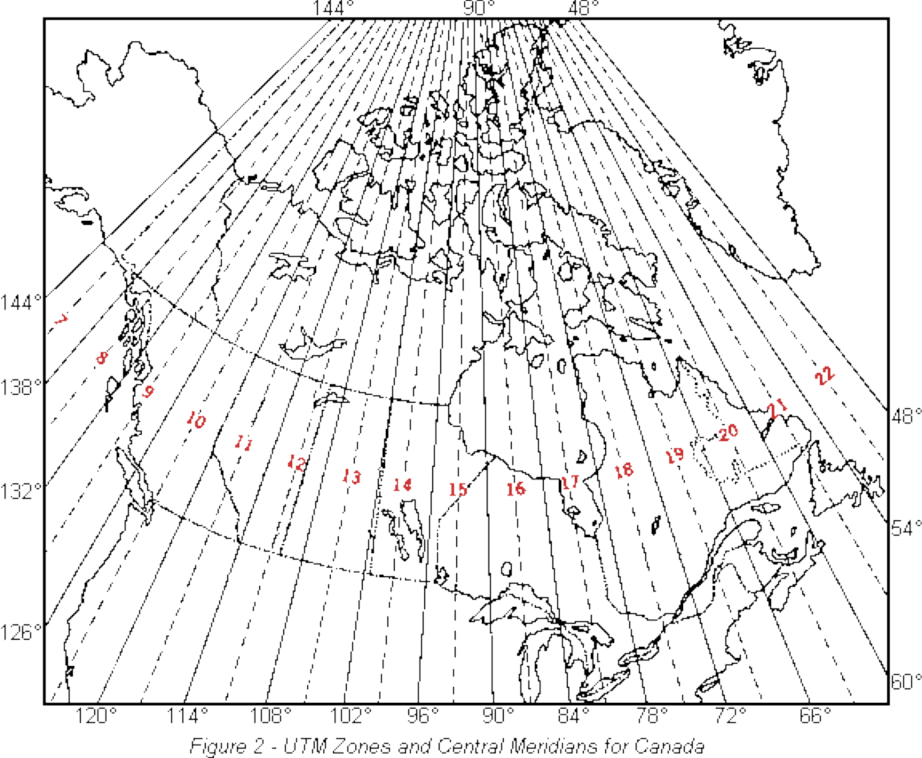
Universal Transverse Mercator Projection

• Compromise projection that uses a Cartesian grid of coordinates

• Most commonly sued for localized mapping

• Comprised of 120 individual projections

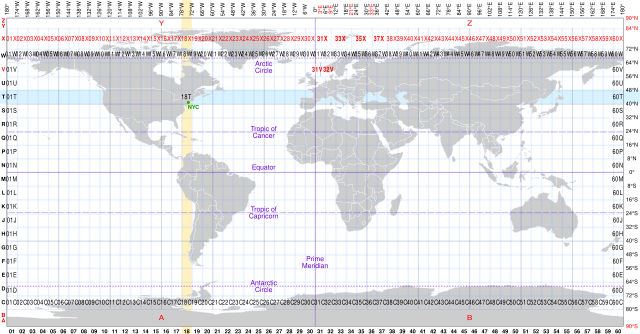
Cartesian coordinates in UTM

Each hemisphere in each UTM zone has a Cartesian grid based on a false origin point for that half of the zone, with coordinates (0, 0)

Map accuracy

How closely the information on a map matches the true value: can be scale-specific and application-specific

Map precision

How the numerical and categorical data in the math is being measured

The two types of errors in geospatial data

1. Systemic error

2. Random error