Multivariable Calculus Formulas, definitions properties and use cases

ellipsoid

x²/a² + y²/b² + z²/c² =1

has a constant

a=b=c means it’s a sphere

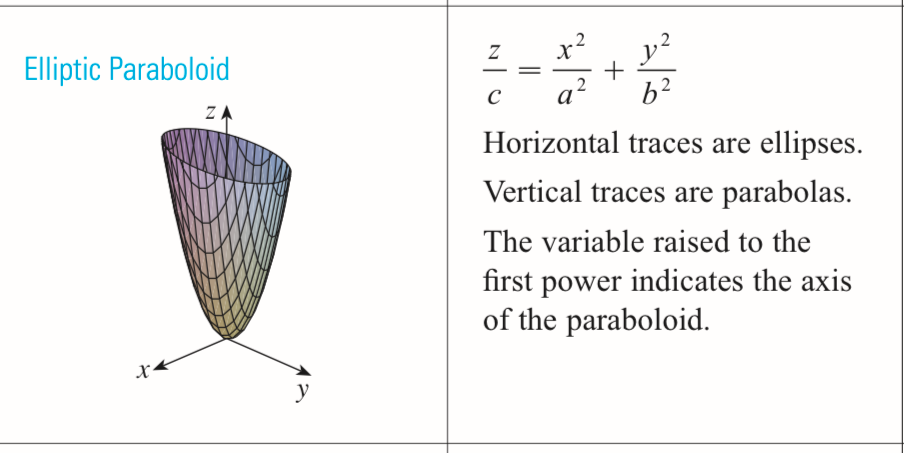
elliptic paraboloid

x²/a² + y²/b² = z/c

z/c is not squared

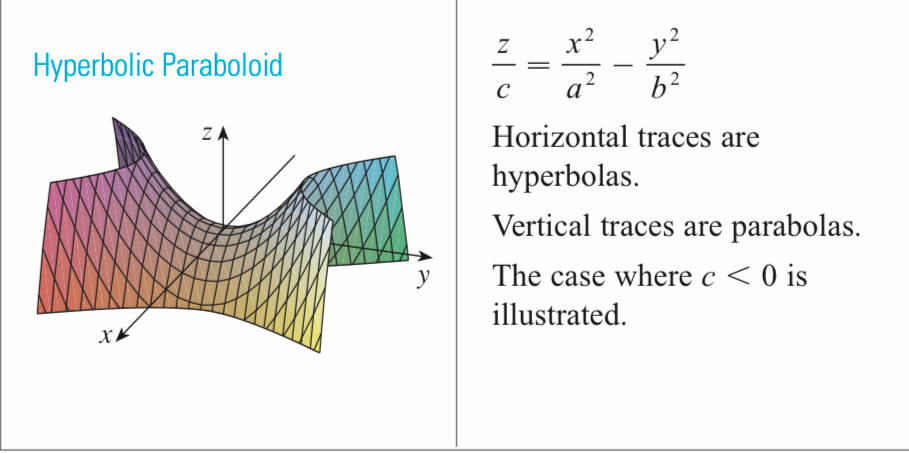
hyperbolic paraboloid

x²/a² - y²/b² = z/c

“hyper = negative”

z/c is not squared

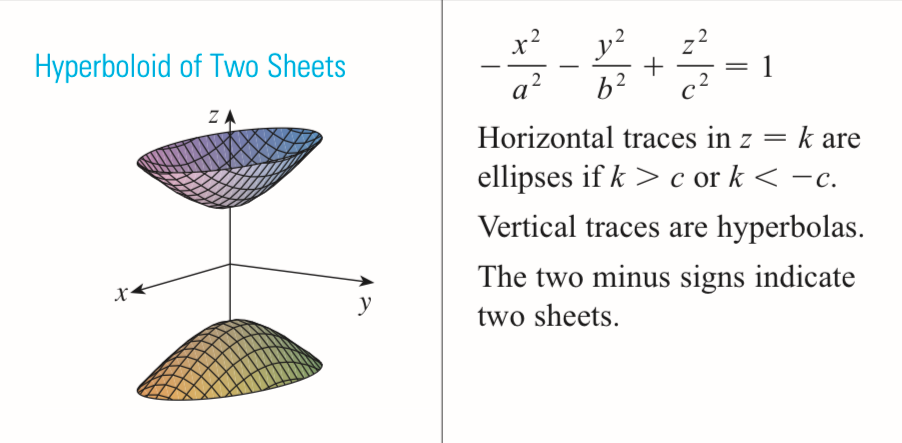
hyperboloid of two sheet

-x²/a² - y²/b² + z²/c² = 1

has a constant

always two negatives

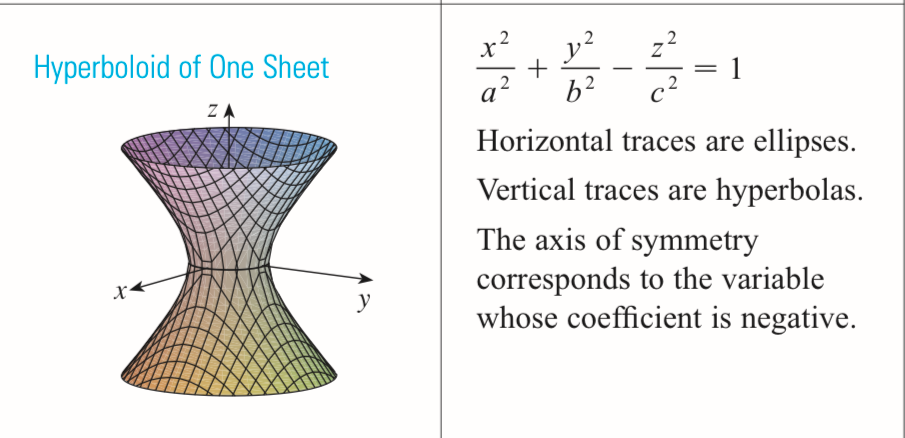
hyperboloid of one sheet

x²/a² + y²/b² - z²/c² = 1

has a constant

always one negative

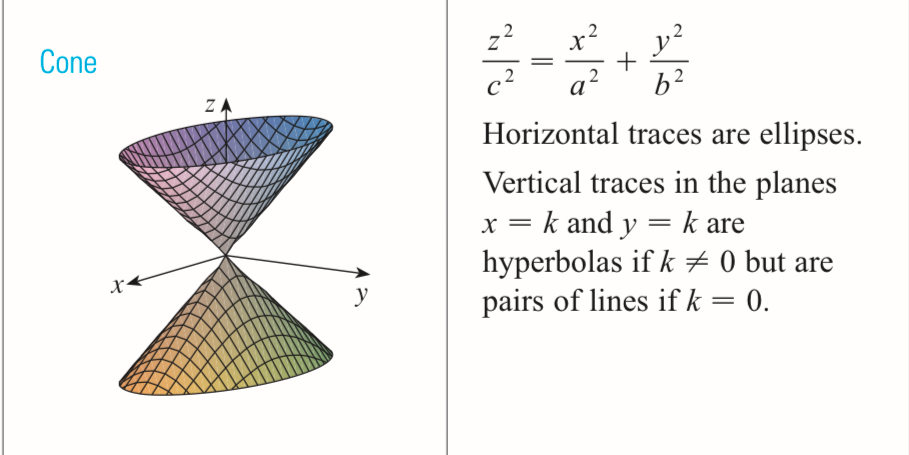
Cone

x²/a² - y²/b² = z²/c²

doesn’t have a constant

can be mistaken for hyperbolic paraboloid or hyperboloid

circular cylinder

x²-y²=1

only ever has two variables

parabolic cylinder

z=x²

only ever has two variables

| P₁ P₂ | =sqrt { (x₂-x₁)^² + (y₂ -y₁)² +(z₂-z₁)² }

distance formula between two vectors

magnitude formula

|a|=sqrt(x² +y² +z²)

Vector direction

The letter that comes first, it’s the tail (initial point)

The letter that comes second, it’s the tip (terminal point)

all vectors but the zero vector have direction

Triangle law

AB(vector) +BC(vector) = AC(vector)

Scalar Multiple

C * vector

c stands for constant in this case

Scalar Multiple properties

c>0 same diction as vector

| c * vector| = c * |vector|

c<0 opposite direction of vector

| c * vector| = |c|* |vector|

c stands for constant in this case

Parallelogram Law

The parallelogram law states that the vector sum of two vectors is equal to the diagonal of the parallelogram formed by those two vectors. This means that if you place the tail of one vector at the head of the other vector, the diagonal of the resulting parallelogram represents the vector sum.

how find a vector from two points

P(1,2,3) and R(3,2,1)

Vector PR would be found by taking x, y and z values of R and minus the x, y and z values of P

PR=<2,0,-2>

adding vectors (triangle law in action)

a=< 5 ,- 12 > b=< -3 , -6 >

a+b = < (5 - 3) , (-12 -6) >=< 2 , -18 >

if the vectors have coefficients

2a+ 3b

first multiple the x,y,z values by the coefficients

2a=<10 ,-24 > and 3b=< -9 , -18 >

and then add them

To find a Unit vector that same given direction as the given vector

example v=8i-j+4k

find the magnitude

|v|=sqrt ( (8)² +(1)² +(4)²)= 9

then divide the vector by the magnitude

v/|v|= 8/9 i - 1/9 j + 4/9 k

Dot product Geometric Definition:

a⋅b=∣a∣∣b∣cos(θ)

Dot product Algebraic Definition:

a⋅b=a_x​b_x​+a_y​b_y+a_zb_z

Properties of dot product

• a ⋅ a = |a|²

• a ⋅ b = b ⋅ a

• a ⋅ 0 = 0

• a ⋅ (b+c) = a ⋅ b + a ⋅ c

• Ka ⋅ b = K (a ⋅ b) = a ⋅ Kb

K= constant

a ⋅ b = 0

the vectors are perpendicular

Directional angle Cos α

a_x/|a|

Directional angle Cos β

a_y/|a|

Directional angle Cos γ

a_z/|a|

Cos² β +Cos² α + Cos² γ =1

property of Directional angles

If two vectors are parallel

they are scalar multiple of each other

To find actual directionals angles on a calculator

use inverse cos on the calculator

cross product

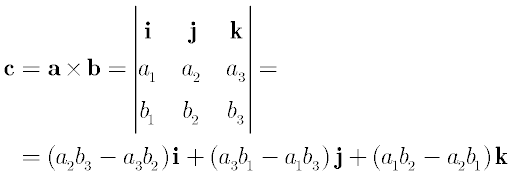
triple product

just replace i, j, k with the third vector

properties of the cross product

• a x b = -b x a

• a x (b + c) = a x b + a x c

• Ka x b = K( a x b ) = a x (Kb)

• a ⋅ (b x c) = ( a x b ) ⋅ c

• a x b is perpendicular to a and b

Volume of parallelepiped determined by three vectors

V= | a ⋅ |b x c||

the bars mean absolute value

area of parallelepiped

|a x b|

area of a triangle

|a x b| / 2

the bars mean magnitude

parametric equation of line

through point p₀(x₀,y₀,z₀) and parallel to vector <a,b,c>

x=x₀+a t y=y₀ + b t z=z₀ + c t

Symmetric equation of a line

x-x₀/a = y-y₀/b = z-z₀/c

if a,b or c = 0, x=x_{0 ,} y-y₀/b = z-z₀/c

Plane equation

n ⋅ ( r₁ -r₀) =0

let n=<a,b,c> , r_0=<x_0,y_0,z_0> and r= <x,y,z> any point of the plane

a(x-x₀)+b(y-y₀)+c(z-z₀)=0

ax+by+cz - (ax₀+by₀+cz₀)=0

ax+by+cz+d=0

distance formula between planes and points and other planes

D= |n ⋅ b| / |n|