Chapter 8: Forecasting

What is the purpose of forecasting?

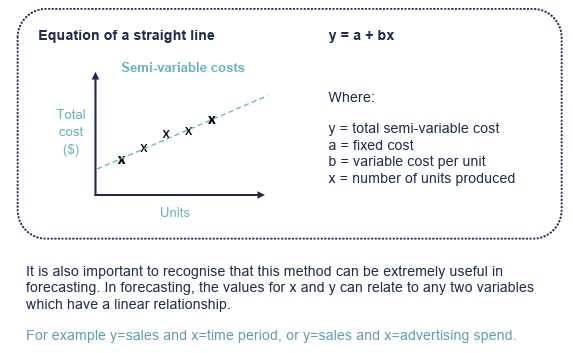
What is the equation of a straight line in when breaking down semi-variable costs and what do the variables stand for. What does the graph look like? Is this useful for forecasting?

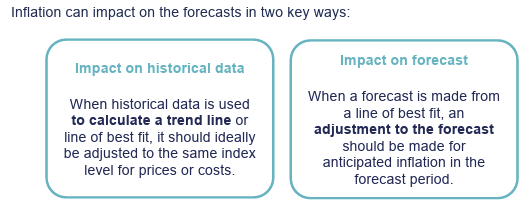
The accuracy of forecasting is affected by the need to adjust historical data and future forecasts to allow for price or cost inflation.

What are the two key areas inflation has an impact on forecasts?

What are the two methods of adjusting inflation:

• Percentages

• Index numbers

What is linear regression? What is the key rule that always applies?

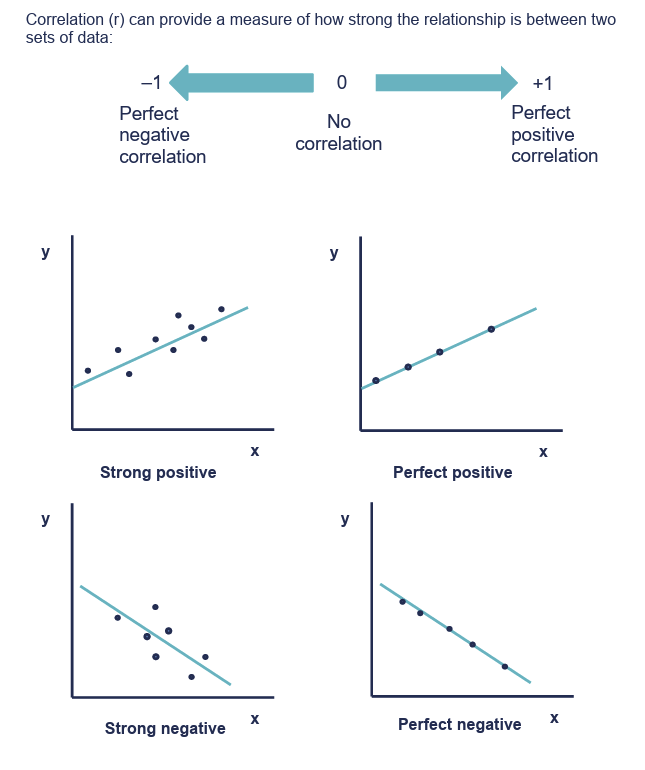
What does correlation provide a measure of?

What would the numbers -1,0 and 1 show?

What does the coefficient of determination show and how is it calculated?

What are some limitations of linear regression analysis?

“Only interpolated forecasts tend to be reliable” - 📊 Example

Suppose you use linear regression to model the relationship between study hours and exam score, based on data from students who studied 0 to 10 hours:

Hours Studied	Exam Score
0	50
2	60
5	75
8	85
10	90

Let’s say the regression line is:

Score=50+4×Hours\text{Score} = 50 + 4 \times \text{Hours}Score=50+4×Hours

---

✅ Interpolation

If you predict the score for someone who studied 7 hours, you're interpolating:

Score=50+4×7=78\text{Score} = 50 + 4 \times 7 = 78Score=50+4×7=78

This is reasonable, since it's within the data range (0 to 10 hours).

---

❌ Extrapolation

If you use the same model to predict the score for 20 hours of study:

Score=50+4×20=130\text{Score} = 50 + 4 \times 20 = 130Score=50+4×20=130

But an exam score can't go beyond 100%, so this prediction is unrealistic. The model assumes the same trend continues forever, which is not valid outside the original data range.

What is time series analysis?

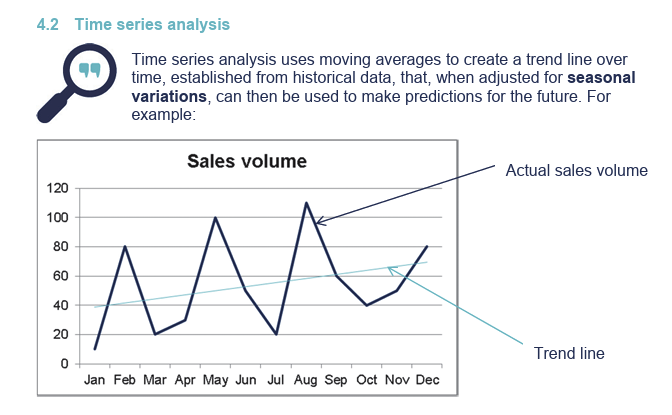
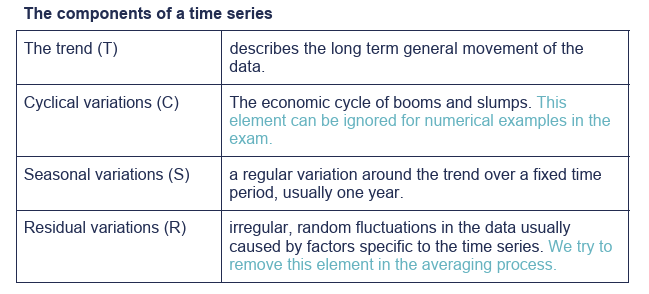
Explain the components of a time series:

• The trend

• Cyclical variations

• Seasonal variations

• Residual variations

What are the 3 ways of calculating the trend? Explain what the last method attempts to do.

How are seasonal variations estimated? What happens when the actual value is higher/lower than the trend line value? What should seasonal variations add up to?

How are time series used to forecast prepared under the additive model and the multiplicative model?

What are some of the limitations of time series analysis?