Review-Ch 11 statistics

Inference for regression

T statistic (for regression line)

• tests whether the slope of the true regression line is 0

  • if rejecting that the slope of the true regression line is 0 → regression line will be useful in PREDICTING y given x

  • if not rejecting → plausible that the positive/negative trend seen is solely due to CHANCE variation that ALWAYS results when you have ONLY 1 sample

Confidence Interval(regression line)

• helps to DECIDE whether the linear relationship is statistically significant & practical significance

  • ___the average increase/decrease in___population

• If claim is not in the interval →not supported claim

If Confidence interval has…

• All positive values → evidence for positive association

• All negative values → evidence for negative association

• BOTH positive and negative values → no evidence for an association

B₁

the slope of the true regression line

B_o

the y intercept

B_IO

Hypothesised slope

b₁

slope(estimate from a sample)

df(regression line)

n-2, because a sampling distribution is a t-distribution

S: Standard error(regression)

• spread around the regression line

• the difference BETWEEN predicted(estimates) and the actual scores are measured with this residual standard deviation

SSE

Sum of squared errors

Slope(Interpretation)

• for every 1 increase/decrease in x, there is a predicted increase/decrease in y

• The slope(* correlation sign is same as slope sign) of a regression line is in the middle of the Confidence Interval

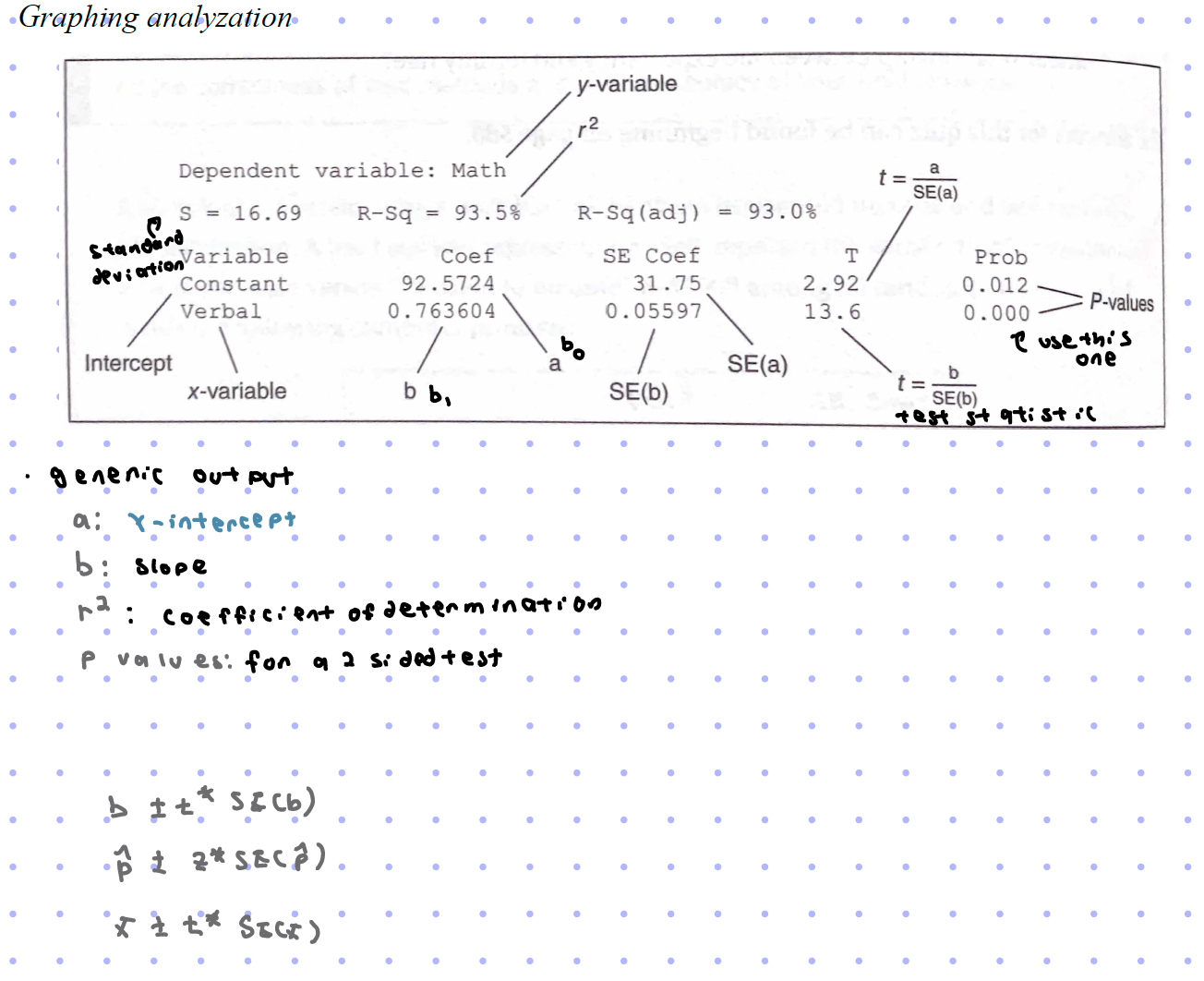
r

Correlation coefficient, can be from -1 to 1

r²

coefficient of determination

• “__% of the variation in y can be attributed/accounted for by the variation in x

Significance Test(Regression line)

CONDITIONS

1. approximately normal distribution of y for a fixed value of x…

• The means lie on a line

• Standard deviation is CONSTANT across ALL x values

2. ONE of below

   1. SRS from a bivariate(2) population

      OR

   2. independent random sample with ( x,y ) values given

3. roughly linear scatterplot

4. Residual plot has no pattern/curvature

5. Residual distribution looks approximately normal or uniform(on x axis ALONE)

STEPS

name test: t-test for the slope of a population regression line

1) Conditions

2)Hypothesis

let B represent the slope of ___between x and y

H_o: B=0

H_A: B≠,<,> 0.

3) Test stat, p-value

t=(b₁-BIO)/sb₁

_4)COnclusion

• smaller p value→STRONGER evidence against the null hypothesis bc farther from α → “sufficient evidence”

Confidence Interval(Regression Line)

CONDITIONS

1. approximately normal distribution of y for a fixed value of x…

• The means lie on a line

• Standard deviation is CONSTANT across ALL x values

2. ONE of below

   1. SRS from a bivariate(2) population

      OR

   2. independent random sample with ( x,y ) values given

3. roughly linear scatterplot

4. Residual plot has no pattern/curvature

5. Residual distribution looks approximately normal or uniform(on x axis ALONE)

STEPS

1) Conditions

2) Computations

CI=b₁+- t* sb₁

df= n-2

t*=invt(% thingy, df)

3) Interpret in Context

“We are __% sure that the true slope of the line of regression between x var and y var lies BETWEEN the interval ( , )”

“Out of 100 such Confidence Interval, when constructed from random samples. The expected true value B₁ to be #(as a number) of them”

line of mean/averages

u_y=b_o+ b₁x

Variability

size of on depends on…

1. Sample Size(n)

2. Variability in y

Standard error

The slope varies less when…

1. Sample size larger

2. values of y tend closer to the regression line

3. values of x more spread out

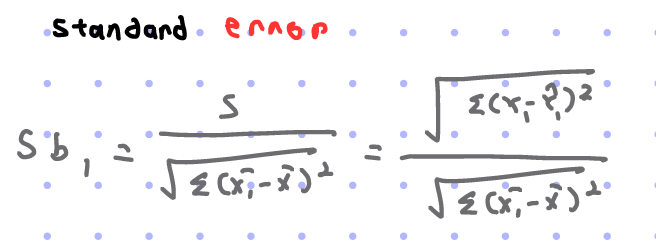
Power transformation

y=ax^b

^{the base is what changes}

(log x, log y)

Exponential model

y=ab^y

^{the exponent is what changes}

( x, log y)

Ln transformations

(ln x, ln y)

• the LSRL is ln(y var)=a+b(ln(y var)

  which also EQUALS y var=e^a+x^b

“Cubic or more” transformation

• see if Confidence Interval capturers 3(n) or not

• CI could potentially be too big/small

General conclusions

• if the slope was actually B_IO only a (p-value number) chance of getting a slope as far or FARTHER than b₁ is from B_IO for an SRS of units

• if a transformation is made→include it in the LSLR equation & conclusion

Graphing Analyzation

Scatterplot

• If there are gaps/empty space in _the middle suggest 2 clusters→ If analyzed separately could result in other answers

Graphing calculator

• if H_A is 1 sided→p value on calculator graph /2

• S=standard deviation

• constant(intercept) coef= bo

• x variable coef =b1$