MATH formulas and ideas

Exponential minimum

dont have one

exponential maximum

is found only when decaying (.25)^x and is always zero

Density =

Mass/volume

quadratic minimum

our y/k value

quadratic with no solution

when D < 0 (a negative number)

quadratic with two solutions

when D>0

linear equations can have

one solution, no solution, or infinitely many solutions.

linear: infintley many solutions

slope AND y-intrecept/b are the same

linear: no solution

slope is the same but y-inter/b is different

linear: one solution

the slopes are different, indicating that the lines intersect at exactly one point.

discriminant formula

b²-4ac

when to use vertex formula of a quadratic

in a physics like question where it is being thrown/ dropped

quadratic x value minimum

is the h value but usually isnt referred to as minimum unless the question asks so

quadratic h value

x-coordinate/value (ex. seconds) at the min/max

the vertex value A s equal to

a TIMES (x²+bx+c)

how to find the A value in vertex quadratics

find a coordinate mentioned, using the given vertex, plug in the formula and solve

porabola opens upwards

a is positive

parabola opens downwards

a is negative

ur given a vertex quad told to find a with only a

write out the vertex formula and distribute then also distribute a, with additional information ur overall just substituting

what could be the factors of p

were asked for the roots of the function p

how to find roots (ina vertex quad function)

using midpoint formula x1+x2/ 2 =h

or

solving for x when y is zero

predicted to increase by n%, n is?

(1-r) after finding the rate remember to subtract one to find %

arc length/radius

CENTRAL ANGLE = radian

arc length/circumfrence

CENTRAL ANGLE = theta /360

arc measure

is the central angle

arc length (degrees)

theta/360 × 2pie(R)

circumference of a circle

2pie(R)

sum of roots

-b/a

radian/degree conversion

r=degree(pie)/180

sin x complimentary rule

= cos(90-x)

where cos’s x + sins’s x = 90

sin x = degree, find the sides of the tri

degree → fraction → O/H

line tangent to the circle =

slope perpendicular to radius

90 degree angle

product of roots

c/a

eq of circle

(x-h)² + (y-k)² = r²

sector area

theta/360 x (pie)r²

cannot be a tri similarty

ASS

total interior angle

180(n-2)

tri similarity ratio

short/long = short/long

when presented w two tri

similairty question

if given a 45/90/45 0r 90/60/30 info or square roots in the answer choice

always the subject to be used

Coordinate Distance

/ square root (X2-X1)² + (Y2 - Y1)²

3:4:5 ratio tri

we’re dealing w a right triangle

Ex. 9:12:15

Volume of cube

S³

Bisector proof

Can never stand alone and be enough proof to find the shape

# of vertices =

Number of sides

Cylinder volume

Pie x R² x h

triangular (cylinder base) volume

1/3(pie, r²) x H

Volume of sphere

4/3(pie)R³

(POWER OF 3)

Area of trapezoid

1/2(top + bottom length) x H

Mass =

Density x Volume

Triangular prism Volume w 2 other triangles

½ Base area x height

SA of cube

6s²

SA of cylinder + of only the middle part

h x 2pieR → (middle)

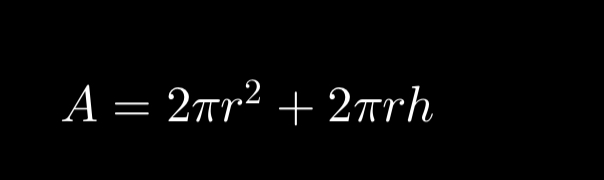
Triangles are congruent

They are the exact same

Triangles are similar

Have a relationship but aren’t exactly the same

sector area

theta/360 x pieR²

(as a central angle) pie =

180

volume of right square prism

(square base, rectangle prism)

x² x h

find arc length, with one given and its degree

arc length unknown/ arc length = theta new/ theta old

corresponding angles in similarity tri

are congruent

completing the square

x² + 12x + #

how to complete the square

Bx/2 = # → #²

if the absolute eq. is originally = to a negative number

no sol.

3|x+1| + |x+1| =

4|x+1|

discrminant is used in two ways

1) linear and quadratic system

2) a quadratic alone

positive constant

b² = ± 6 → choose 6

“which pair is a solution to the eq.” W MULTIPULE CHOICE

plug into system and make a given # the variable

system of eq. problem, check 1st

only quad? only linear? or both?

leave no square roots b4 assuming

y is decreasing by 0.5

linear decline

y halves as x increases

exponential decline

a constant

non-changing #

a fixed #

“doubles everyday”

geometric seq. (multiplying)

initial(1-r^n) / (1-r)

addition sequence

initial((n-1) x D)

d is amount we are continously adding with

multiplying sequence

initial(1-r^n) / (1-r)

smallest solution

(quadratic)

out of the two possible sol. which is smaller

(2/35)/2

1/35

absolute expression

do the ENTIRE process then apply the absolute

watch out for disriminant when working w C

switching of signs due to division

how to avoid discreminant swap

ensure ur -4 has a negative c or a and not both

decreasing rate is found between

-1< r <0

5 turn into a fraction over x

5y/y → y/y x 5

squaring anything has two sol.

making ± 100 a viable answer

esp. for quadratic answers

“find the solutions”

find the roots/ solve for x(‘s)

quadratic intervals

found in the factored form (x+1), -1 is part of the interval

“sum of solutions” but for non-quadratic

add both possible answers (x+y)

“shown as a constant/base/cofficent”

look for the answer in the eq as what is asked

big fractions 1st step

as much factoring as possible

zero-product property

if the product of two numbers equal zero, one or the other must be 0

x-1= ax + b

the eq can be taken quite literal since variables match up and structure

(ax = x so a =1)

poynomial divison 1st check

are all the remainders the same?

remainder theorm

the remainder is found inserting into our eq x’s of the quadratic, c, (from x-c)

if told add a quadratic

assume ax² + bx + c

if talking abut quad. but theres no mentioning of being thrown up or being propelled

refer to a regualar quad formula

the function = 0 when x equals 0

indicates no c value

extract c from 2(x+5)(x-6)

(2×5) x -6 = C

b² > 6400

two possible solutions due to ± 80

b² < 6400

-80 < b < 80

maximum exponential w change in domain

if x>/= 1, our maximum is now 1 and is plugged into eq to find that ones specific max

edges of a cube

same as side

function tables can be

quad, exponential, linear, sequential, exponential w a linear power