Honors Algebra 2 Review

Exponential Growth

A=P(1+r)^t

Exponential Decay

A=P(1-r)^t

Exponential Growth

A=P(1+r)^t

Exponential Decay

A=P(1-r)^t

Compound Interest

A=P(1+r/n)^nt

Half-Life Formula

A=P(1/2)^t/h

Continous Growth

A=Pe^rt

Product Property of Logarithms (Log(b) mn)

Log(b)m + Log(b)n

Quotient Property [log(b)m/n]

Log(b)m-log(b)n

Power Property log(b)m^n

nlog(b)m

Change of Base log(b)a

[log(x)a]/[log(x)b]

Sine

y/r

Cosecant

Opposite of Sine r/y

Cosine

x/r

Secant

opposite of cosine r/x

Tangent

y/x

cotangent

opposite of tangent x/y

What is the term for trig func in each quadrant (each one includes reciprocals of the other)

All Students Take Calc

30 60 90 triangle

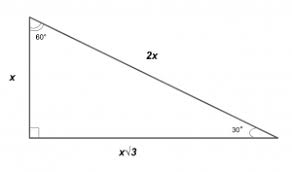
45 45 90 Triangle

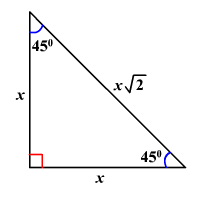
Sin/Cos

Tan

Cos/Sin

Cotangent

1/sin

csc

1/cos

sec

1/tan

cot

sin²+cos²

=1

1+cot²

csc²

tan²+1

sec²

n(A or B)

n(a)+n(b)

nPr

n!/(n-r)!

nCr

n!/(n-r)!r!

Confidence Interval

sample mean +- z*(standard deviation/square root of n)

90% (z*)

z* 1.64

95% (z*)

z* 1.96

99% z*

z* 2.58

margin of error

+- z*(standard deviation/square root of n)

z*

[x-mean]/standard deviation

Arithmetic Explicit

A(n)=a(1)+d(n-1)

Finite Sum Arithmetic

S(n)=n/2 * [a(1)+a(n)]

Geometric Explicit

A(n)= A(1) * R^(n-1)

Finite Sum Geometric

S(n)= [A(1) * (1-r^n)] / 1-r

Infinite Geometric Sum

s(Infinity) = a(1) / 1-r

Circular Permutation (All)

n!/n

Circular Permutation (Some)

nPr/r

Key-Ring/ Bracelet Permutation (All)

n!/2n

Key-Ring/ Bracelet Permutation (Some)

nPr/2r

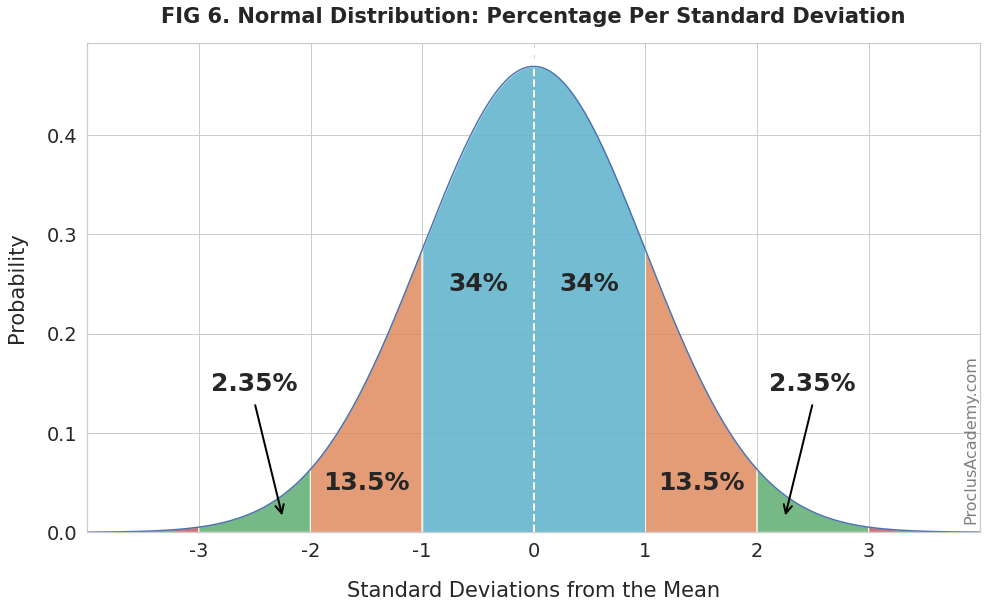
Normal Distribution Graph