College Algebra Final

(x+y)²=

x²+2xy+y² is the ___, which includes the square of each term and twice the product of the two terms.

(x-y)²

x²-2xy+y²

Quadratic Formula

The _____ is a method for solving quadratic equations, given by the expression x = (-b ± √(b²-4ac)) / 2a, where a, b, and c are coefficients of the equation ax² + bx + c = 0.

Zero-Factor Property

If the product of two factors is zero, then at least one of the factors must be zero.

Square Root Property

A property stating that if x² = k, then x = ±√k, allowing the solving of equations by taking the square root of both sides.

Completing The Square

Solve Using the Square Root Property

Difference of Squares

x²-y²=(x+y)(x-y)

Perfect Square Trinomials

x²±2xy+y²=(x±y)²

Difference/Sum of Cubes

x³±y³=(x±y)(x²∓xy+y²)

Product Rule for Exponents

a^m*a^n = a^{m+n}

Quotient Rule for Exponents

a^m/a^n = a^{m-n}

Zero Exponent

a^0 = 1 for any non-zero number

Negative Exponent

a^{-n} = 1/a^{n}

Power Rules for Exponents

(a^m)^n=a^mn

(ab)^m=a^mb^m

(a/b)^m=a^m/b^m

sum/difference function

(f±g)(x)=f(x)±g(x)

Product Rule for Radicals

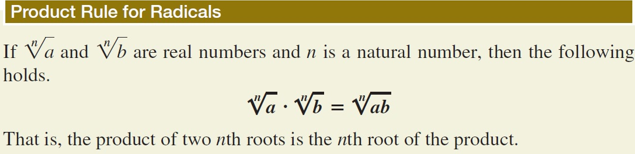
Quotient Rule for radicals

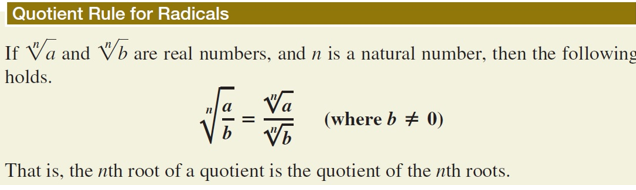
Distance Formula

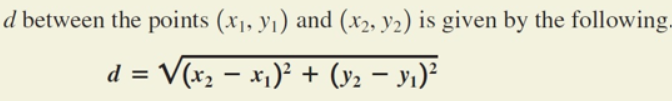
Equation of a Circle (Center-Radius Form)

An equation that represents a circle in the Cartesian plane, defined by the form ((x-h)^2 + (y-k)^2 = r^2), where ((h,k)) is the center and (r) is the radius.

Discriminant

In a quadratic equation ax² + bx + c = 0, the ____, given by b² - 4ac, determines the nature of the roots. If positive, there are two distinct real roots; if zero, one real root; if negative, two complex roots.

Logarithm

y=log^ax = x=a^y

Midpoint Formula

The ____ is used to find the midpoint of a line segment given two endpoints, calculated as ((x1 + x2)/2, (y1 + y2)/2).

Slope-intercept form

y=mx+b

Point-slope form

y-y1=m(x-x1)

Slope Formula

m = (y2 - y1) / (x2 - x1)

Product Rule for Logarithms

Logarithm of a product equals the sum of the logarithms: logb(xy) = logb(x) + log_b(y)

Quotient Rule for Logarithms

Logarithm of a quotient equals the difference of the logarithms: logb(x/y) = logb(x) - log*b(y)

Power Rule for Logarithms

Special Factoring Rules

x²-y²=(x+y)(x-y)

x²±2xy+y²=(x±y²)

x³±y³=(x±y)(x²±xy+y²)

Difference of Squares

x²-y²=(x+y)(x-y)