FTCE - K-6 - Math

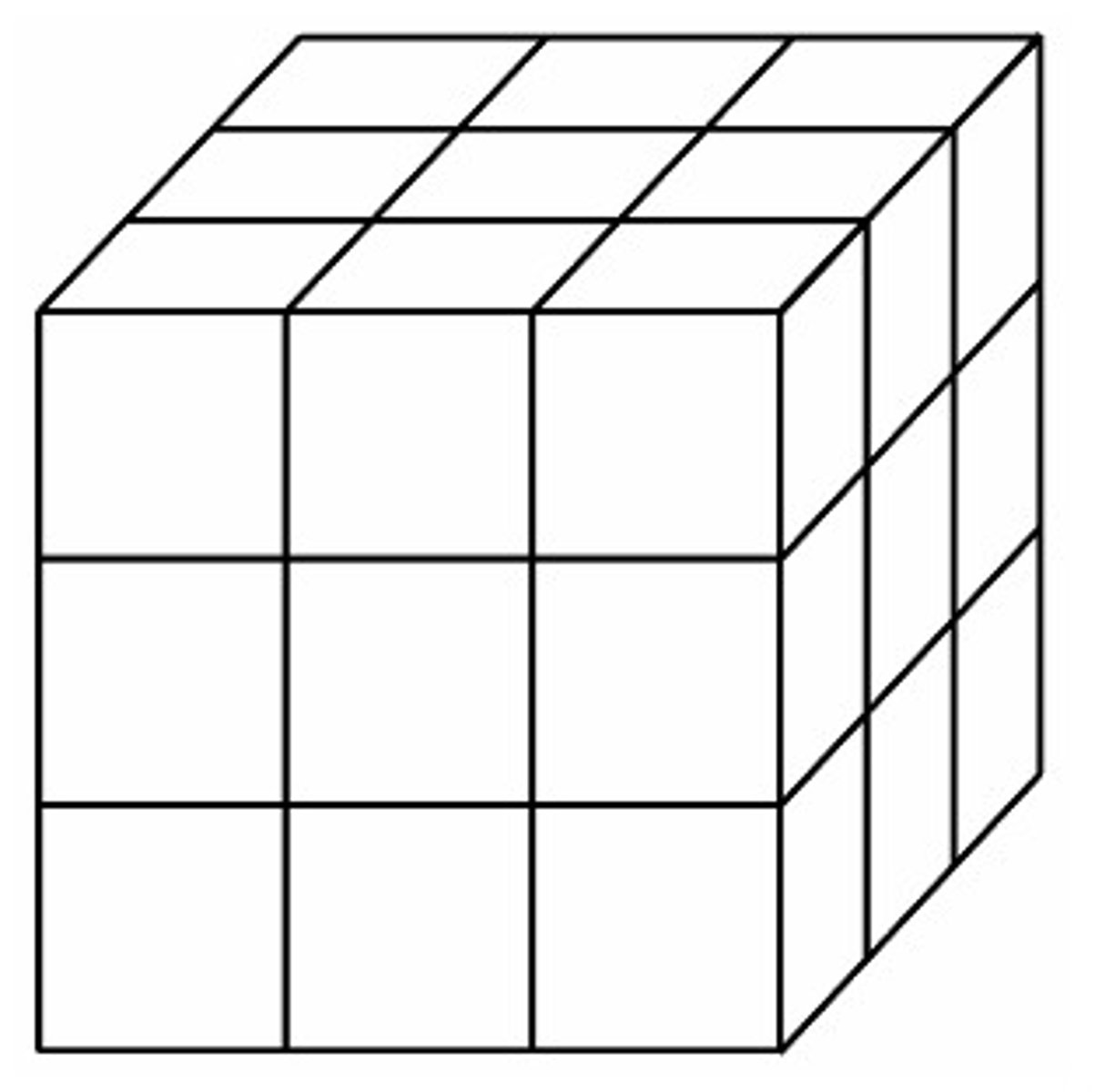
Volume

The amount of space an object takes up. Always cubed. Ex, cm3, m3, ft3, mi3

Area

Length x Width, always squared. Ex, cm2, m2, ft2, mi2

Distance

The length of a path between two points. Ex, cm, m, ft, mi.

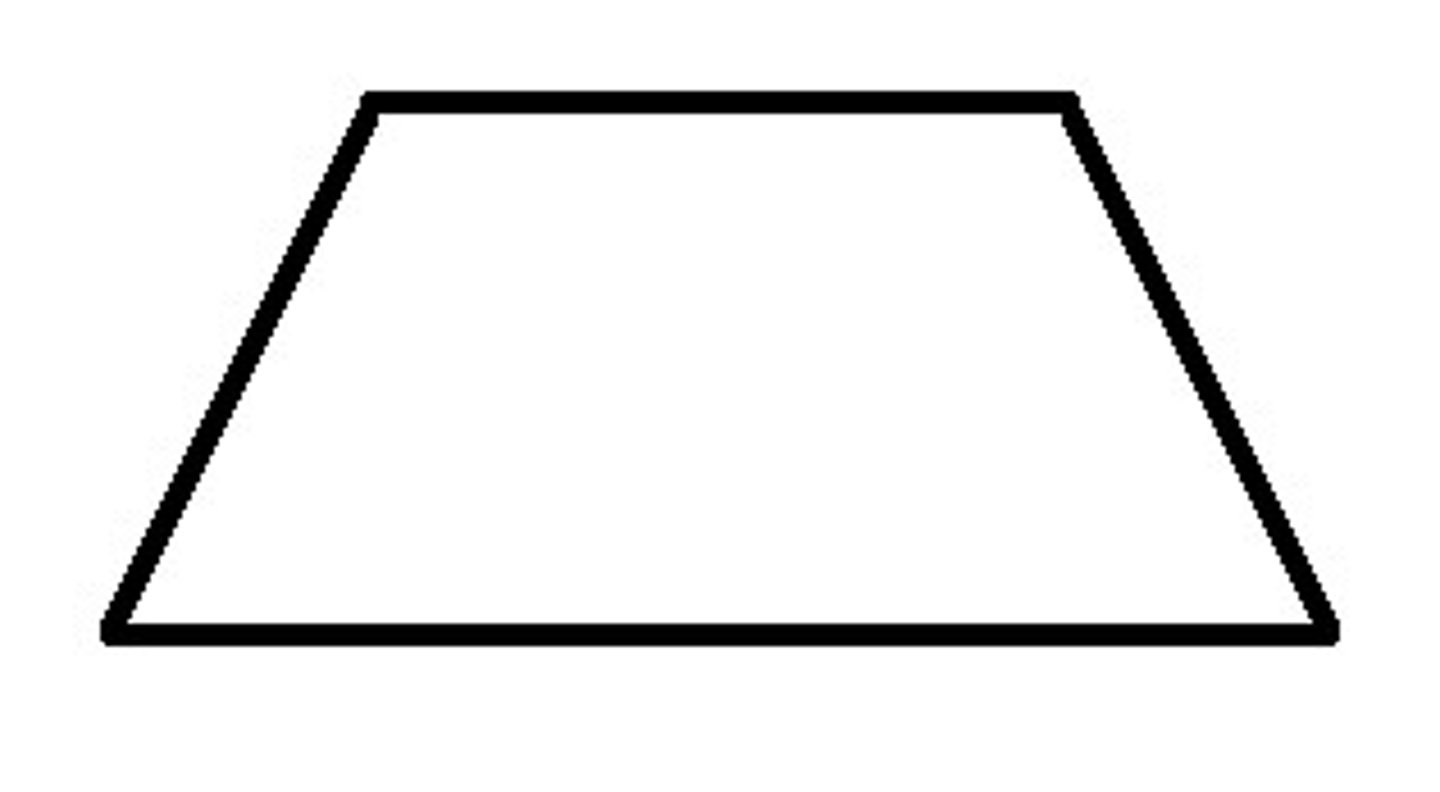
Trapezoid

A=1/2h(b1+b2)

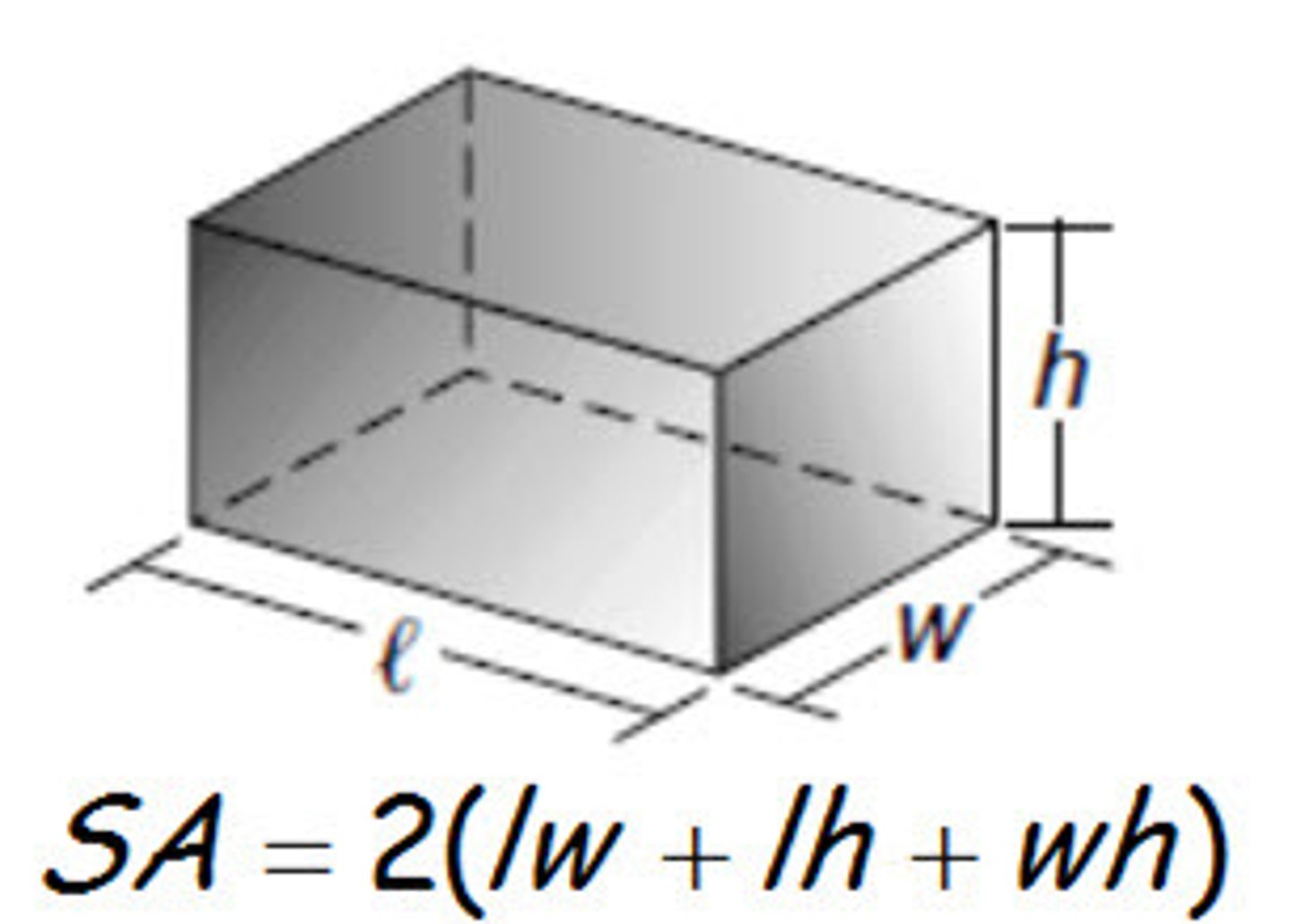
Surface Area of Rectangular Prism

2(ac+ab+bc)

Triangle

A=1/2bh

2D shape

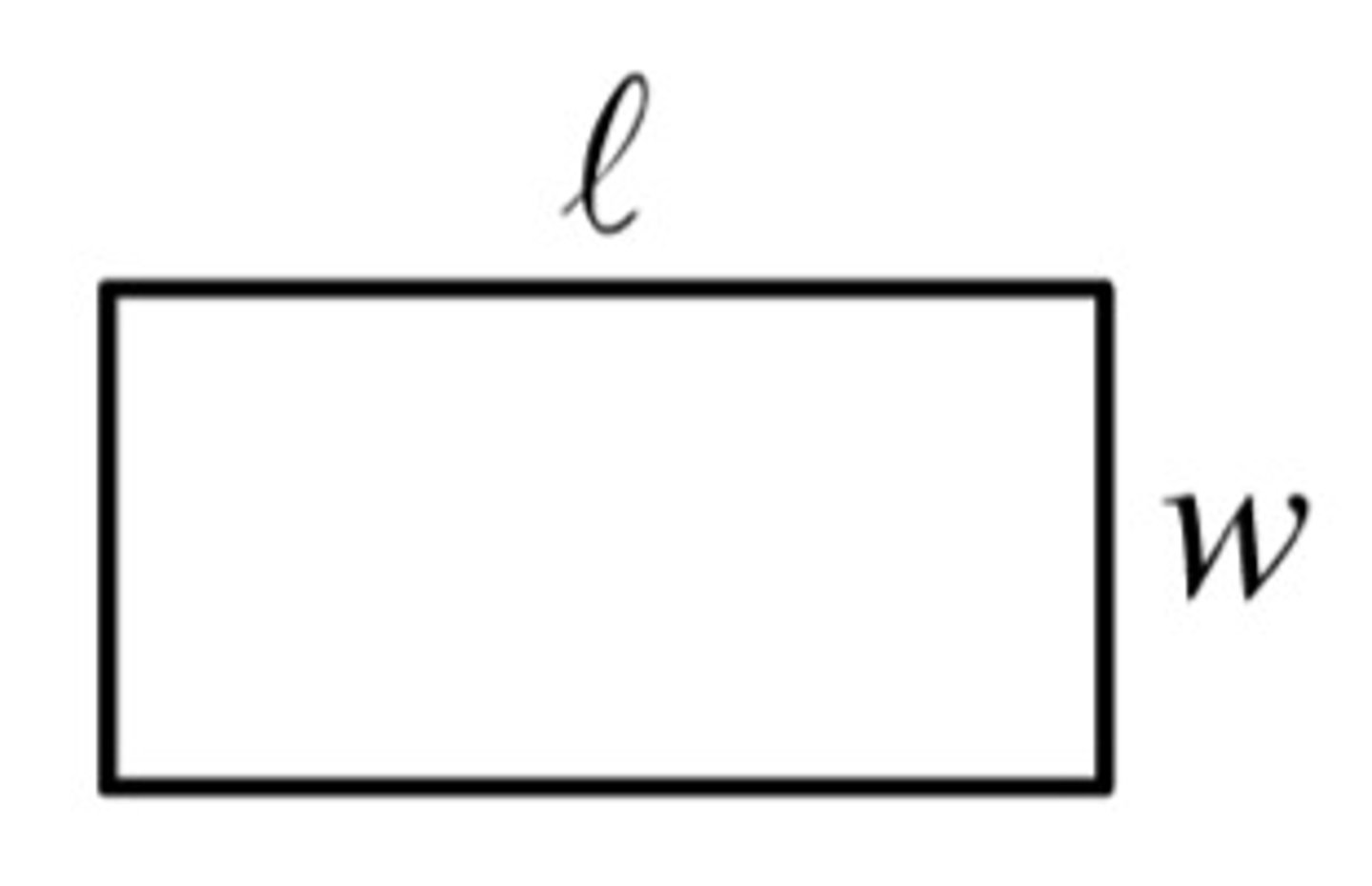
Rectangle

A=LxW

Quadrilaterals

All the angles are 90 degrees, right angle.

Distributive Property

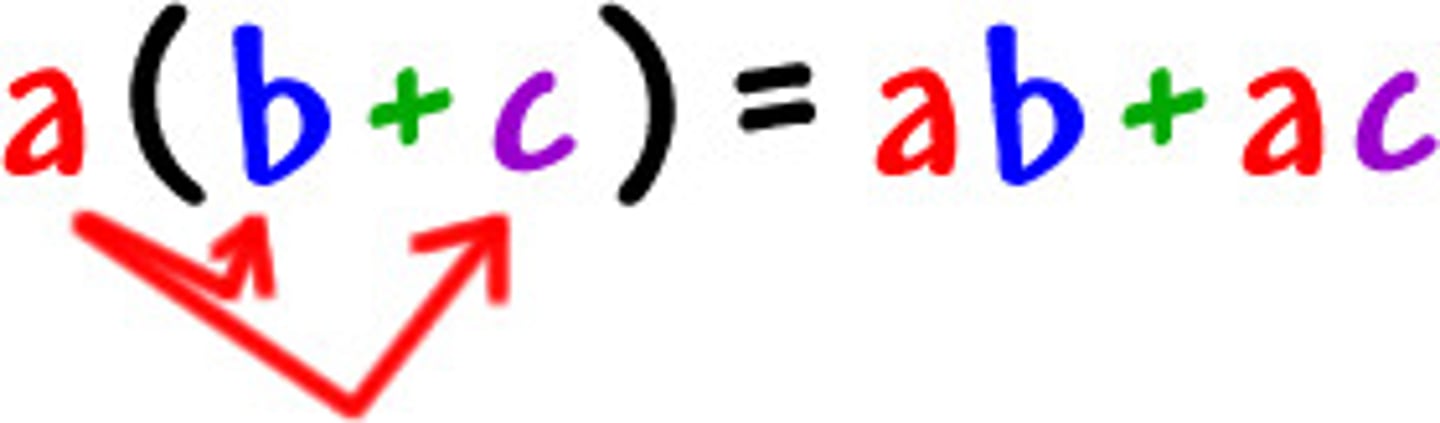
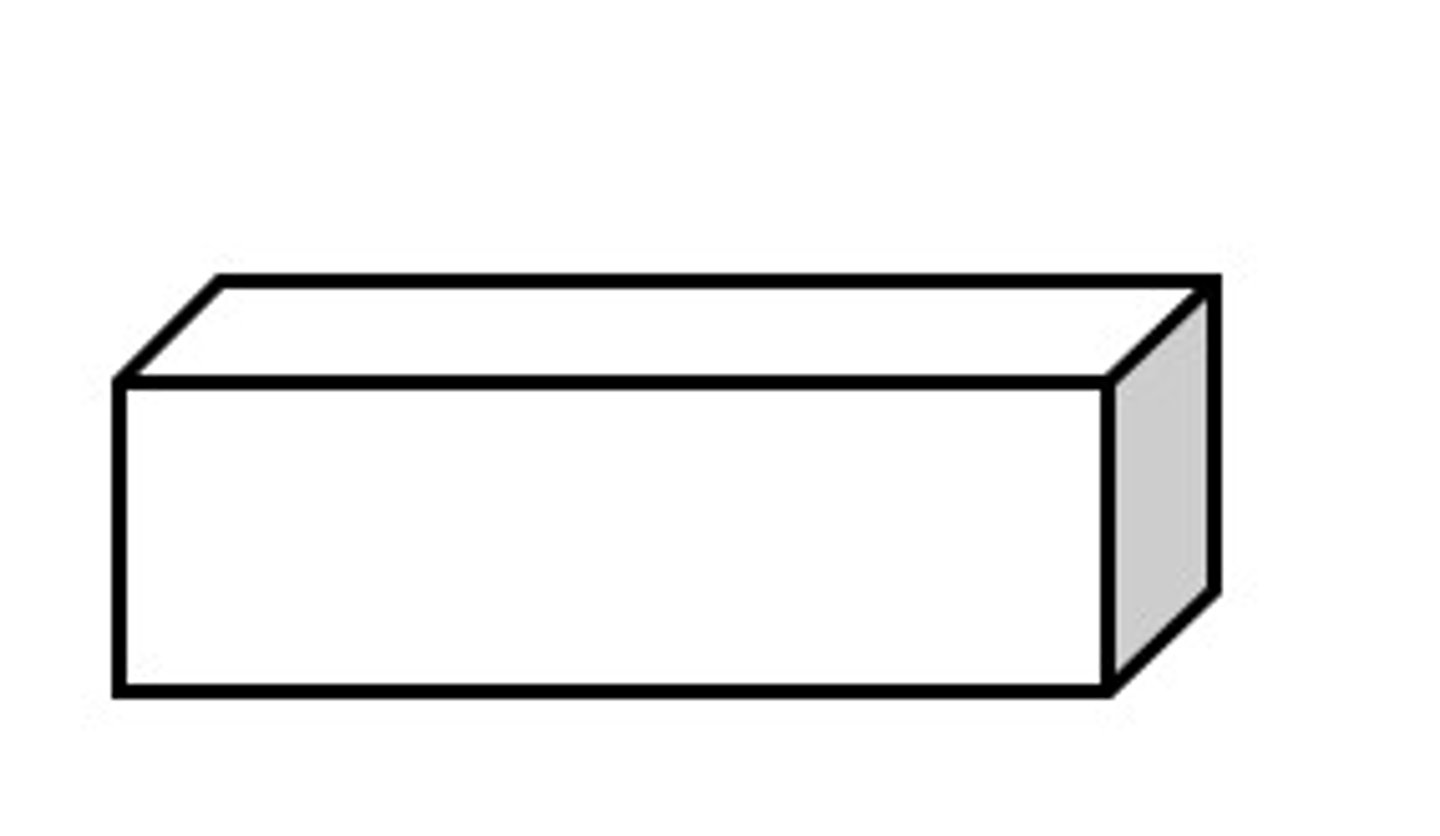
Rectangular Prism

The polyhedron that has the most vertices.

Add To, Change Unknown

11+____=22

Nets

When you unfold a 3 dimensional shape to observe it as a 2 dimensional shape.

Heptagon

Has 7 sides.

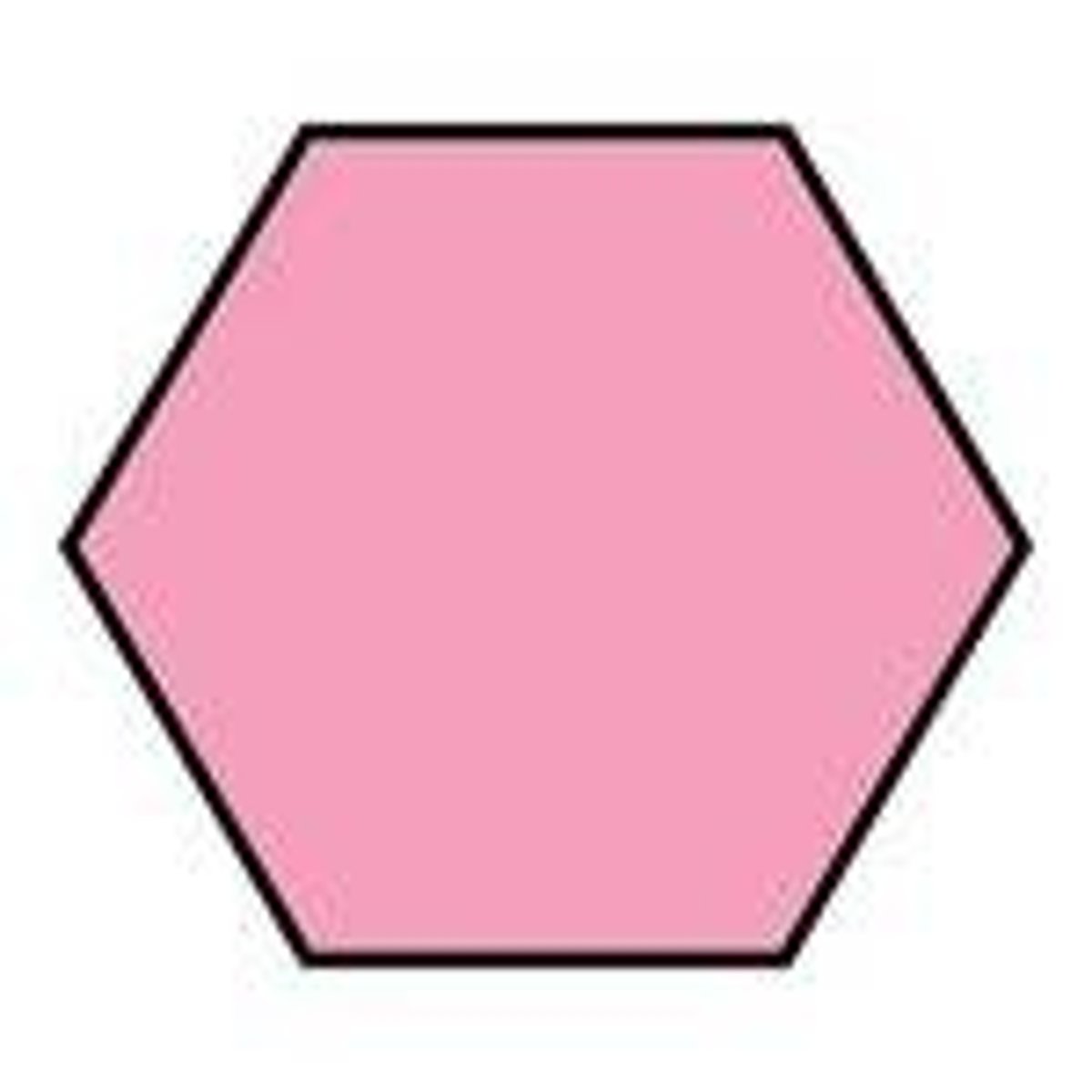
Hexagon

Has 6 sides.

Circumference

The distance around a circle

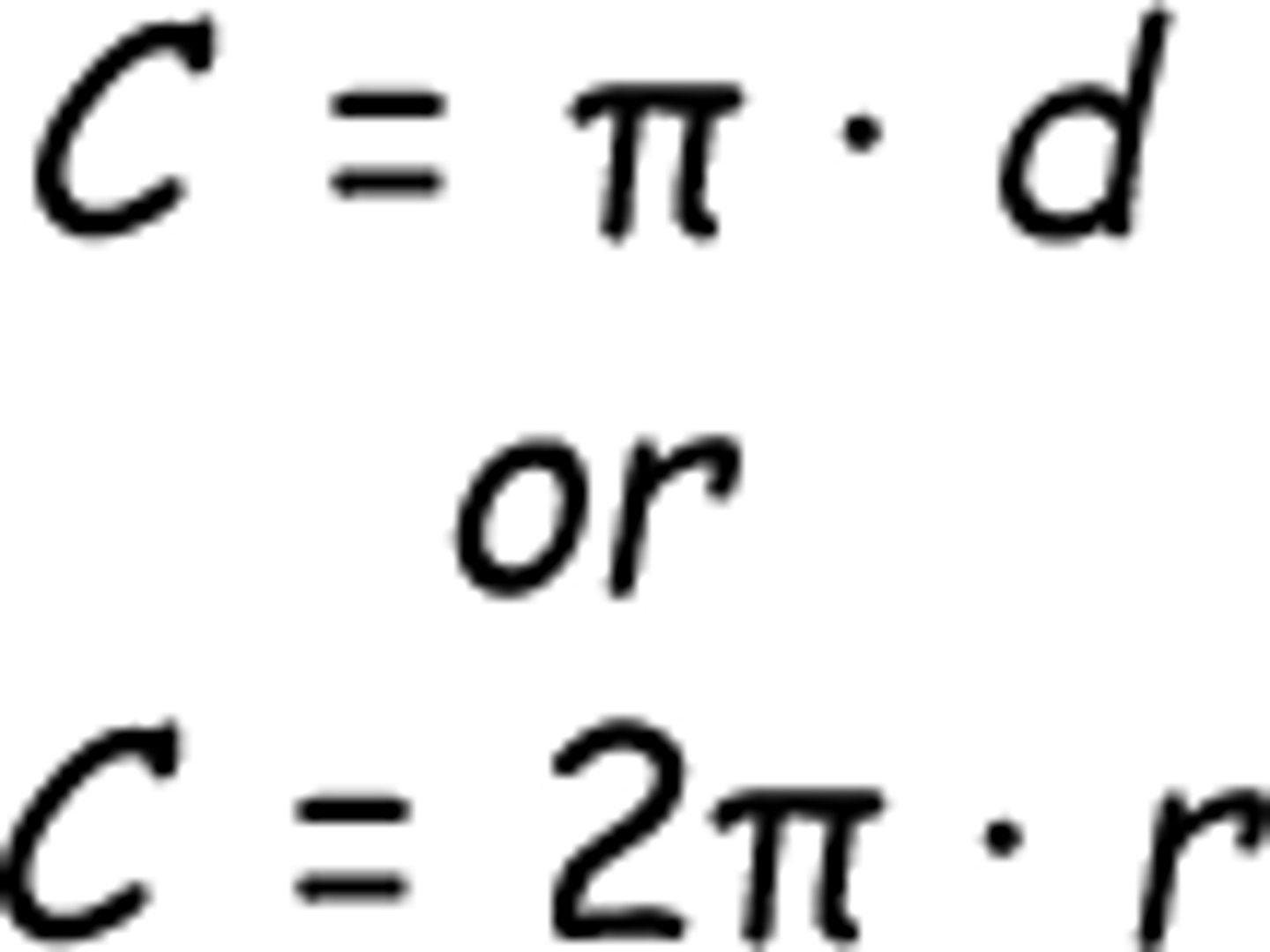
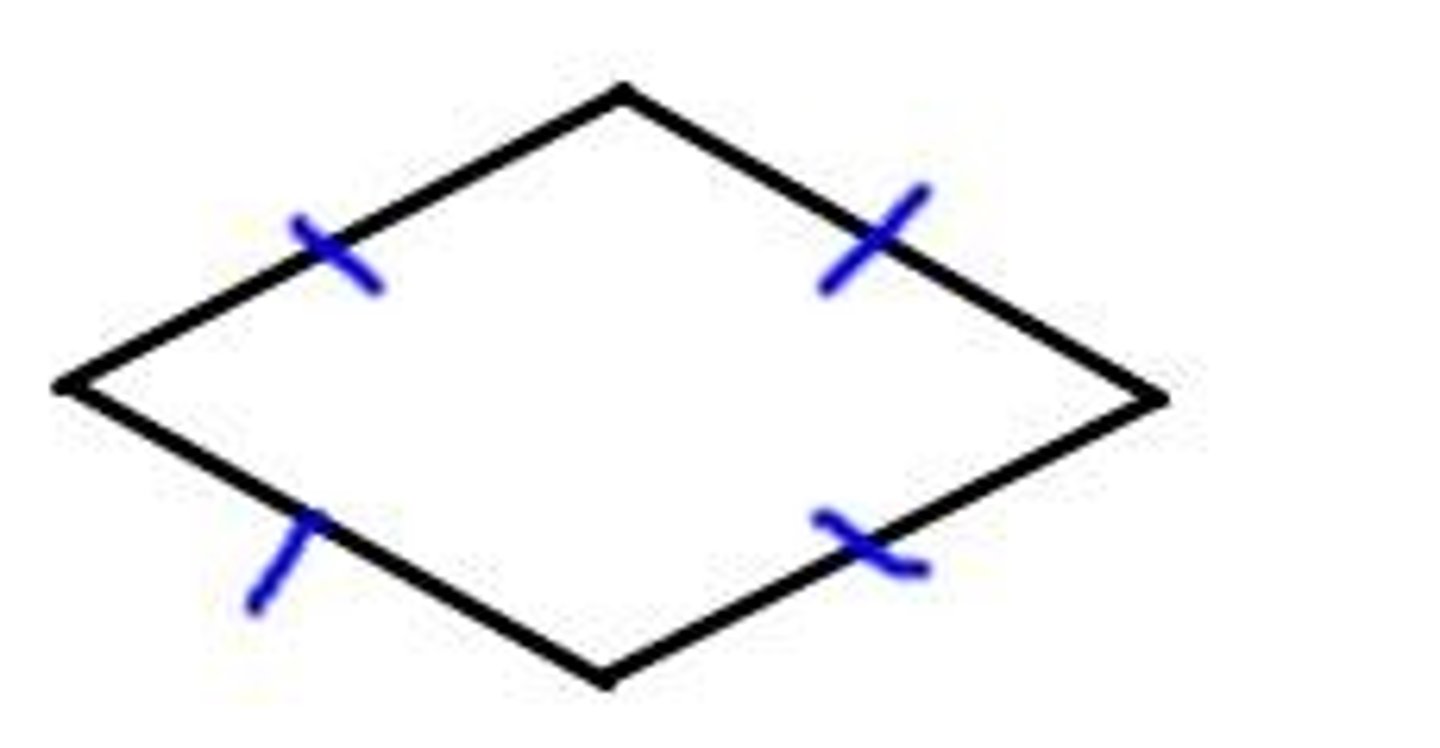
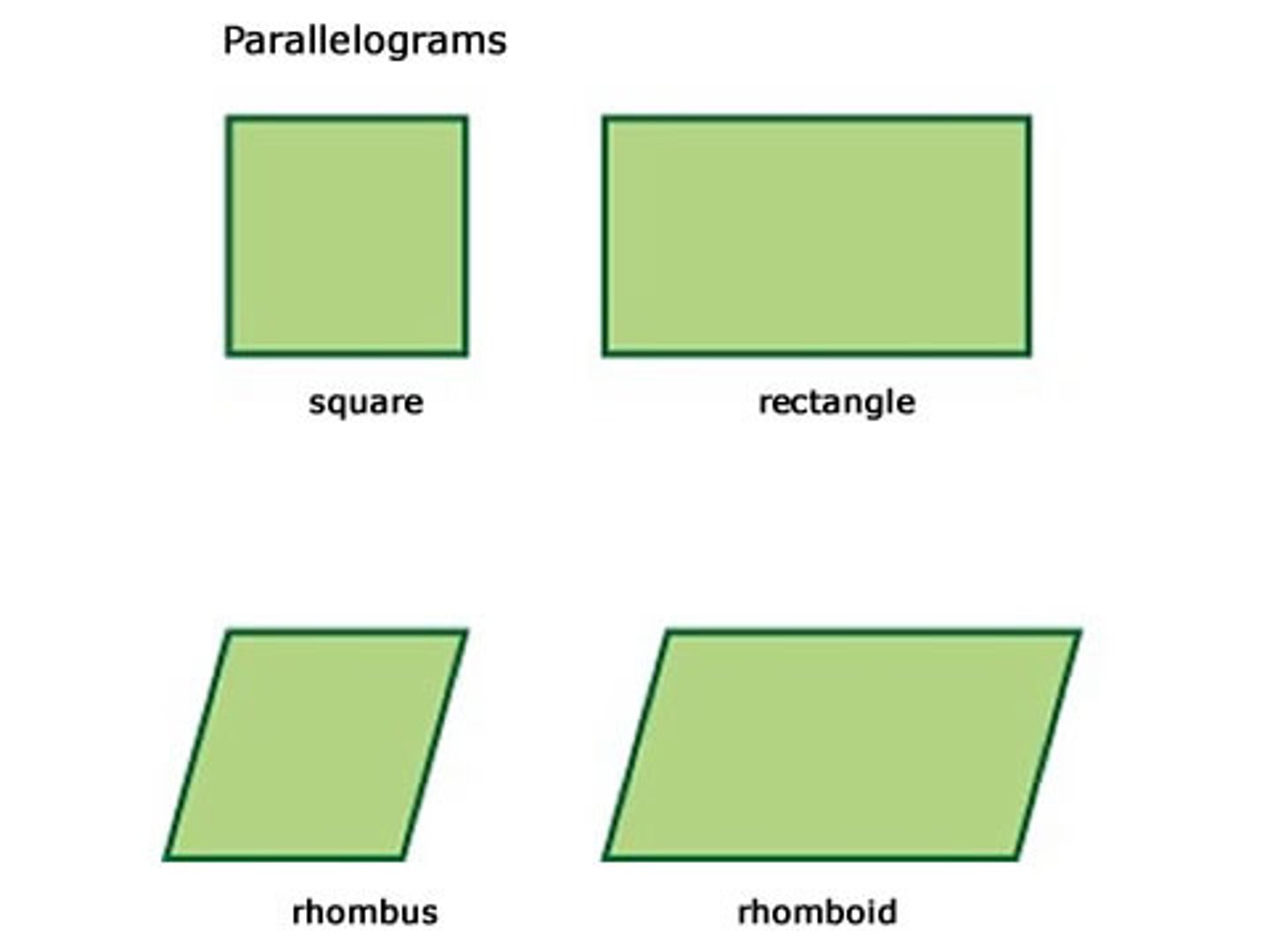
Rhombus

A parallelogram with four congruent sides

Circle

a round shape that has no beginning or end

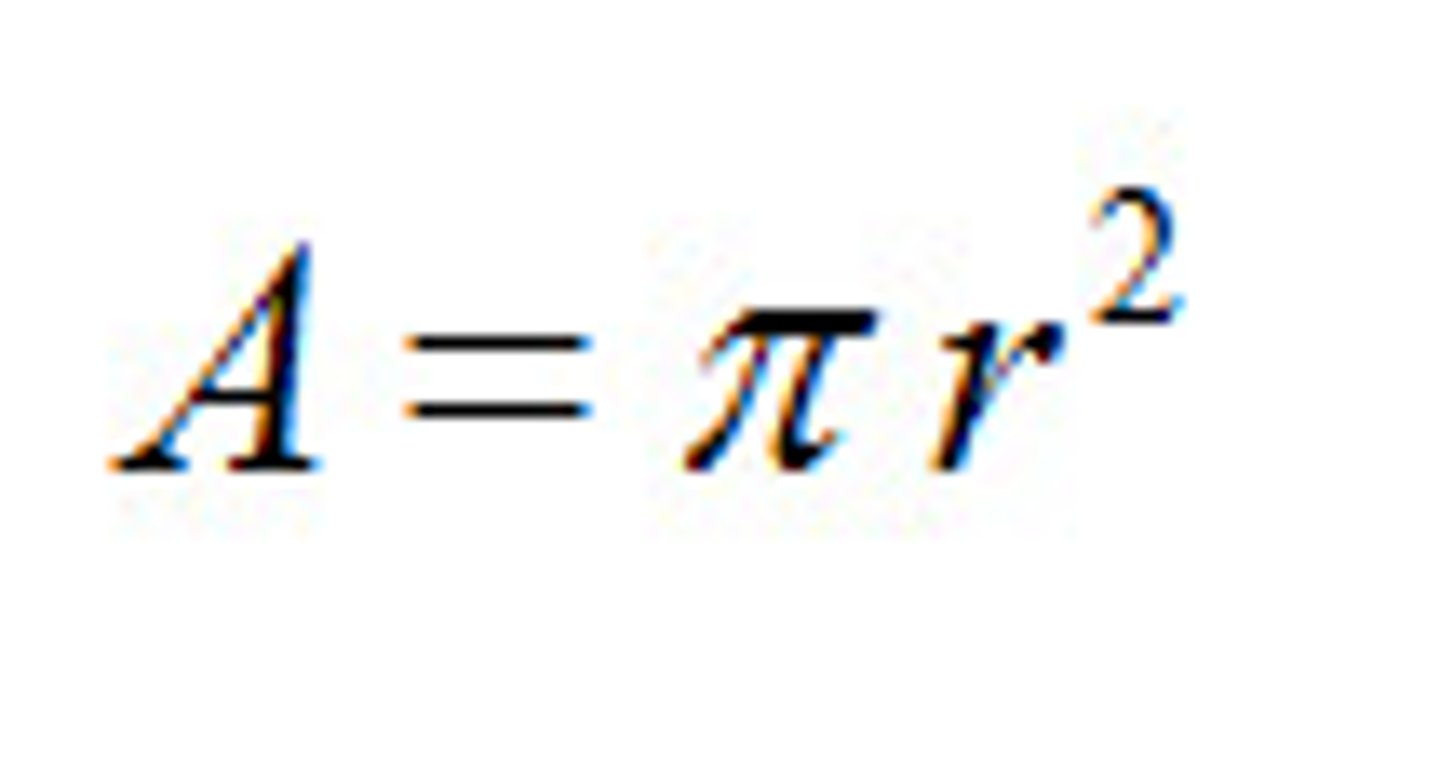
Distributive Multiplication

a(b+c)=ab+ac

Transitivity

After learning that A = B and B = C, the learner demonstrates that A = C without direct training on that relationship. a>b

PEMDAS "Order of Operations"

Parenthesis

Exponents

Multiply/Divide

Add/Sub

Addition Property of Equality

If a = b, then a + c = b + c

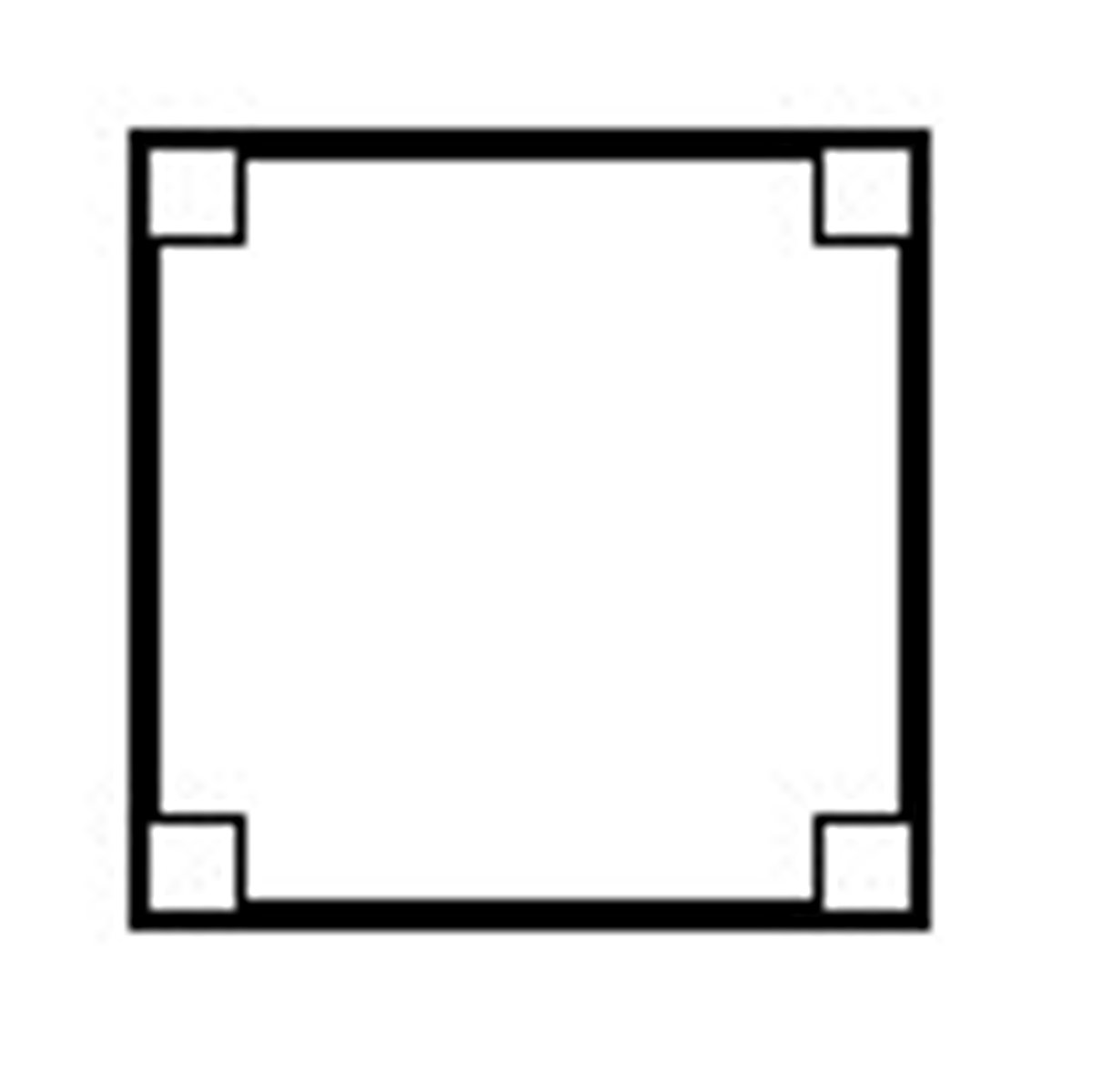
Square

A parallelogram with four congruent sides and four right angles.

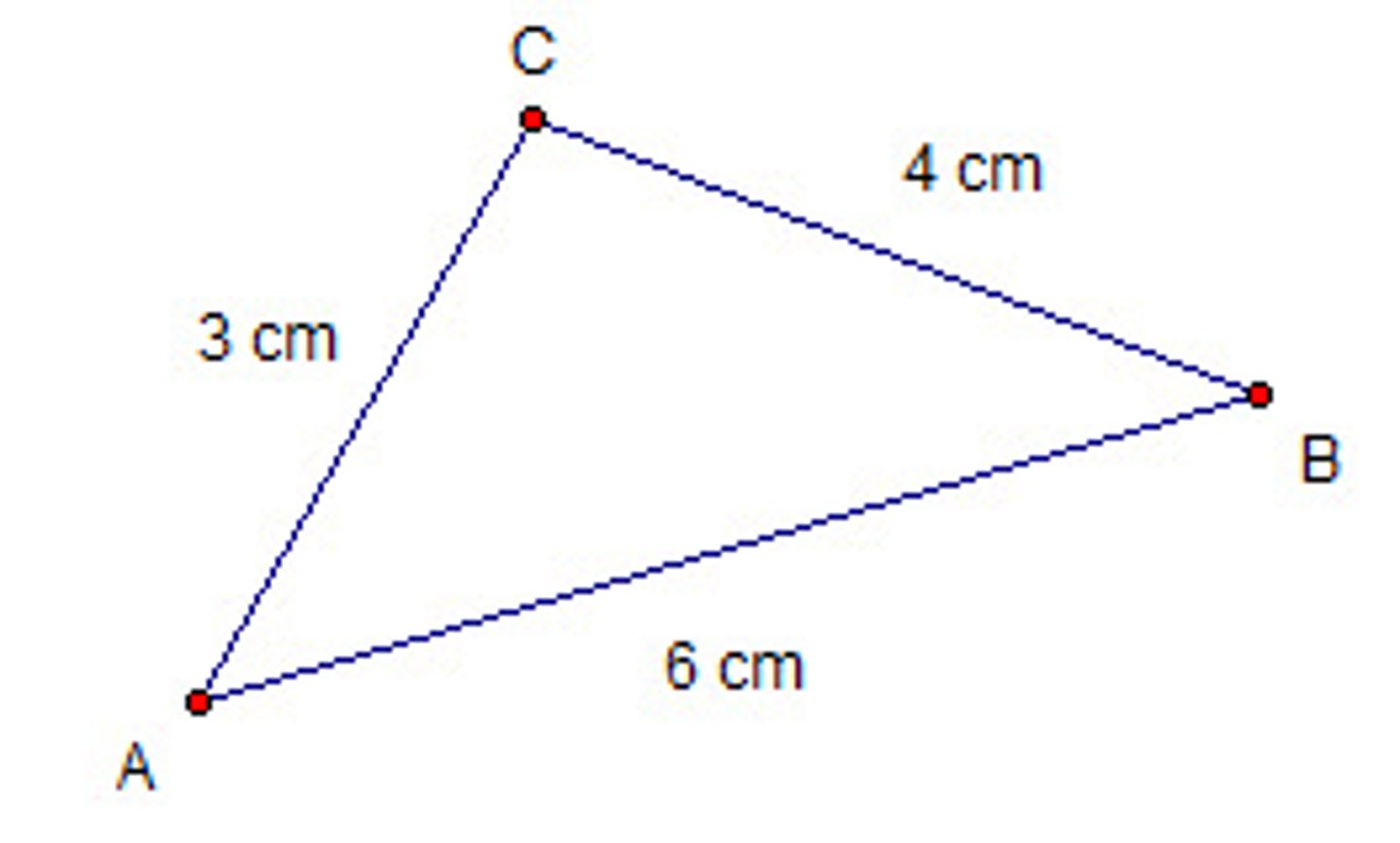
scalene triangle

a triangle with no congruent sides/equal sides.

Compensation

Borrowing pieces of one number to compensate for another to make it easier to solve.

46+38

Take 4 from 38 and give it to 46.

50+34=84

Turn number into the tens spot.

Multiples

What we get AFTER multiplying the number by an integer (not a fraction.) 0x6=0

0 is a multiple of 6. 1x6=6 so 6 is a multiple of 6

Polygon

A closed figure formed by three or more line segments. A closed figure starts and ends at the same point.

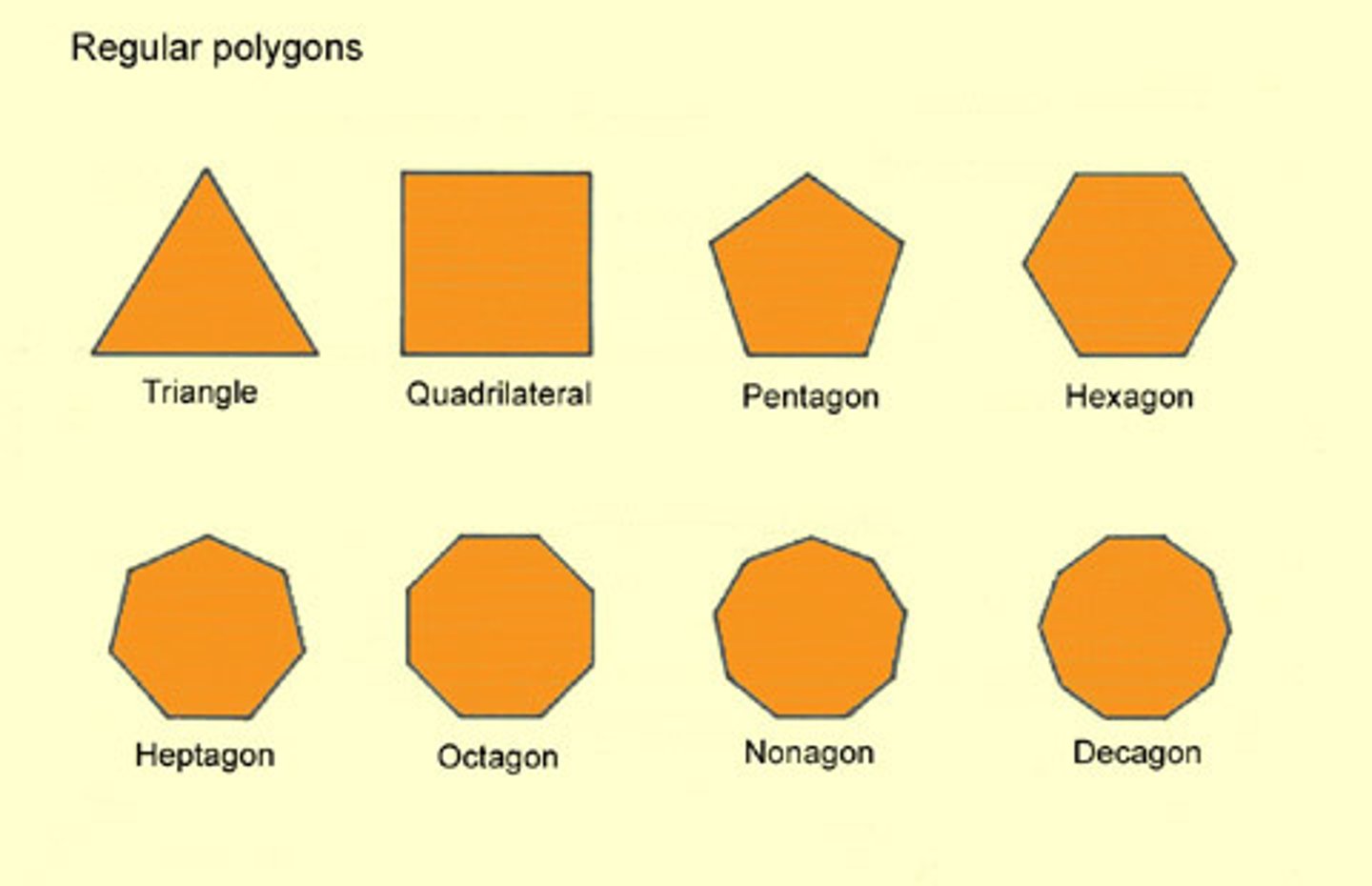
Pentagon

A 5-sided polygon (a flat shape with straight sides).

Octagon

a polygon with 8 sides and 8 angles

Euler's Theorem

F+V=E+2

(Faces)+(Vertices)=(Edges)+2

Negative Exponents

3^(-1)=1/3 To make a negative exponent positive: Move the power between the numerator and denominator.

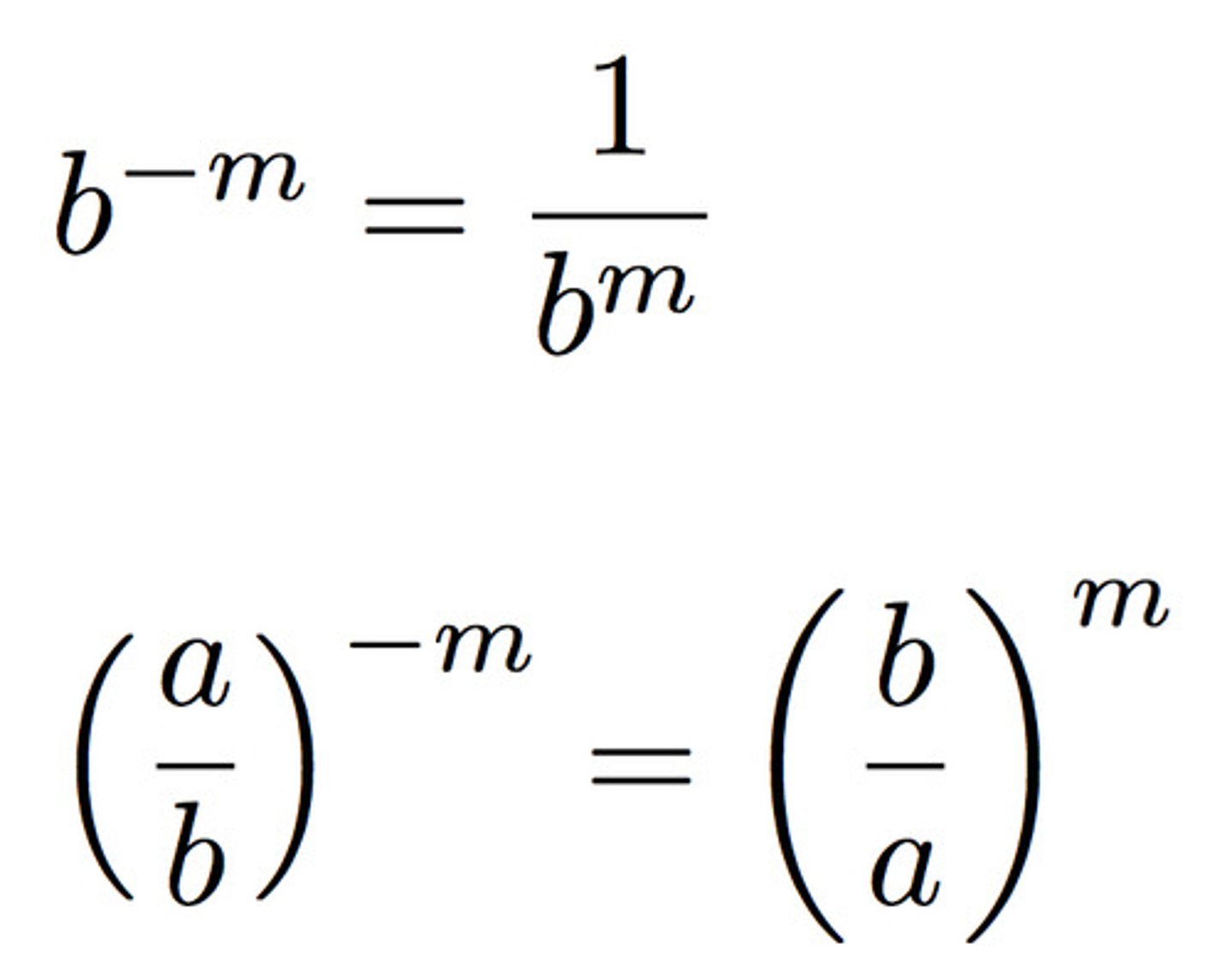
Iteration

Repeating the same steps over and over again. Anything that is sequential in operation is iteration. Ex, using a paperclip one after another to measure the length of a desk. Following the steps for the standard algorithm in addition.

Pythagorean Theorem

a²+b²=c²

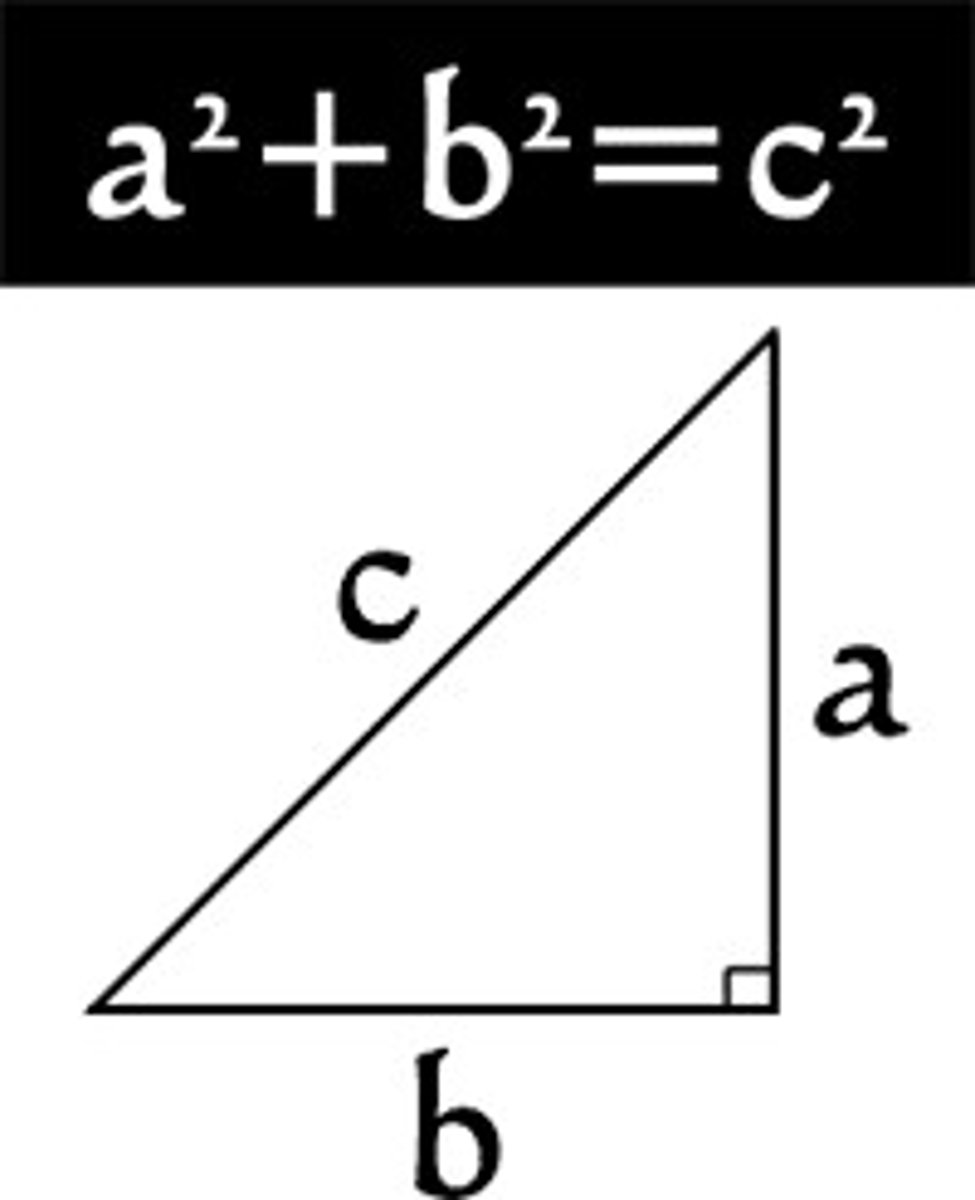
Acute Triangle

A triangle that contains only angles that are less than 90 degrees.

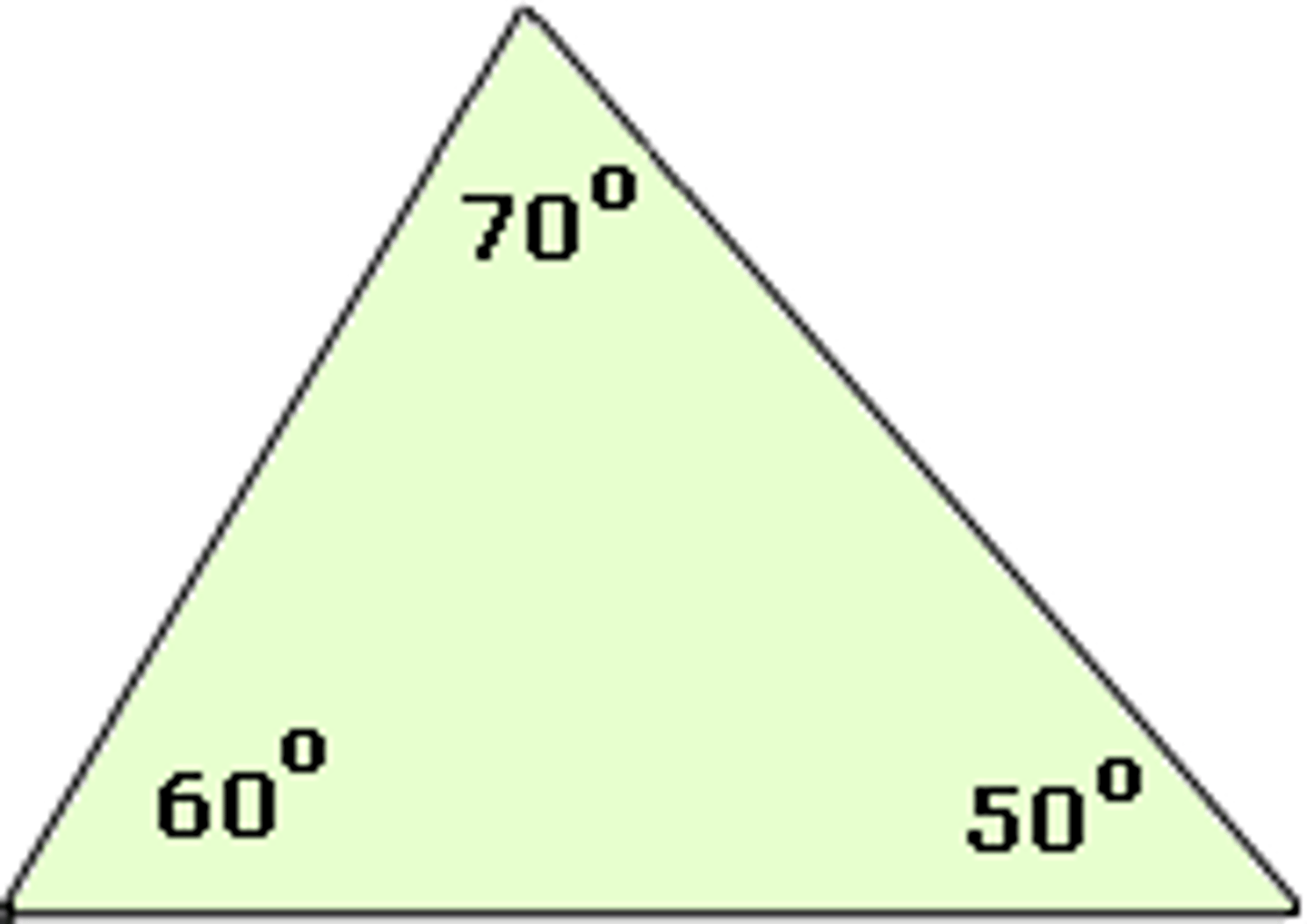
Obtuse Triangle

A triangle with one angle that is greater than 90 degrees.

Parity

the state or condition of being equal, especially regarding status or pay. The fact being even or odd.

inventive strategies

Methods in which students invent ways to solve complex problems. They involve using reason and understanding to get to the end result.

Diagnostic Assessment

a form of assessment designed to provide teachers with information about students' prior knowledge and misconceptions before beginning a learning activity

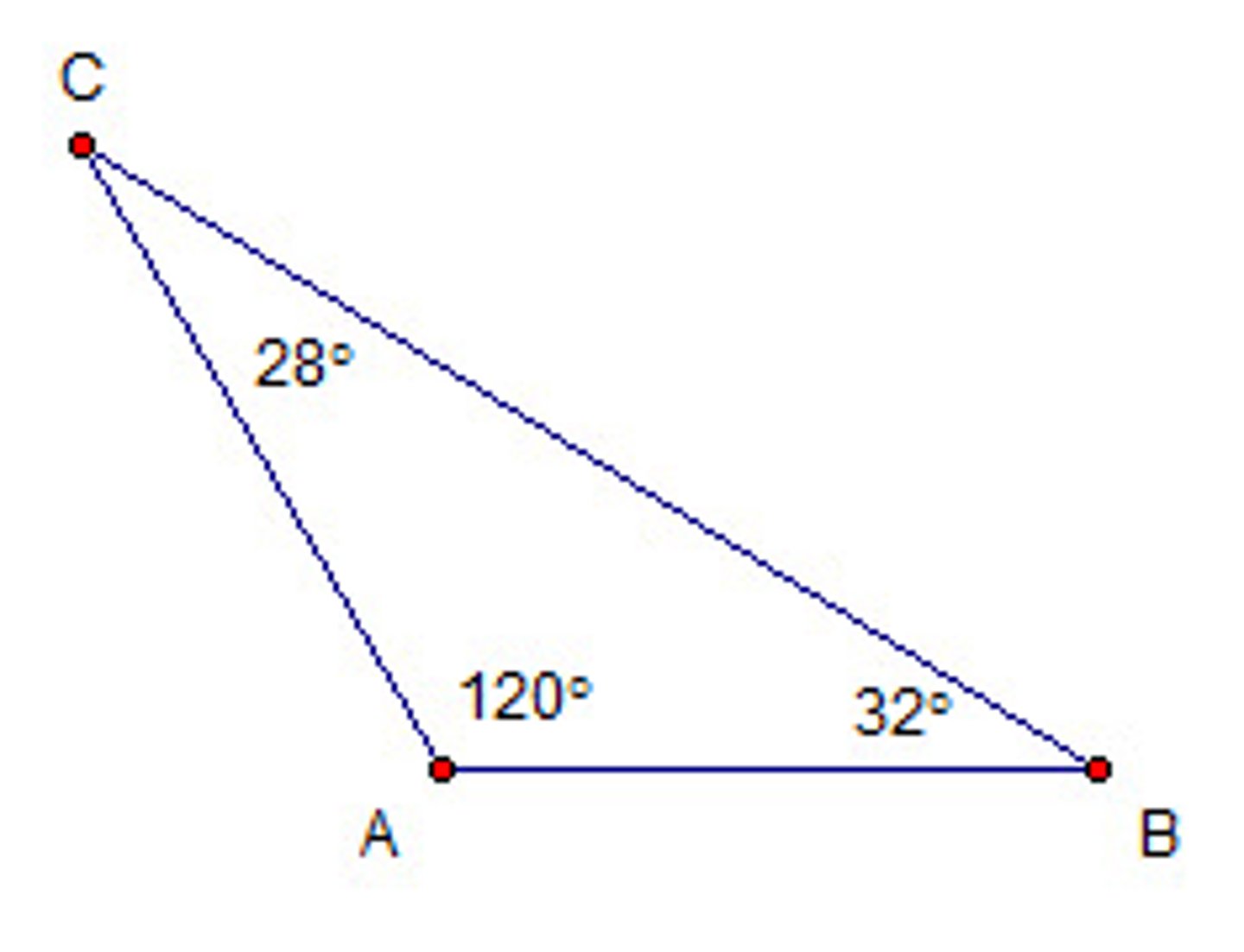
Right Triangle

A triangle that has a 90 degree angle.

Criterion-Referenced Assessment

an assessment procedure in which a student's performance is compared to a particular level of mastery. FCAT, FSA, EOC

Subtraction Property of Equality

a=b then a-c=b-c

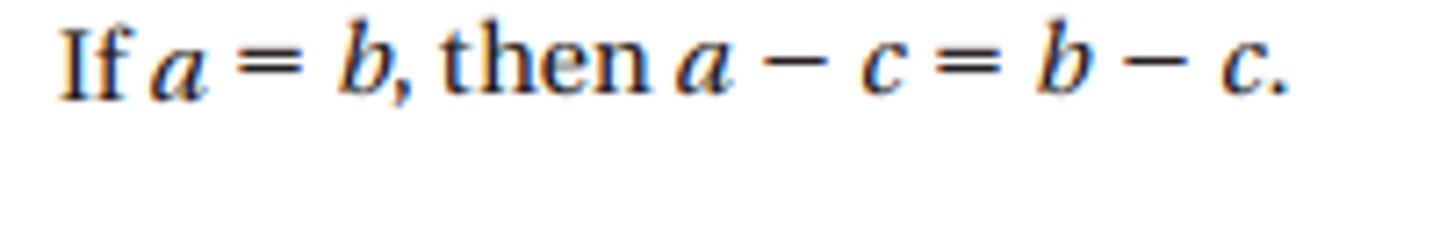
Division Property of Equality

a=b

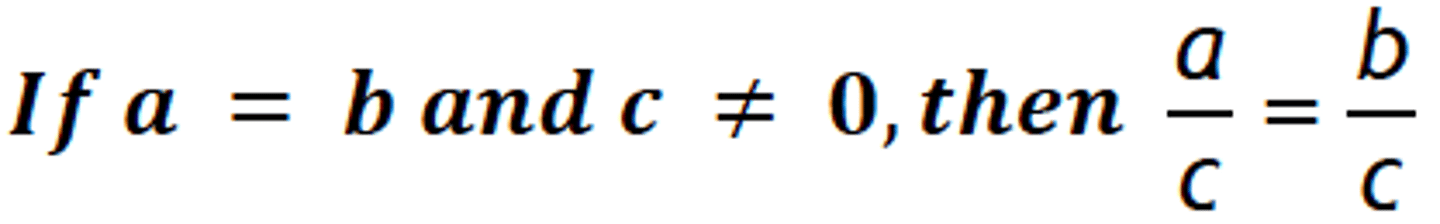
Take From, Start Unknown

Rachel had some CDs. After she gave 23 away, she had 18 left. How many CDs did Rachel have before? ?-23=18

Take From: Result Unknown

Rachel had 41 CDs. She gave away 23. How many does she have now? 41-23=?

Add to: Start Unknown

Rachel had some CDs. After she got 18 more, she had 41 CDs. How many CDs did Rachel have before? ?+18=41

Tiling

Can be used as a an array for multiplication. Used to present the abstract or concrete.

Transitive Property of Equality

If a=b and b=c, then a=c

CRA

concrete, representational, abstract

RCP

Reciter (Student counts along with teacher)

Counter (Student counts on their own.)

Producer (Add & Produce Math Problems)

Add to: Change Unknown

2 Bunnies were sitting on the grass. Some more bunnies hopped there. Then there were 5 bunnies. How many bunnies hopped over to the first two. 2+____=5

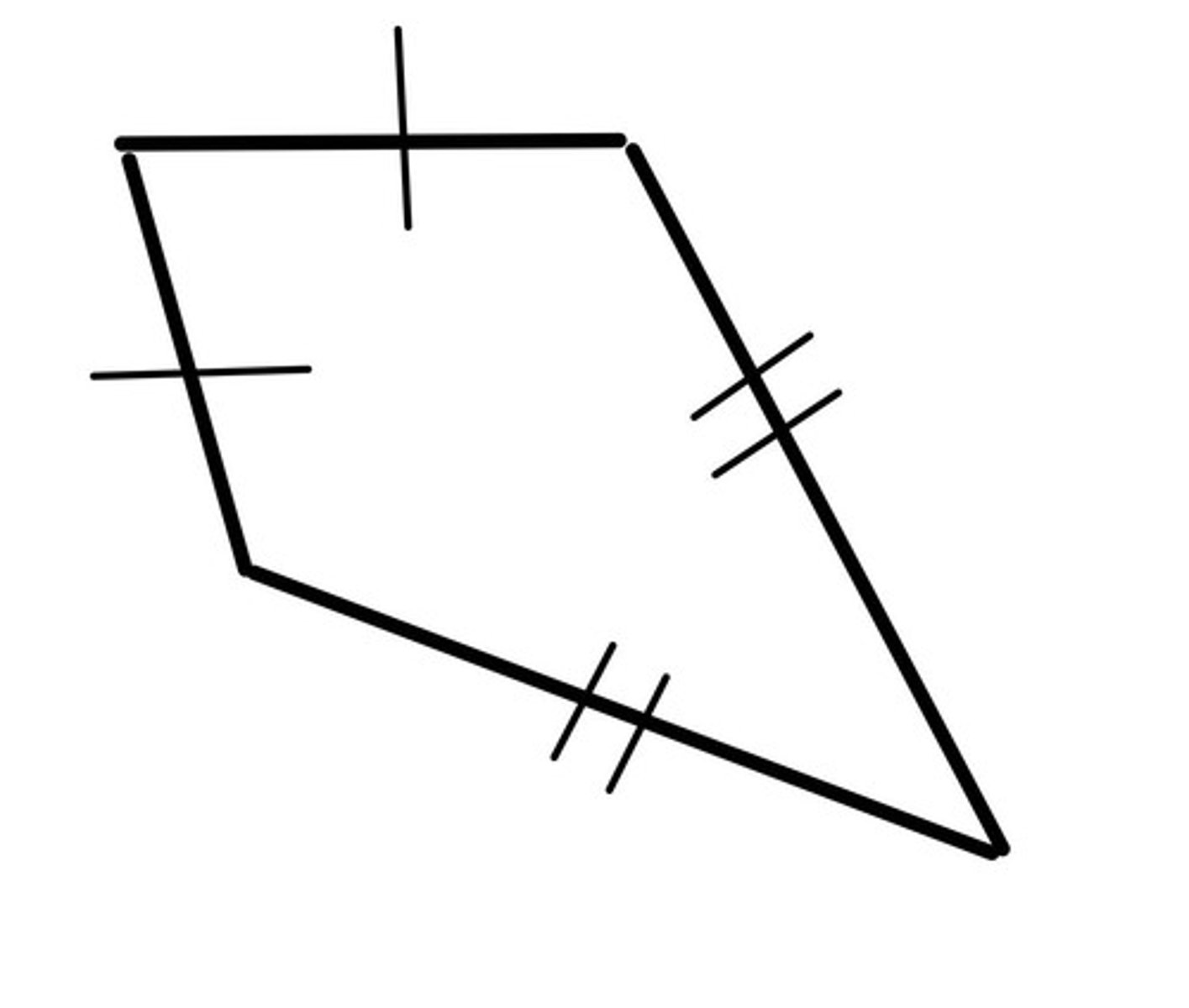
Kite

A quadrilateral that has two pairs of consecutive congruent sides, but opposite sides are not congruent.

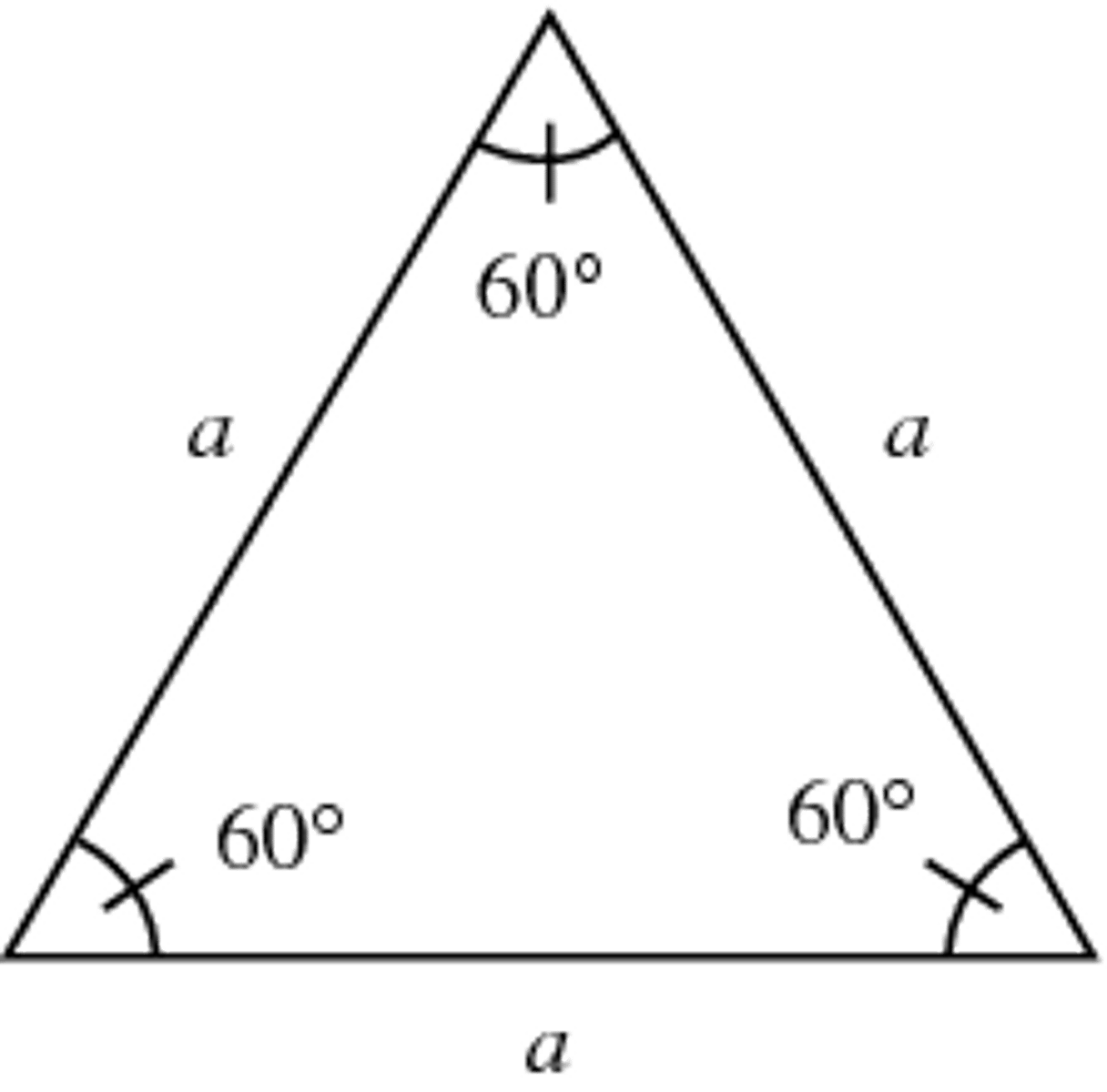
equilateral triangle

A triangle with three congruent sides

Automaticity

the ability to process information with little or no effort

Multiplication Property of Equality

If a=b, then ac=bc

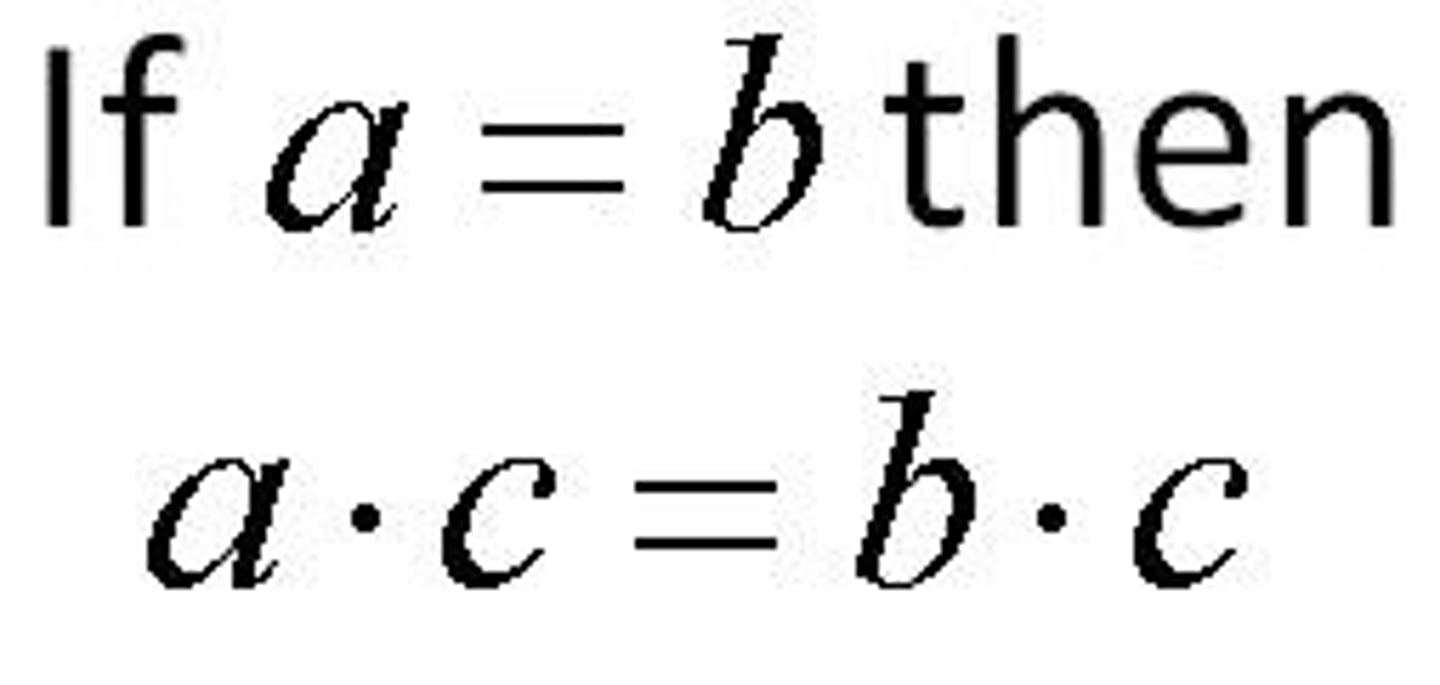
Existence of additive inverses

For every a there exists -a so that a + (-a) = (-a) + a = 0

surface area

2ab+2bc=2ac 2(ab+ac+bc)

put together/take apart addend unknown

Grandma has 5 flowers. How many can she put in the red vase and how many in her blue vase?

_____+_____=5

Parallelogram

opposite sides are equal and parallel. Opposite angles are equal. Quadrilateral=4 sides.

prime number

A whole number greater than 1 that has exactly two factors (1 and itself)

Mode

The value that occurs most frequently in a given data set.

Median

Middle number

Mean

average

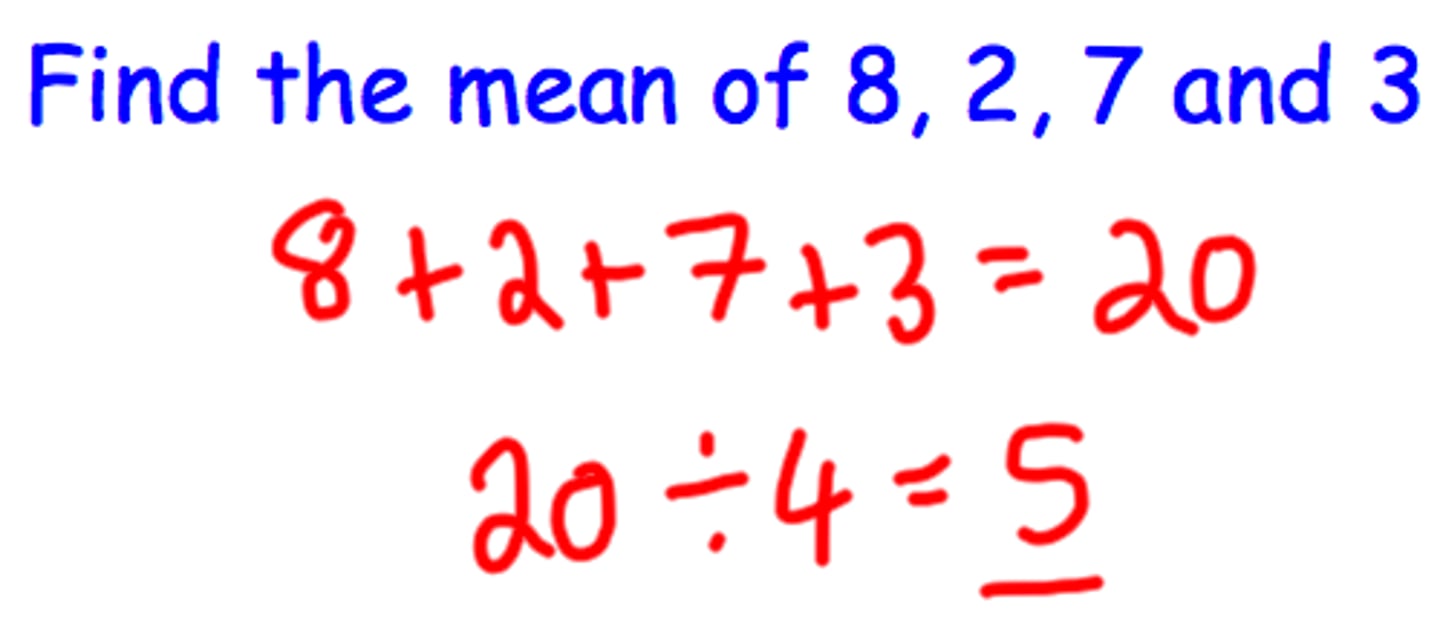
standard algorithm

a step-by-step method for computing, which is used by all teachers and students in the United Ex, regrouping, exchanging, long division, long multiplication, average, area, volume.

Factors

Numbers that are multiplied together to get a product

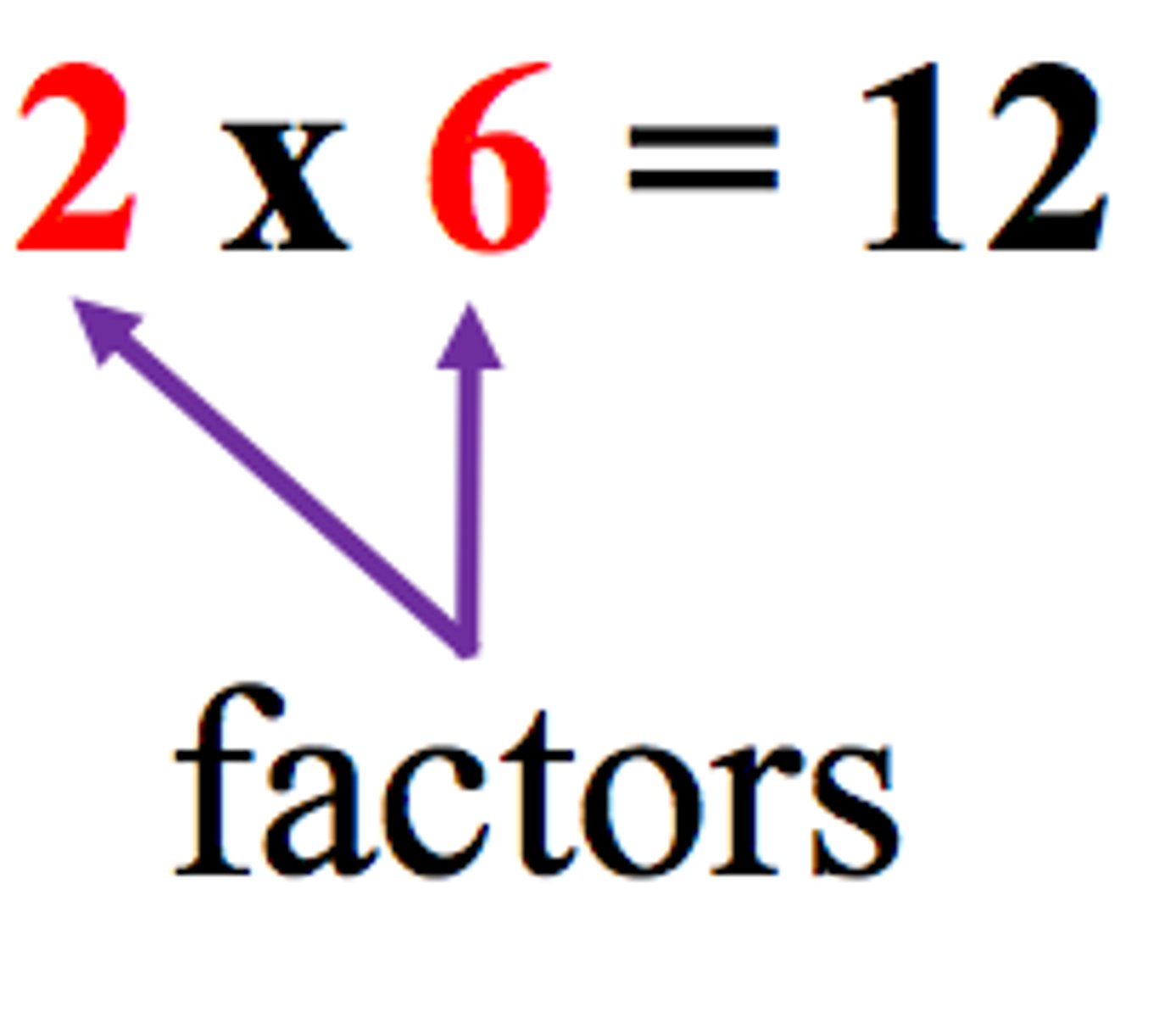
Composites

a number which has more than two factors.

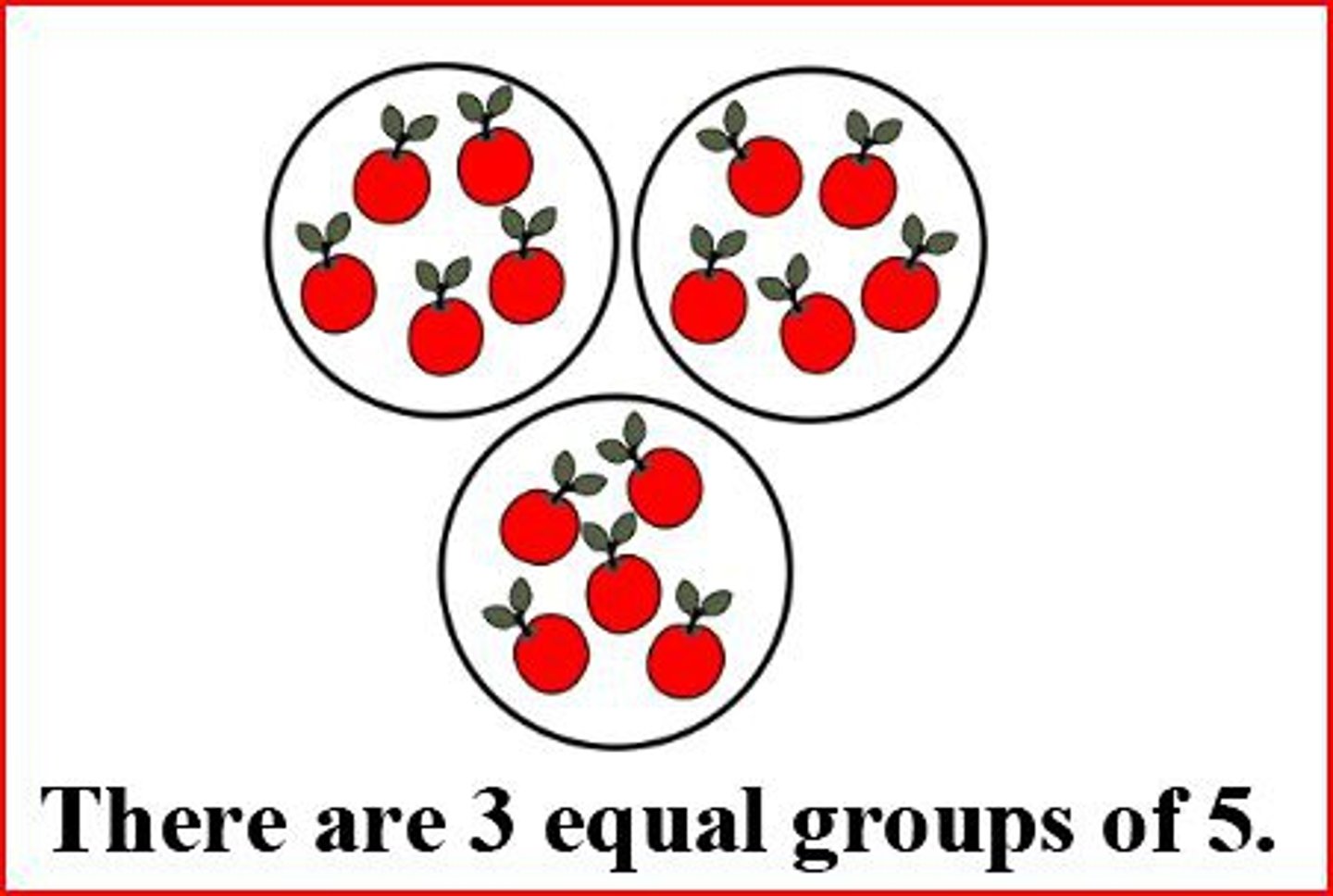
Equal Groups

groups with the same number of objects

Associative Property of Addition

(a+b)+c=a+(b+c)

compacting

Groups of students who can skip steps and move quickly because they have advanced math fluency

norm-referenced assessment

A test that compares student's skills with peers of same grade level, thereby helping ascertain whether a student has acquired the skills needed to function successfully at his or her grade level. Example: Assessment given to determine a need for academic support.

speed

distance/time

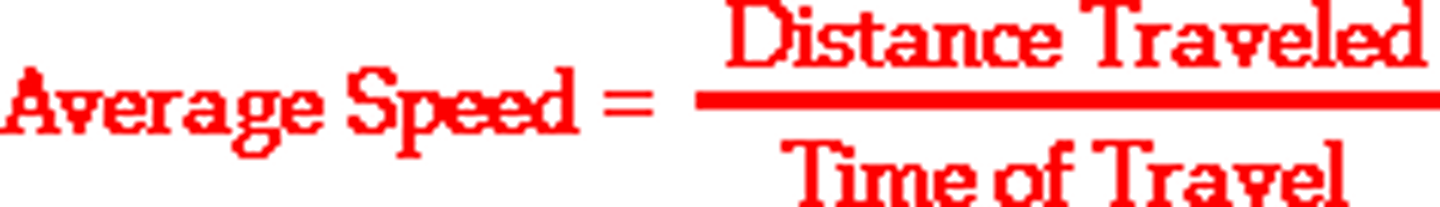
multiplicative identity property of 1

ax1=1xa=a

Rate

How fast the student can solve a problem.

Levels of Geometric thinking

descriptive

analytic

abstract (last)

flexibility

student can solve the problem in different ways

subitize

The ability to look at a number pattern and instantly recognize the quantity in the arrangement without counting.

Add to: Result Unknown

two bunnies sat on the grass 3 more hopped there. How many are on the grass? 2+3=?

Put Together/Take Apart, Total Unknown

3 red apples and 2 green apples are on the table. How many apples are on the table?

3+2=?

Multiplication Comparison

compares by asking or telling how many times as many one number is than another

Ex, The giraffe is 18ft tall. She is 3 TIMES as tall as the kangaroo. How tall is the kangaroo?

Partitioning

Taking large numbers and splitting them into small, manageable units

ex, 467-122

400-100=300

60-20=40

6-2-4

=345

Isosceles Triangle

a triangle with at least two congruent sides

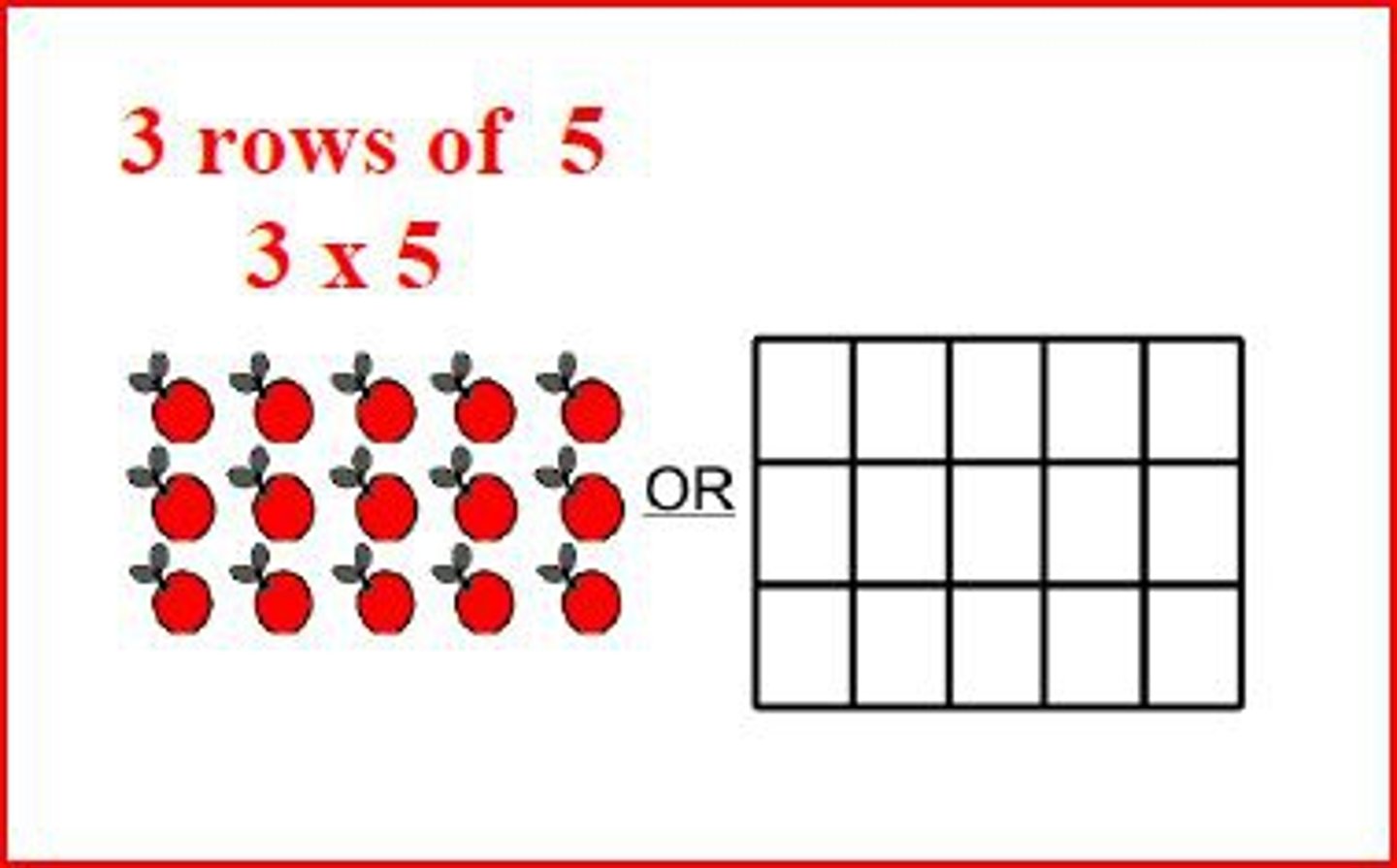
Arrays

a pictorial representation of a multiplication problem

distributive property of multiplication over addition

ax(b+c)=axb+axc

additive identity property of 0

a + 0 = 0 + a = a

Progress Monitoring

Progress monitoring is a scientifically based practice used to assess students' academic performance and determine the effectiveness of instruction. In progress monitoring the student's current levels of educational achievement are determined and academic goals are established. Appropriate interventions are used and the student's academic performance is measured regularly on a weekly or monthly basis. Progress toward goals is measured by comparing expected and actual rates of learning. Depending on the results of this monitoring instruction is adjusted appropriately.

set model

tangle objects or concrete models

Symmetric Property

If a = b, then b = a

Reflexive Property of Equality

a = a

Commutative Property of Multiplication

ab=ba

Associative Property of Multiplication

(ab)c = a(bc)

Commutative Property

a+b=b+a

Accuracy

how many problems a student can solve correctly

Flexible Grouping

Groups that change as the students' learning needs change

Interest Grouping

groups of students based on student interest

Summative Assessment

Assessment data collected after instruction to evaluate a student's mastery of the curriculum objectives and a teacher's effectiveness at instructional delivery.

Formative Assessment

Assessment used throughout teaching of a lesson and/or unit to gauge students' understanding and inform and guide teaching

Rules of Divisibility

2- even

3- sum of digits

4- last 2 digits

5- ends in 0 or 5

6- 2 and 3 works

8- last 3 digits

9- sum of digits

10- ends in 0

Volume

The amount of space an object takes up

absolute deviation

1.find the mean

2.find deviation, subtract each number and the mean.

3. find the average

linear

straight line

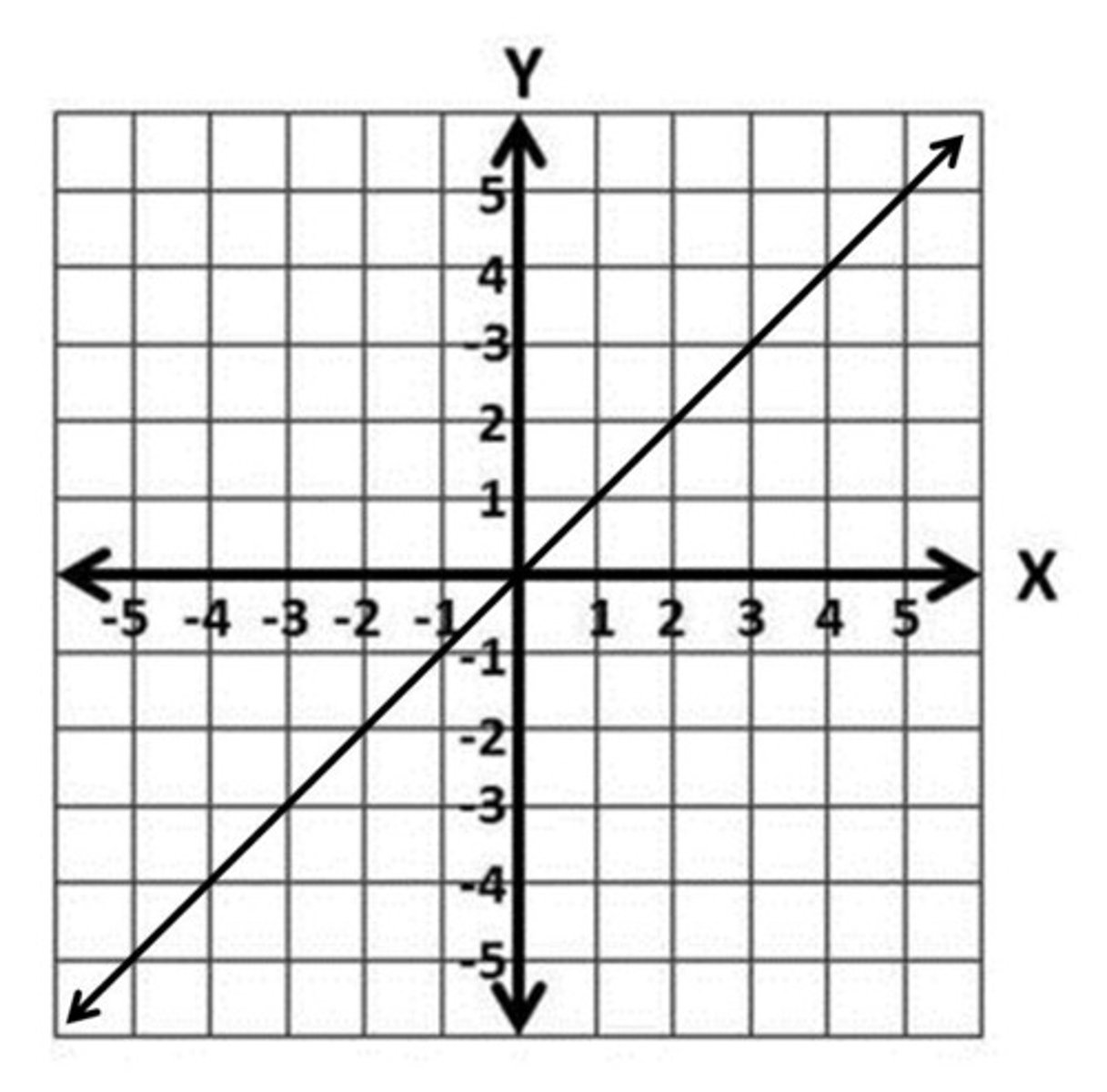
reasonableness

The result of a calculation or problem solving operation reflecting what is reasonable within the context or given factors or values. Checking the problem.

Power to zero

any number raised to the zero is always equal to one

Horizontal Line (4,6)

If the line runs horizontal, the Y coordinate stays the same. Therefore, any answer should have 6 as the Y coordinate.