Sample size reporting

What is statistical power?

The probability that a study will correctly detect a real effect (i.e., not miss it).

Why is high statistical power important?

Because it reduces the chance of false negatives — missing a real difference between groups.

Do most scientists know how to calculate power?

No. Only 20–30% of physicians and scientists can actually perform statistical power calculations.

Why do scientists care about sample size?

Because sample size directly affects power and determines whether a study is likely to detect real differences.

What happens if a study has low power?

Even if a real effect exists, the study might fail to find it, leading to incorrect conclusions.

What is random error in a study?

Natural variation that makes results miss the true effect, even when the study is designed perfectly.

How does sample size affect random error?

Small sample sizes increase random error and make results less accurate.

Sample size summary

Small sample = less accurate

because results bounce around a lot (random error).

Big sample = more accurate

because averages and confidence intervals stabilize.

Why do some confidence intervals in a study miss the true mean?

Because of random chance — even if the study is perfect, about 5% of 95% CIs will NOT contain the true mean just by luck.

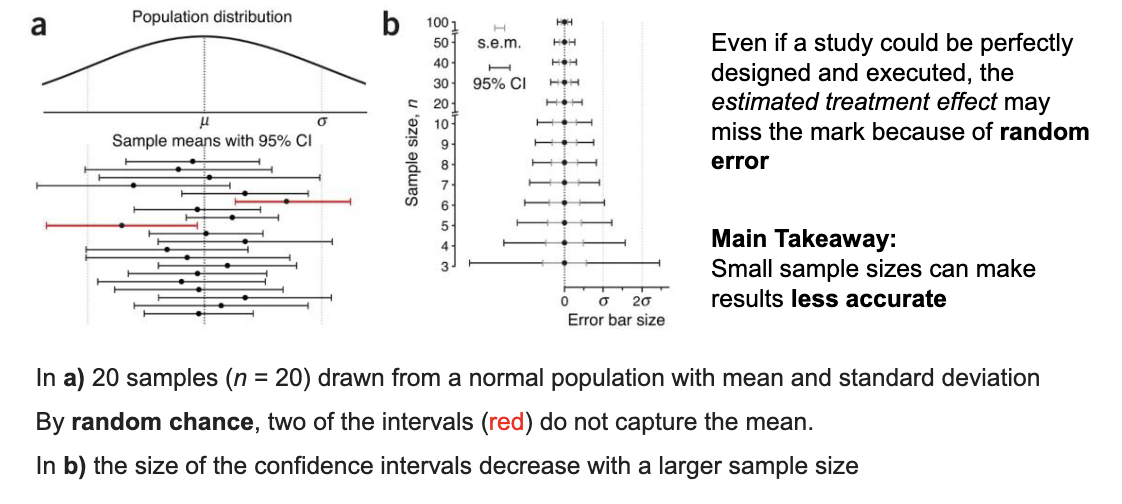
How does sample size affect confidence intervals?

Larger sample sizes = narrower (more precise) confidence intervals. Smaller samples give wider CIs, meaning less accurate estimates.

Why do clinical trials need to plan how many participants to include?

Because too few participants make results unreliable (risk of false positives or false negatives), while too many waste time, money, and expose people to unnecessary risk.

• they must plan how many participants to include before it starts collecting data

What happens if a trial has too few participants?

The study may fail to detect a real effect (false negative) or may show fake effects from random chance (false positive).

Why do trials enroll more participants than the minimum sample size?

To allow for drop-outs, so the final number of participants stays above the required amount.

What is the purpose of a sample size calculation in an RCT?

To control the risks of false positives (seeing a fake difference) and false negatives (missing a real difference).

• scientists usually accept about 5% false positive risk and 10–20% false negative risk.

• if we dont calculate sample size, we dont know if these risks of making the incorrect inference are large or small

What are the four components required for a proper sample size calculation?

if only general statements appear - like a large sample was recruited to ensure statistical power, you should question whether the estimate was rigorous 

When can you not skip the sample size calculation?

When the goal of the trial is to test whether a treatment actually works (its efficacy). You must calculate sample size for real effectiveness trials.

When can a sample size calculation be skipped?

In small pilot studies that only test feasibility — not whether the treatment works.

What does a “feasibility study” mean?

A small study (12–30 people) that checks whether a larger trial is possible (recruitment, safety, procedures), not whether the treatment is effective.

these answer questions like:

• Can we recruit enough participants?

• Is the dose safe enough for more people?

• Are our measurement methods doable in a real clinical setting?

Can pilot studies be used to prove that a treatment works?

No. They are too small and cannot make conclusions about medical effectiveness.

• cannot make conclusions about medical effect

What to check for in assessing the sample size reporting

Example for sample size reporting

HR < 1 → treatment is helpful
HR > 1 → treatment is harmful

It includes all 3 required parts of a proper sample size calculation:

• Significance level (5%)

• Power (88.7%)

• Effect size (HR = 0.80)

✔ It reassures the reader that the authors actually planned their sample size instead of guessing.

✔ It shows the study is statistically strong, because:

• 5% false positive risk is standard

• 88.7% power is higher than the usual 80%

• HR = 0.80 is a realistic, meaningful effect size

✔ It is transparent → you can actually see how they decided how many participants were needed.

Example for sample size reporting 2

This study is weak because it did NOT calculate the sample size.
That means we don’t know the risk of false positives or false negatives → so the results might be unreliable.

---

⭐ Why It’s Bad ❌ No sample size calculation

They didn’t decide ahead of time how many participants were needed.
So the study might be:

• Too small → missing real effects (false negatives)

• Too small → producing random false positives that look real

We basically don’t know.

In the discussion, they say:

“The interpretation of data from subgroup analysis is hazardous.
Number of patients… likely insufficient for statistical significance.”

But then in the conclusion, they claim:

“Ticlopidine is somewhat more effective…”

This is misleading because they just admitted the sample is too small to trust the results.

Because no sample size was calculated, we don’t know:

• Was the false positive risk 5%?

• 30%?

• 70%?

• If the study is too small, the risk of a false positive can be very high.

Example for sample size reporting 3

This study is weak because it used a very small sample size (only 23 people per group) and did not perform a sample size calculation. This means the groups may not have been comparable, the results could easily be due to random chance, and the risks of false positives or false negatives are unknown. Overall, the findings are not very reliable.

Example for sample size reporting 4

This study is unreliable because it used a very small sample size (only 46 people) and did not perform a sample size calculation. It was labeled a pilot study, which means it was only supposed to test feasibility—not effectiveness. However, the authors wrongly claimed that the treatment “demonstrated effectiveness,” even though the small sample makes any differences likely due to chance or natural differences in patients’ ability to heal. This creates a high risk of false conclusions.

Example for sample size reporting 5

This study claims to have a section called “Sample size calculations…” but no actual calculation is provided. Instead, the authors just say they enrolled 60 people (30 per group) without explaining why that number is appropriate.
Because no sample size calculation was done, we don’t know:

• the risk of false positives

• the risk of false negatives

• whether 60 people is enough to detect a real difference

This is a basic failure in clinical trial design and peer review, because readers cannot trust the results when the statistical foundation is missing.