calc

IVT condition

If f(x) is continuous on [a,b] and y is between f(a) and f(b),

IVT gist

• if the function is continuous over an interval and “y” is between endpoint y values, then there has to be a point in the interval where the function’s value equals y 

EVT condition

 if f(x) is continuous on the closed interval [a,b],

evt gist

any interval on a function has a max point and min point

inverse trig derivatives

speed up slow down

v and a signs

derivative of inverse

2nd deriv para process

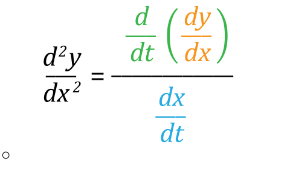
formula

MVT condition

if f is diff on (a,b) and cont on the [a,b],

MVT gist

• if the function is cont and diff on the interval, there is one point whose derivative is the same as the derivative of the whole interval (parallel tangent line to secant) 

rolles condition

 If f is diff on (a,b), cont on [a,b], and f(a) = f(b) = 0,

rolles gist

if the end points equal 0, then there is a point on the interval where the slope is 0 (rel min or max)

trapezoid rule

simpsons rule

trig integrals

length of a curve

parametric length of curve

polar length

polar area

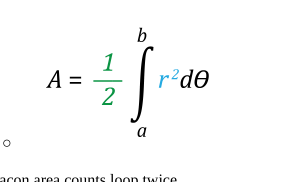
trig derivatives

mass formula

• mass = density * (length, area, or volume)

dot product

well known power series

integral test conditions

• function is positive, strictly decreasing, and continuous 

• to prove these, take derivative. if it exists, then cont, and if less than 0, integral decreases 

ratio test conclusiosn

• L is the limit as n approaches infinity of |term n + 1 over term n|

• if L < 1, series converges absolutely 

• if L > 1, series diverges 

• if L = 1, test fails

limit comparison test conclusions

• put the summand for unknown series on top of summand for known series 

• L is the limit of that quotient as n approaches infinity 

• if L > 0 then top converges/diverges based on if bottom does 

• if L = 0 and bottom converges, then top converges 

• if L = infinity and bottom diverges, then top diverges

combining series conclusions

• if both series converge, then sum converges 

• if one converges and other diverges, sum diverges 

• if both diverge, indeterminate

geometric remainder

• Rn = S - Sn 

• S = t1 over 1 - r (partial sum) 

• Sn = t1 times 1 - r to the n over 1 - r (nth term) 

estimate remainder integral test

• only if fulfils integral test conditions 

• take the integral from n (not n +1) to infinity of the function 

• remainder has to be less than or equal to that absolute value