Math: disc and washers, shells, length, surface area

Discs and washers

• When you draw them, it’s PERPENDICULAR

• In terms of x is dx

• In terms of y is dy

• It helps to draw things out

Discs and washers formula

π ∫ R²-r²

Discs and washers formula when you’re revolving around a specific line

DX if line is PARALLEL to x-axis = Top-bottom

DY if line is PARALLEL to y-axis = Right-left

SHELLS acronym 

SEO — search engine optimization but irl Shells Opposite

Opposite in that the axis and the differential are opposite

• Revolving around X axis = DY

  • But DY is in terms of y

• Revolving around Y axis = DX

  • But DX is in terms of x

SHELLS formula

2π ∫ (x)(f(x)) dx 

2π ∫ (y)(f(y)) dy

Shells around a specific line

Just add that line onto the x or y (not the function)

Shells HEIGHT when area is between two curves

Top-bottom DX

Right-left DY

Attach to actual function (not the x or y)

Length of a curve - remember

bounds are in x, then DX

bounds are in Y, then DY

Length of a curve formula

∫√1+derivative²

Surface area and formula

Revolving around X axis: DX

Revolving around Y axis: DY

Formula: 2π ∫ f(x) • derivative²

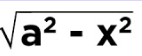
x = asinθ

cos²θ = 1 - sin²θ

like 1-x²

You can remember because the 1 at the start is like the beginning and like sin is the first one

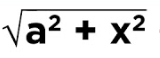
x = atanθ

sec²θ = 1 + tan²θ

Can remember because this is the only one with + and “t” in tan looks similar

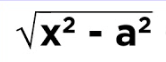
x=asecθ

tan²θ = sec²θ - 1