CSE 12 Midterm 1 Key Information

Voltage

Unit: Volts (V)
—> The potential difference between ends of the circuit

Current

Unit: Amperes (Amps) (A)

—> The rate of flow of the electrons in a circuit

Resistance

Unit: Ohms (Ω)

—> Resistance the flow of electrons must overcome

Electrical Charge

Unit: Coulomb (C)

—> the amount of electricity conveyed in the circuit by one ampere,

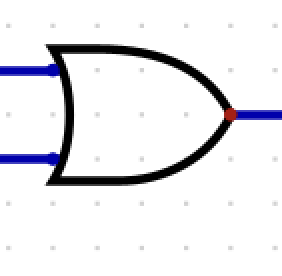
What is this?

OR

A + B

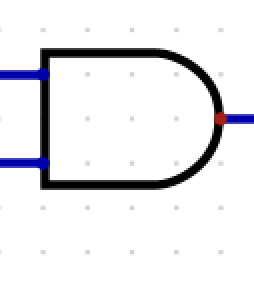
What is this?

AND

AB

What is this?

Inverter

A’

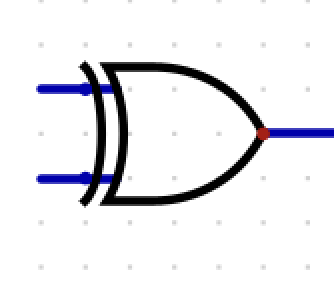
What is this?

XOR (Exclusive OR)

(A + B) * (AB)’

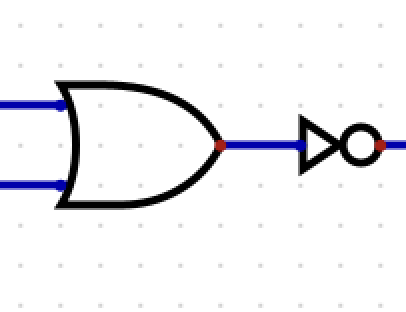
What is this?

NOR

(A+B)’

A’B’

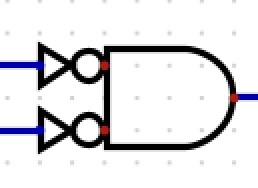
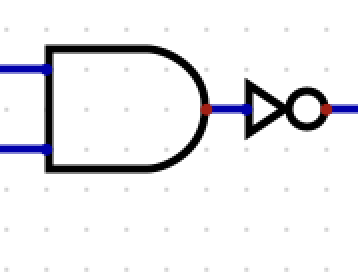
What is this?

NAND

(AB)’

A’ + B’

Vdd

Maximum voltage in the circuit

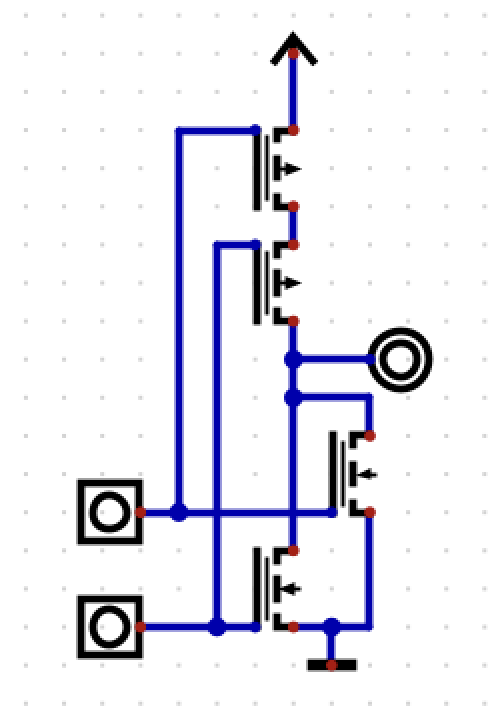
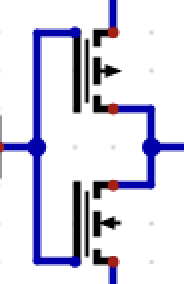
Switches in parallel

OR (PMOS)

NOR (CMOS) Shown in the image

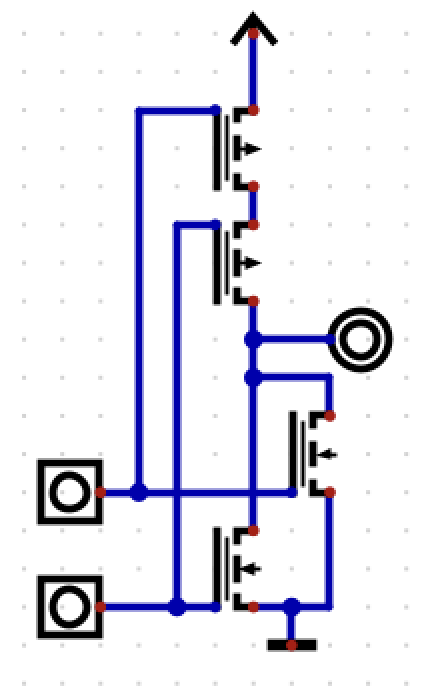
Switches in series

AND (PMOS)

NAND (CMOS)

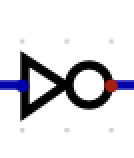
What is this?

PMOS “NOT”

In: 1 —> 0

In: 0 —> 1

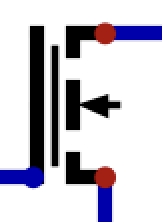
What is this?

NMOS “TRUE”

In: 1 —> 1

In: 0 —> 0

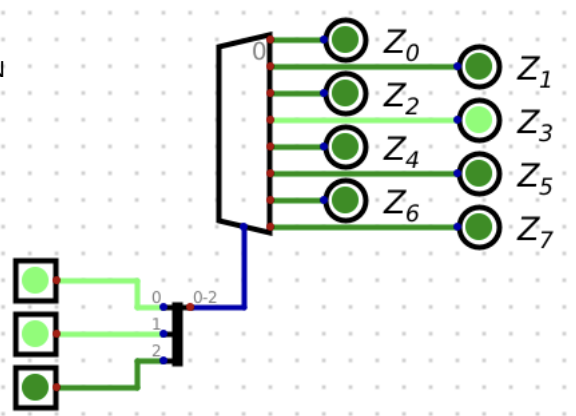
What is this?

Decoder: n inputs, 2ⁿ outputs of all minterms (combinations of inputs)

Used to:

1) generate a “one hot vector”: minterm where ONLY one bit is 1.

2) Converts memory or registers an address to a control line

3) Converts an opcode to n control lines (numerical representation of a command)

Section lines / Control lines

Number: log₂(n) of the multiplexer’s inputs

• input lines “conditional inputs” needed to narrow the n inputs to one output in a multiplexer

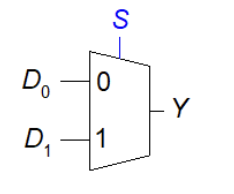
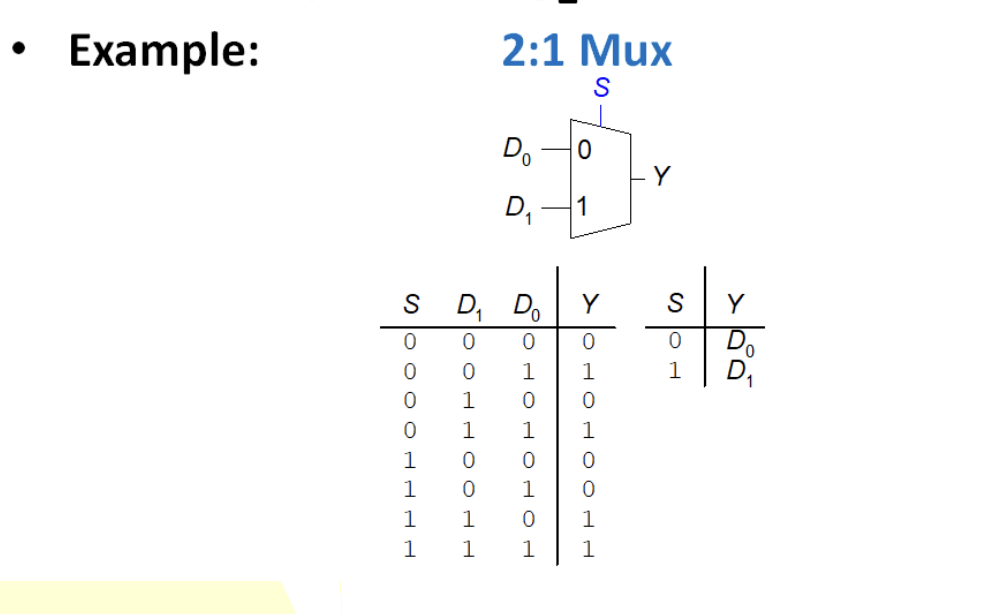
What is this?

Multiplexer

• Outputs log₂(n) bit-long output from n-bit inputs

• Selects one of n inputs to send to control lines

• Possibility to encode more than one input value into a multi-bit output value.

Minterm

Product that includes all the inputs (inverses of inputs are fine)

• A term in the sum of products

ex. Inputs A,B,C

Minterms: ABC, A’BC, A’B’C, A’B’C’, ABC’, etc.

Maxterm

Sum that includes all the inputs (a term in the product of sums).

Multiplexer implementations

1) 2-Level: using AND, NOT, and OR gates to get a single output out of n inputs.

2) Tristate: Using tristate to select one of many inputs to send to an output.

3) Hierarchical: Using 2:1 multiplexers to simplify n to log₂(n), use 2:1 multiplexers on next in series to simplify to one output at the end.

Sum of Products

Depicts all possible values of the inputs that are outputted as 1 (TRUE).

• Used for NMOS sides of CMOS gates.

1) Look at truth table, find lines with TRUE as their output

2) take the product of all the inputs for each line.

3) Sum the products.

Product of Sums

AND combination of all the inverses of the terms (and combos) that would yield a zero.

• The PMOS reflection of a true combination.

1) Find the rows with zero (FALSE) outputs

2) For each row, sum the invested of every single input in that line.

3) AND multiply the sums for the product of the sums.

Axiom Dual

For any axiom: Replace * with + and A with A’ (or vice versa)

B = 0 if:

B = 0 if B ≠ 1

0 * 0 =

0 * 0 = 0

Dual: 1+1 = 1

1*1 =

1*1 =1

“AND” gate

Dual:

0 + 0 = 0

0*1=

0*1 = 1*0 = 0

“OR” gate

Dual:

0+1 = 1+0 = 1

B * 1 =

B * 1 = B

Dual:

B+0 = B

B*B =

B* B = B

Dual:

B + B = B

(B’)’ =

(B’)’ = B

B*B’ =

B*B’ = 0

Dual:

B + B’ = 1

BC =

BC = CB

Dual:

B+C = C+B

(BC)D =

(BC)D = B(CD)

Dual:

(B+C)+D = B+(C+D)

B*(C+D) =

B*(C+D) = BC + BD

Dual:

B+(CD) = (B+C)(B+D)

B * (B+C) =

B * (B+C) = B

Dual:

B+(BC) = B

BC + BC’ =

BC + BC’ = B

Dual:

(B+C)*(B+C’) = B

DeMorgan’s Theorem

• Key to any CMOS construction: a PMOS (PUN) / NMOS(PDN) and its dual.

(ABC)’ = A’ + B’ + C’

(A+B+C)’ = A’B’C’

Why is CMOS more popular than NMOS or PMOS?

CMOS is always connected to either ground or Vdd — AT NO POINT is there a current buildup on a single resistor —> Less overheating.

Floating Outputs / Floating Nodes

Denoted by Z

• Might be 1, 0, or in-between 1 and 0 volts.

• Caused by resistance in the circuit stripping away magnitude from Vdd.

—> Voltmeter’s DON’T DETECT Floating outputs/nodes.

—> Used for Tri-state Busses (Delivering one or more bits from one output node to several receiving nodes)

What is this?

NMOS Pass Gate

(Non positive feedback loop/ “non-regenerative”)

What is this?

PMOS Pass Gate

(Non-positive feedback loop/ “Non-regenerative”)

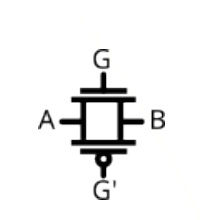
What is this?

Full Transmission Gate

• Non-regenerative (no positive feedback loop)

• No voltage threshold loss (same principle as CMOS)

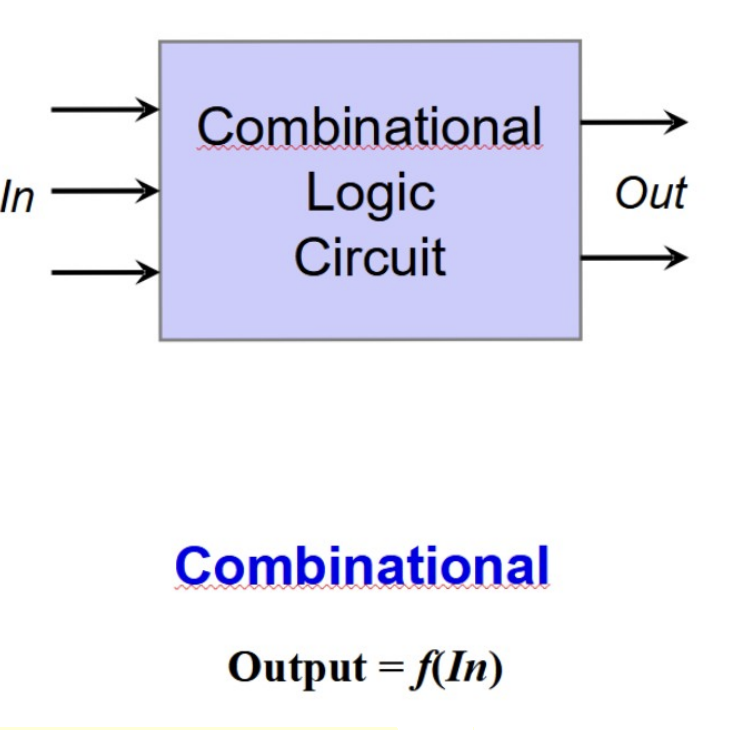
Combinational Logic Circuit

Circuit with no memory capability (no positive feedback looping), a “Stateless” machine.

• Same out put for given set of inputs

• Ex. Adder with Carry out and Sum out.

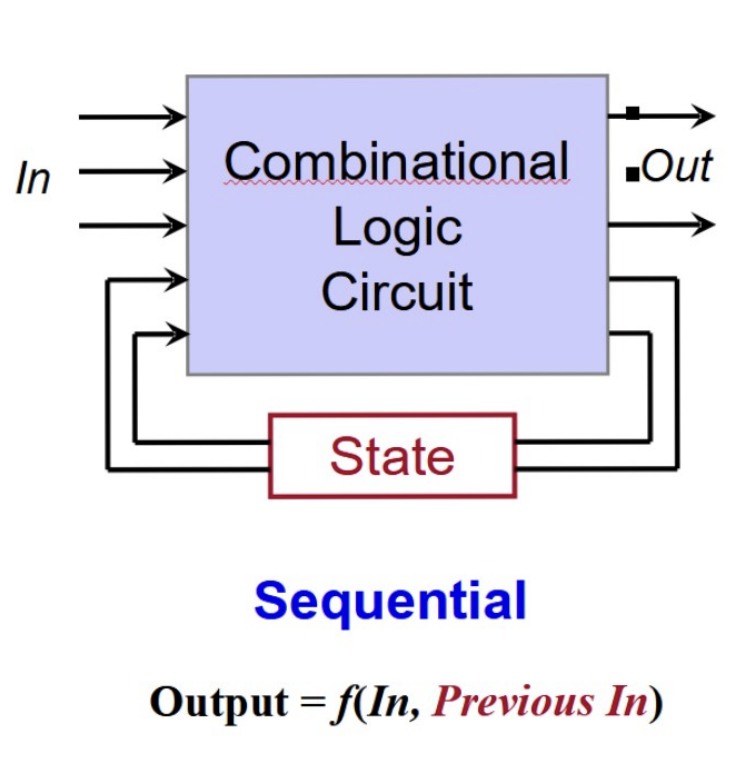
Sequential Logic Circuit

Circuit with feedback looping or “State” machines

• Output depends on a SEQUENCE of inputs (past and present)

• “Remembers” inputs previously with its “state”

• NOTE: Alternative way to store memory w/o positive feedback loop: Capacitor storing charge

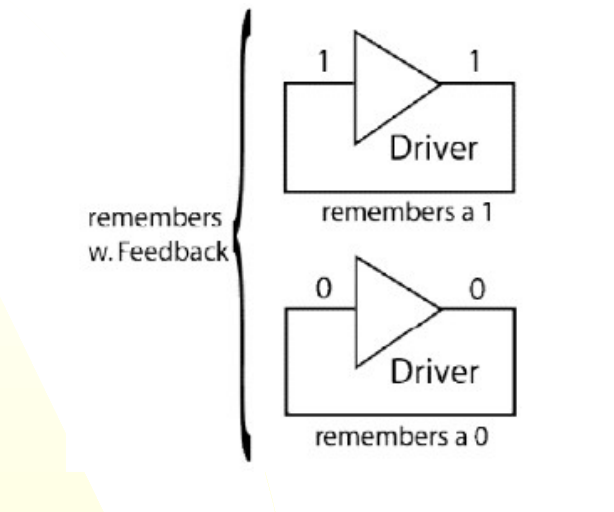
How do state machines work? How can you cell the function of a state machine?

Driver in a loop with itself ie. output of the driver goes to the input of the driver

• The driver keeps repeating the inputted signal to itself before it is referenced again.

• CANCELLING: Driver + inverter —> the signal flips every time it is repeated into the driver and the original signal is lost.

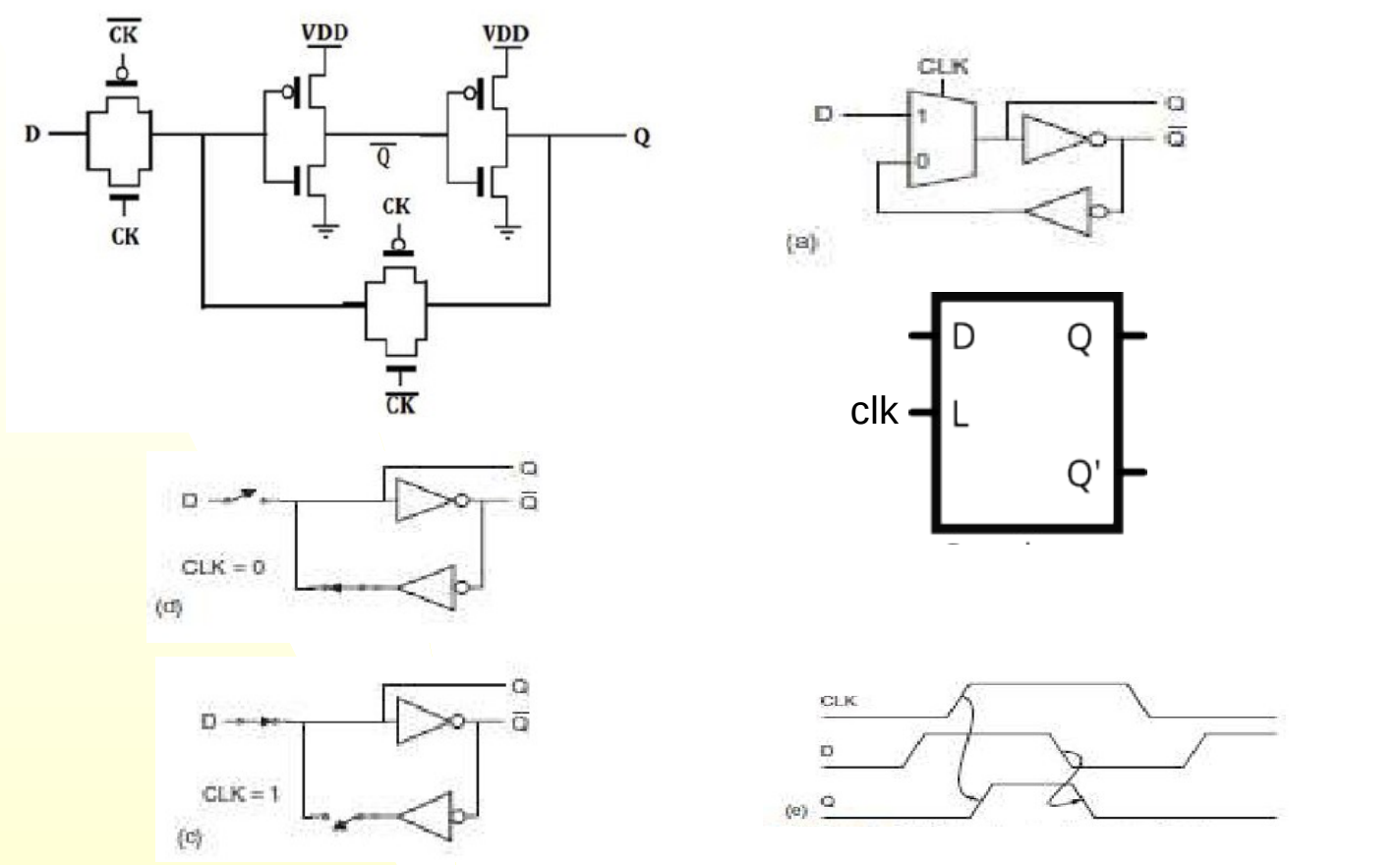
What is this?

See-through D-latch:

• When the enable signal is 1, allows input d to go directly to output Q (hence the “See-through”)

• When enable signal is 0, it “remembers” the last d value when enable was 1 and sends that to output Q.

What is this?

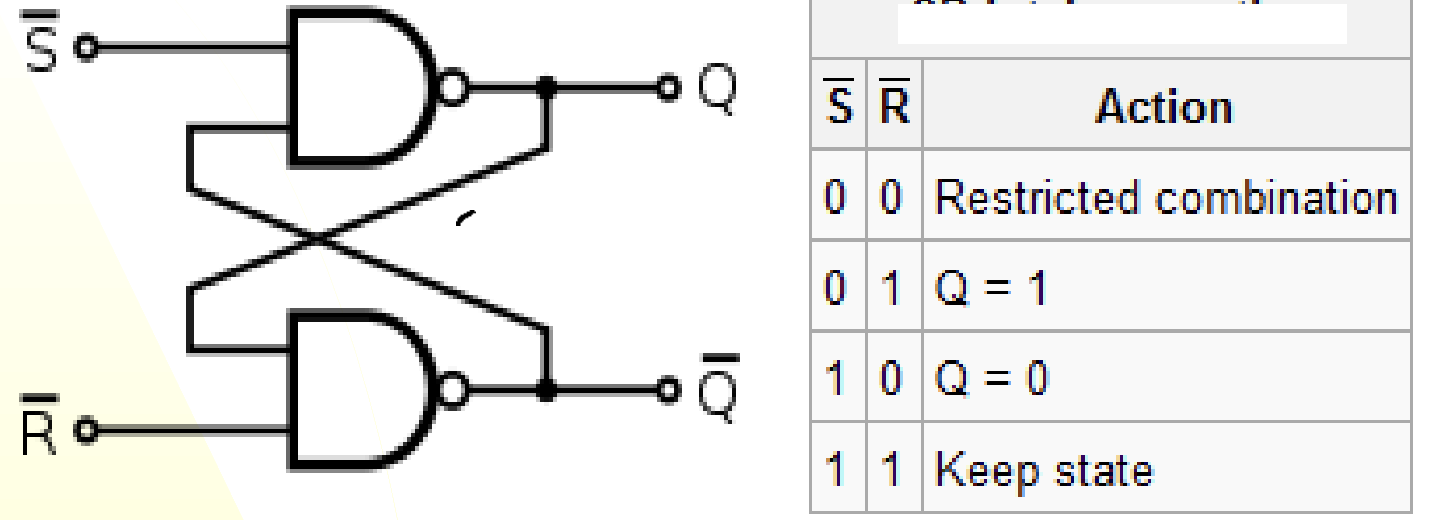
NAND SR Latch (“Set-reset latch”)

• One input controls whether the value is set. (S)

• The other controls whether the value is cleared. (R)

  S = 0, R = 0 is an undefined output (non-functional)

• S = 1, R = 1 keeps the state of the input.

• SR’ —> Q = 1 or S’R —> Q = 0

What is this?

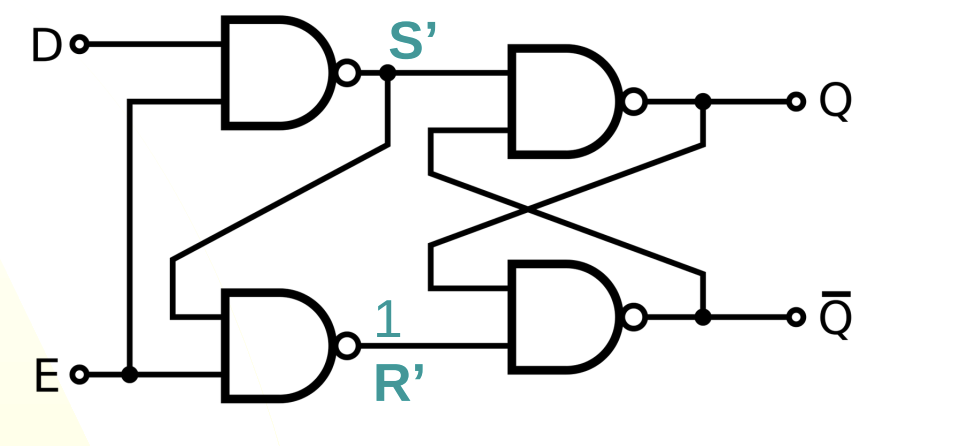
SR NAND D-Latch

• Resets to D when E = 1, else it retains its previous value.

What is this?

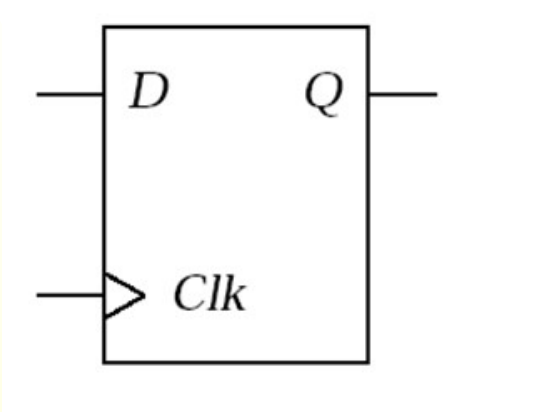
Positive edge-triggered Flip-flop

• TRIANGLE IMPLIES EDGE TRIGGERED

• When the Clock (Ck, the eval input) goes from 0—>1, then the system resets as D.

• In ANY other circumstance, the flop does not flip.

• EASY TO USE compared to see-thru gates (edge input is the only variable, D can be handled separately.)

What is this?

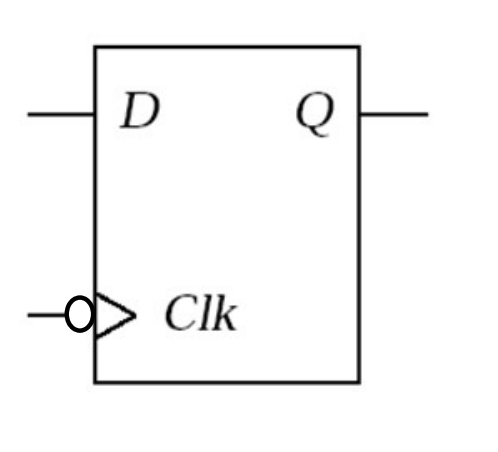
Negative edge-triggered D flip-flop:

• when the clock (eval edge labeled “clk”) goes from 1—>0, the stored data is reset to D and then looped until the next “falling” edge.

• NO OTHER clk inputs will make it change.

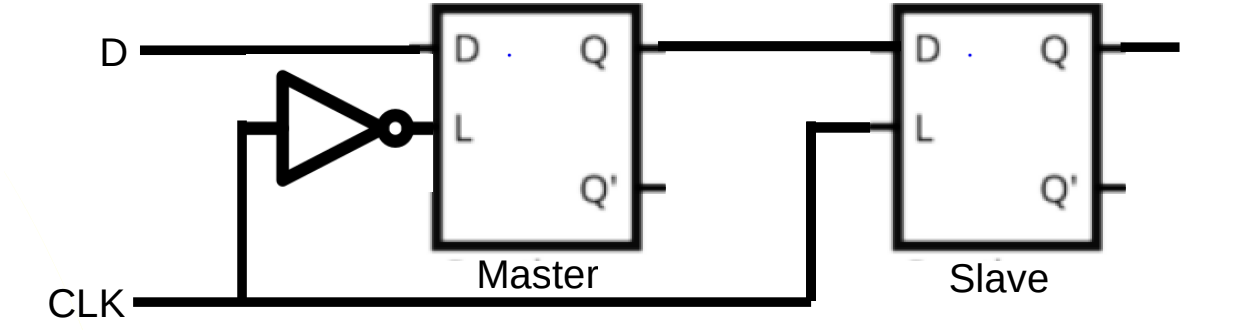
What is this?

Positive edge-triggered latch

• When the Clk = 1, signal is immediately passed through D to Q

• Else, the D see-through latch locks.

• “master” clock controls flow, “Slave” clock controls D.

• “MASTER” clock: positive clock, “SLAVE” clock: negative clock

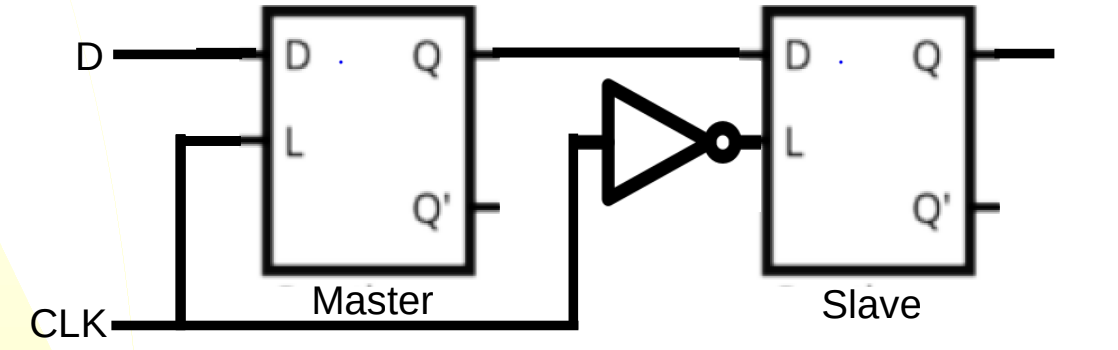
What is this?

Negative edge-triggered D-latch

• Circuit is completed ONLY when Clk goes to 0

• Else, it is locked.

• “master” clock controls flow, “slave” clock controls D.

• “MASTER” Clock: negative clock, “SLAVE” clock: negative clock.

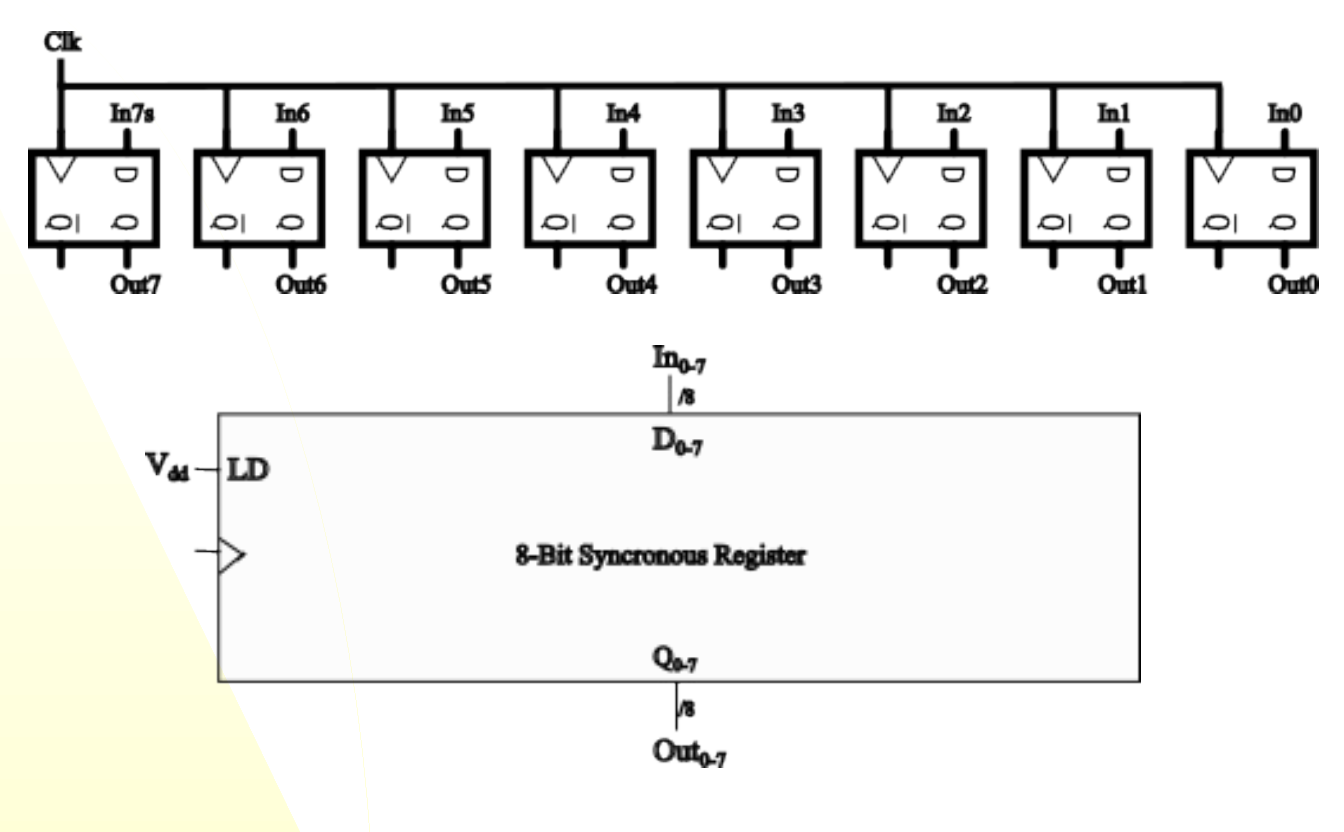
What is this?

Synchronous register

• Allows for parallel processing of the data (Registers can only store one bit, synchronizing registers gives the ability to process more than one bit).

• Uses a clock to synchronize (time and work together) operations on bits.

• Type of Shift register (because positive-shift or negative-shift edge register)

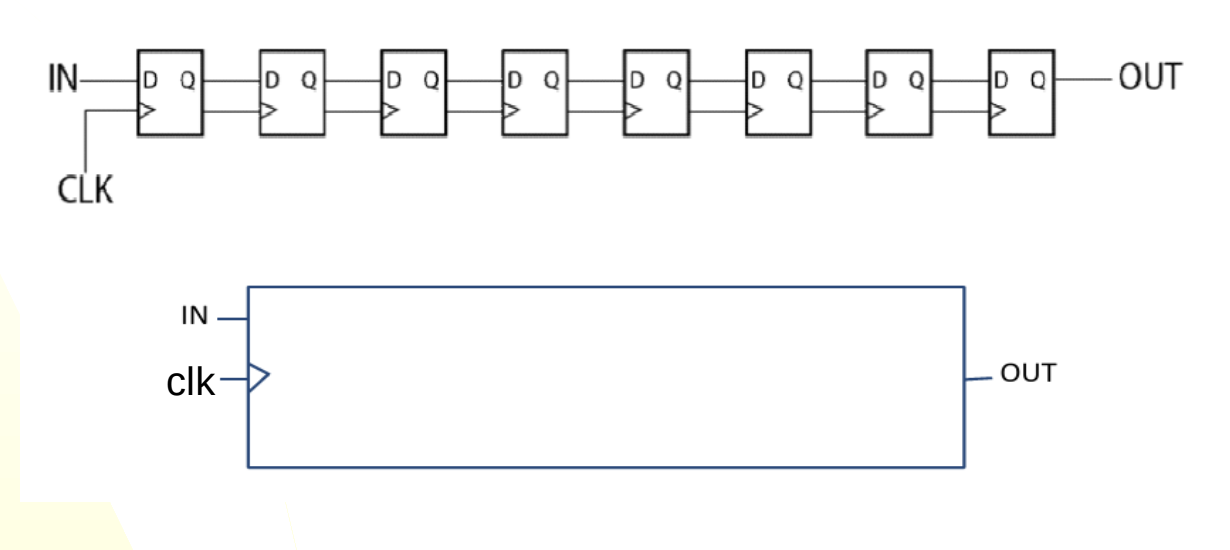
What is this?

Synchronous Register

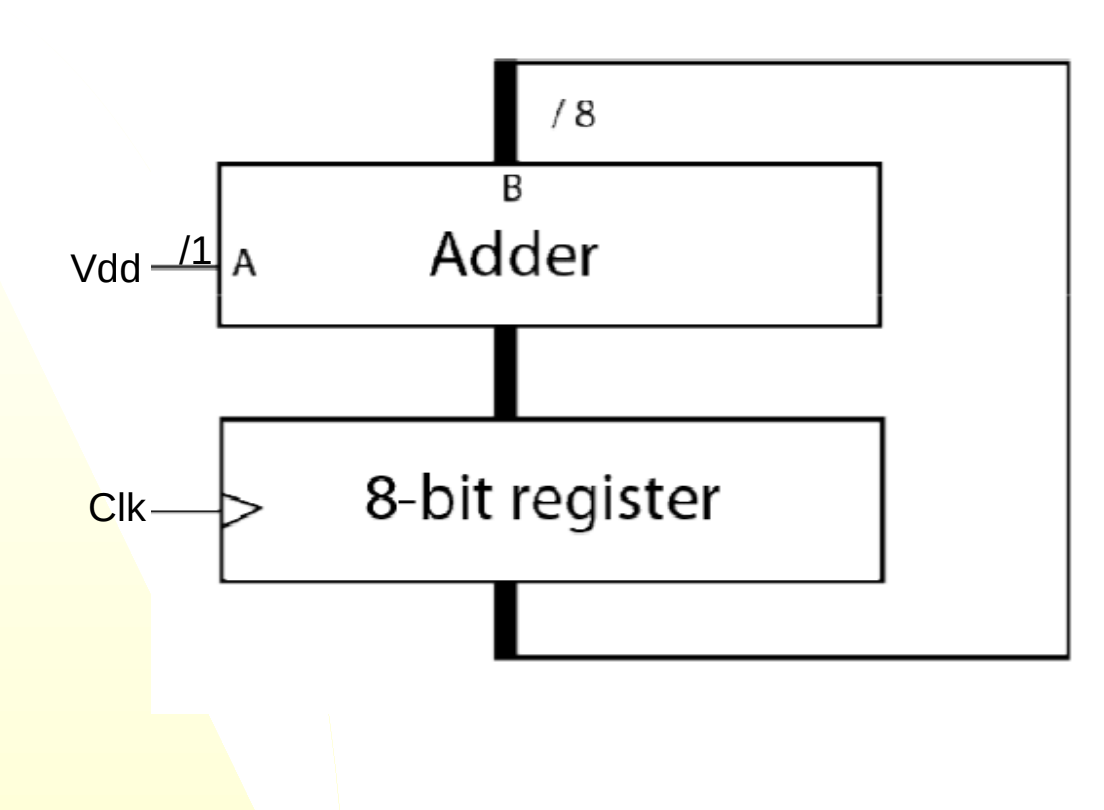
What is this?

A counter

• Increments or decrements a saved (registered) value according to the pulses of the clock.

Binary

Base-2 language of computers

• only 1 or 0 for 1 volt or 0 volt across recievers

• combinations of 101-strings to convey complex data to registers.

Bit

1 digit of the binary string

• 2 possibilities: 0 or 1

• KEY: 2ⁿ possible arrangements of n bits

Byte

8 bits

Number of bits of storage (characters, numbers, addresses)

Chars: 8-16 bits: 2³- 2^4 bits

Numbers: 32-64 bits: 2^5 - 2^6 bits

addresses: 32-64 bits: 2^5 - 2^6 bits

Integer representations

1) Unsigned integers

2) One’s complement (Archaic)

3) Two’s complement

Unsigned integers

Represents ONLY positive integer values in BINARY.

• Records up to 2ⁿ-1 distinct values (one place being saved for the zero value, ie. zero indexing.)

Signed integers

Positive and negative values encoded in the number IN BINARY.

• One bit represents the sign (this is the “most significant bit (MSB)”):

  • MSB = 0 → +

  • MSB = 1 → -

• Range: -(2ⁿ-1) to 2ⁿ-1

Additive Inverse

Invert the sign bit on a signed integer.

One’s complement

Archaic

• Negation of the positive signed numbers, inverting all bits on the positive unsigned version of that number

• Wastes a bit value because there is a positive and negative zero with this system.

• The top bit is the MSB or “sign bit”

  • All other bits are magnitude.

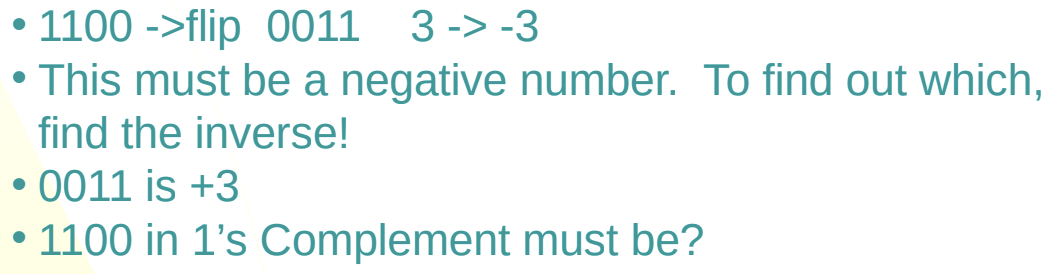
Two’s complement

Represents positive and negative signed integers

Range: -2^n-1 to 2ⁿ-1

• NOTE: largest negative number in 2’s complement bit range can’t be converted to positive in that bit range. (this is the “integer overflow” condition)

• Does not contain negative zero, saving machinery compared to 1’s complement.

• Positive: positive unsigned binary number, same as ever

• Negative (converting to binary and evaluating binary): invert all bits of the positive number, add one to the new binary number.

• ADDITIVE INVERSE (negation): One’s complement of the number, add one.

Sign Extension

Increasing the number of bits, but keeping the binary value those bits represent and their signs.

• Makes processing work with registers of different sizes.

• Process: add 0 bits in between the MSG and binary magnitude representation until the number of bits is satisfied.

  Ex. 0001 = 1 in 4-bit, 00000001 = 1 in 8-bit

  Ex. 1001 = -6 in 4-bit 2’s complement, 111110001 = -6 in 8-bit 2’s complement

Bitwise Logical operations

NOT the same as Language logical operations.

• Language logical operations are performed on explicit boolean values (true, false)

• These are used for binary numbers and the like.

• Done IN PARALLEL with corresponding bits in the data.

Bitwise NOT

~

ex. ~101 = 010

Bitwise AND

&

Ex. 0011 & 1010 = 0010

Bitwise OR

|

ex. 0011|1010 = 1011

Bitwise XOR

^

ex. 0011^1010 = 1001

Binary Addition

Like decimal addition. Carry the 1’s over to the next exponent place if the limit in one sections reached.

Implemented:

• Full adder cells.

• 3 inputs: Carry-in (for carrying into the addition from the last bits), a (input number 1), b (input number 2)

• 2 outputs: Sum (total number), Carry-out (if there’s a carry to the next highest bit)

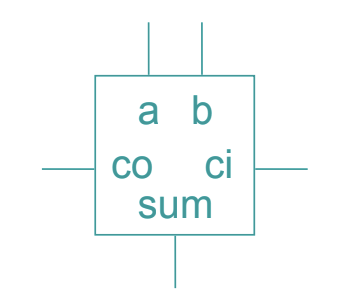
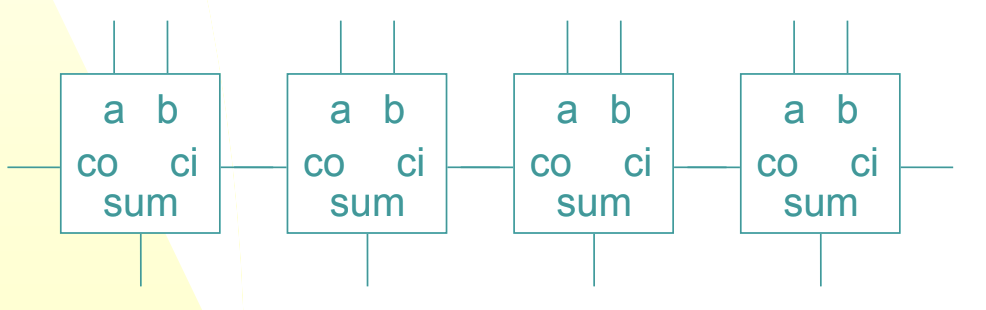
What is this?

Ripple-Carry adder

full-adders pass along the carryout into the carrying for the next adder (wired in series because all must be passed through)

• time taken proportional to number of bits (LOTS of time)

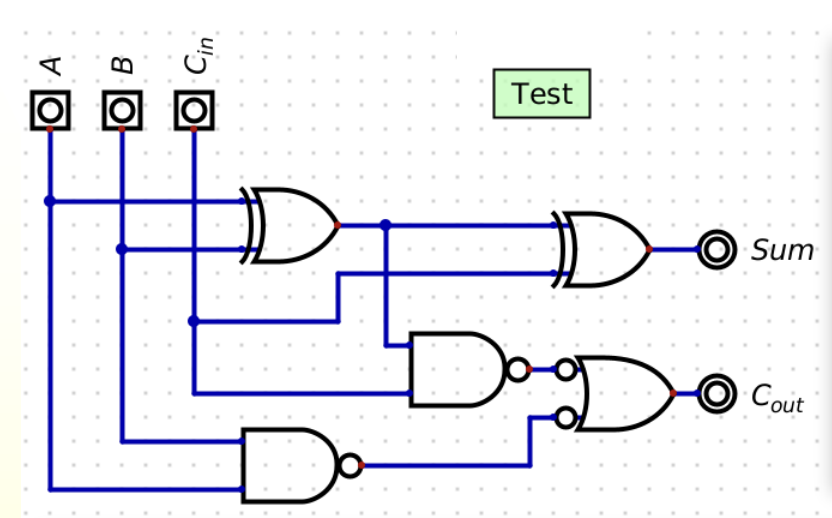
What is this?

Full adder

Calculates the sum of two binary numbers in binary

• 3 inputs, 2 outputs

• Sum = A xor B xor Cin, Cout = Majority(A,B,Cin)

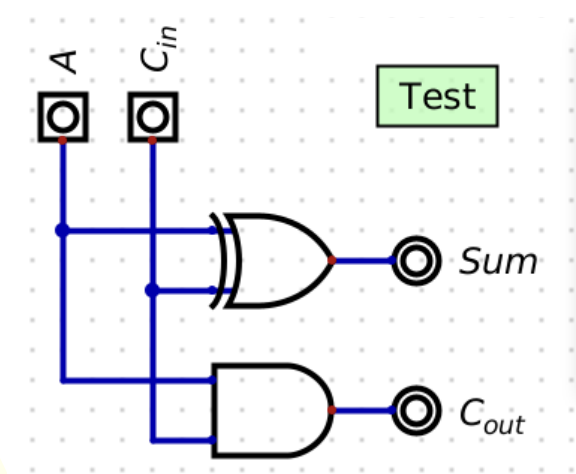
What is this?

Half-Adder

Used for counting up by increments of 1.

• Sum = A xor Cin, Cout = A and Cin

Adding in Binary

1) Unsigned: no issue, like standard addition (The carry-out IS KEPT as the “leading” number of the binary sequence ON TOP OF the resultant sum.)

2) SIGNED, 2’s complement: same as unsigned addition, BUT ignore the carry-outs on the very end if it doesn’t fit within the bit number. (see image)

Subtraction in Binary

Treat the subtractant in 2’s complement (fully make it negative), then add the two numbers.

• If there’s a carry beyond the total number of bits, ignore it (for SIGNED AND UNSIGNED SUBTRACTION)

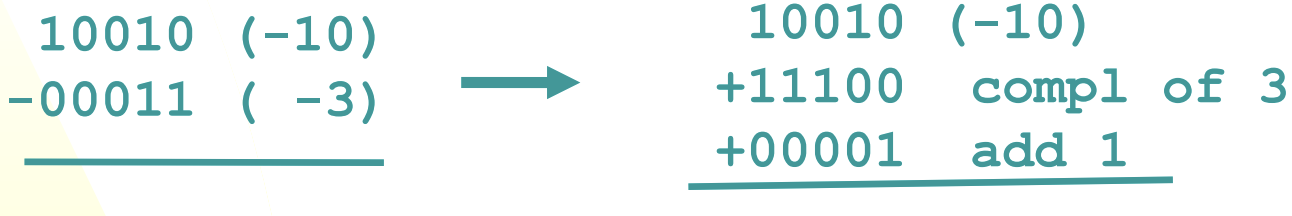
Binary

Base 2 (0-1)

Octal

Base 8 (0-7)

• Binary to Octal: Group binary starting at far right into groups of 3. Evaluate those groups of 3. The result is your number in octal.

• Octal to binary: split each octal bit into three binary bit representations of that octal bit’s number.

Hexadecimal (hex)

Base 16 (0-9, A-F)

• Binary to hex: Group the binary from far right to let in groups of four. evaluate those groups of 4. what remains is the number in hex.

• hex to binary: split each hex number into its representation in 4-bits of binary.

• Used to represent color values in RGB GUIs.

• Used to create a multi-valued truth table.

Shifts

Operations moving bits to the right or left.

Logical Shifts

Treat operands like unsigned numbers. Do nothing to the signed bit, except include it in the move.

• In effect, dividing (or multiplying) by powers of 2

• Moves terms n times to the right or left, preserve order and pattern unless “fallen” off of the right side or “fallen” off the left side.

• Replace space shifted rightward on the far left hand side with 0s, or space shifted leftward with 0s. (Logical shift left, see image)

Arithmetic shifts

Operations shifting according to the sign bit and sign extension.

• In effect, dividing (or multiplying) a signed number by powers of 2.

• RIGHT: Preserve order and pattern of the original number and shift n place to the right. If digits “fall off” the right side, ignore it.

  —> Fill the space left over from the shift with the MSB’s indicated sign of the number.

• LEFT: Preserve order and pattern of the original number and shift n places to the left. If digits" “fall off” the left, ignore it.

  —> Fill the space left over from the shift with 0s.

• NOTE: LEFT shifting has the chance to create overflows.

  —> python: rounds toward negative infinity if remainder left over in integer division

  —> C: truncates towards 0 if remainder left over in integer division.

Rotations

Move data from one end to the other.

• Treat operands being rotated as unsigned

• MSB is not treated with any special regard

Decimal to Binary

Use repeated divisions

• Divide the decimal number by 2 —> record the remainder of this

• keep dividing by 2 until the quotient is 0. Write the remainders in reverse order (remainder gotten last at the far left and remainder gotten first at the right). this is your binary number.

Any base to any base

Convert from the first base to base ten, then the base ten to the desired second base.

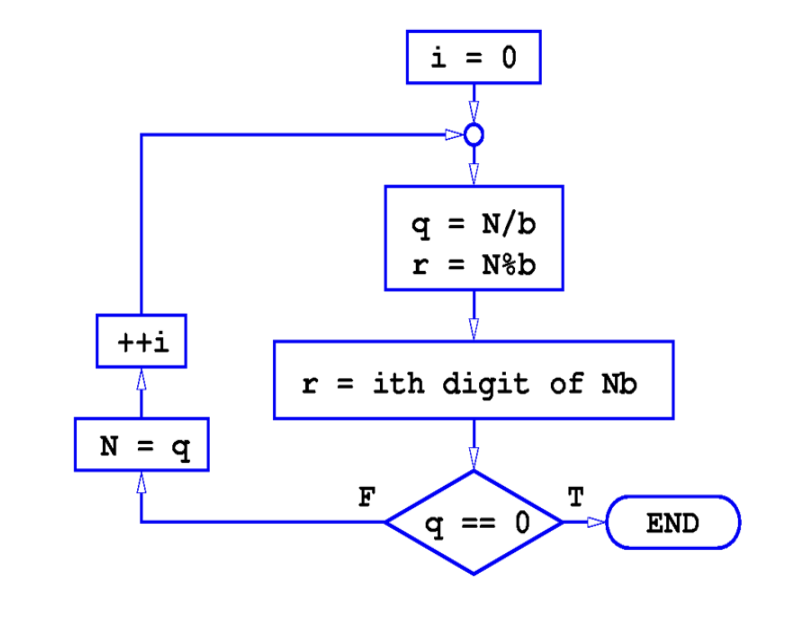
How many bits are necessary to express a number n in base b?

log_b (n) bits are needed

ie. (log(n)/log(b)) bits are needed.

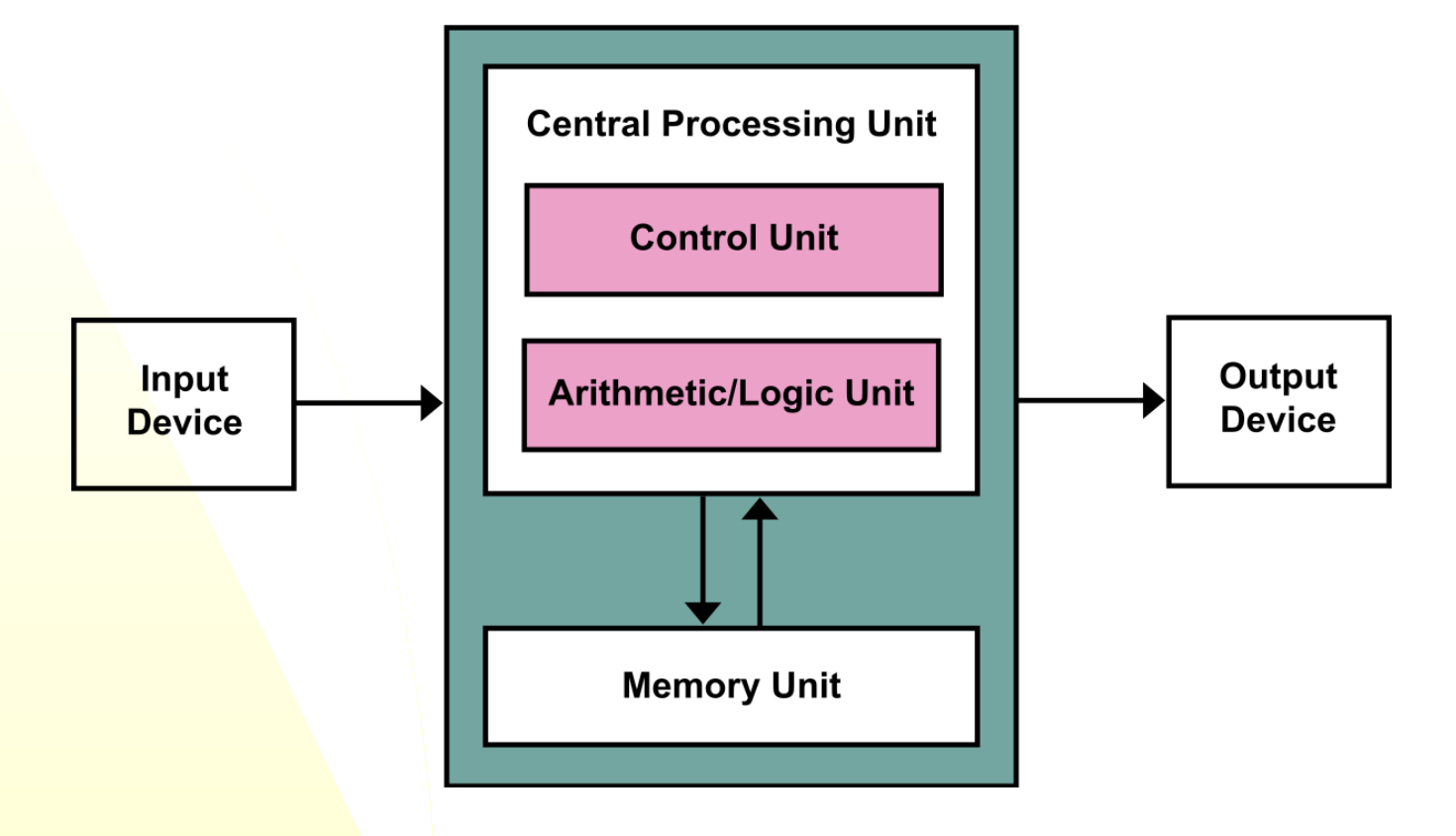
What is this?

The Von Neumann Model

CPU

Computer Processing unit

• RALU (Register Arithmetic Logic Unit)

• Arithmetic and logic unit (ALU)

• General Purpose Registers (GPRs)

  —> Control unit

• Program counter

• Branching Logic

• Instruction register

Stored programs

The backbone of every computer theory; a set of instructions and executables that can be stored in a computer’s memory.

CPU Memory

Stores Data, program instructions (a set of 1s and 0s that is 32 bits is RISC-V)

• GPRs are temporary storage for data being processed but the ALU.

• NOTE: MAIN MEMORY IS NOT IN THE CPU

Main Memory

Ultimate destination and origin of data and instructions

Addresses

Data in the main memory is referred to by its addresses (within directories and subdirectories of the memory)

• “Bit patterns that uniquely identify the location of a memory”

• Contents: Bit pattern stored at that address

Number of bytes in a word

4 bytes (32 bits)

Addressability

Number of bytes of memory being called at a certain address.

• RISC-V is byte addressable.

Overflow in addition

When in addition operations causes the signs to change unreasonably; ie. binary adding two negative 2’s complements results in a positive 2’s complement, (or adding two positives and getting a negative result) this is “overflow” and is not a valid addition result.