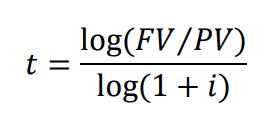The concept of the Present Value

Future value generic formula

𝐹𝑉 = 𝑃𝑉 × (1 + 𝑖) ^t

i = compound iterest rate, t years

(1+i)^t is the compound factor

Risk premium

= The additional return an investor expects to earn from an investment, to compensate for the higher risk as supposed to a risk free- asset

Return

= Profit/ initial investment

NPV

= How much profit( in todays money) an investment will make you, after covering the cost.  If it >0 do it

Discount factor

= 1/(1+i)^t : converts FV into Present terms

Perpetuity

= Cash flow that pays a fixed amount forever e.g. trust fund

PV of a perpetuity at year t=0 :

CF / i

cash flow per year / interest rate

𝐏𝐕 𝐨𝐟 𝐩𝐞𝐫𝐩𝐞𝐭𝐮𝐢𝐭𝐲 𝐝𝐮𝐞 𝐚𝐭 𝐲𝐞𝐚𝐫 𝐭 = 𝟎:

If the perpetuity starts immediately, it is called perpetuity due

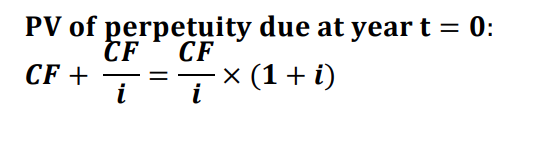
Growing perpetuity

Cash flow stream continue indefinitely and the cash flow amount is increasing at a constant rate

e.g. You are promised a payment of $500 next year, which will grow by 3% annually foreve

Annuity

An asset that pays or u pay, identical cash flows at regular intervals e.g. 500 a year for 5 years car

Calc annuity formula

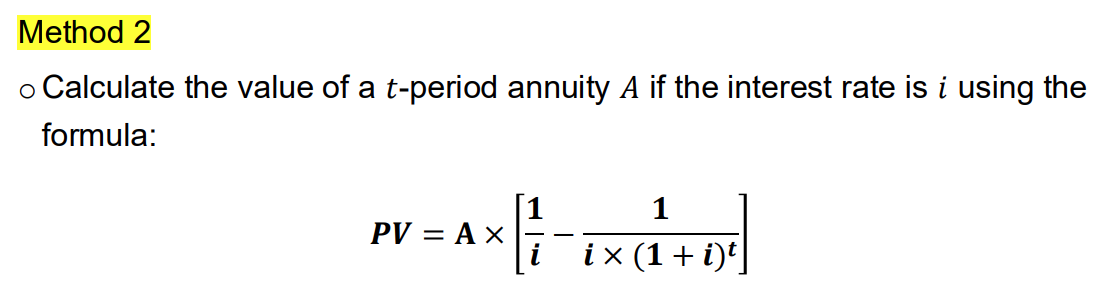
Annuity factor

accumulates the effects of discounting each equal payment back to the present. So if you're receiving $X per year for nnn years, the present value is:

PV=X×Annuity FactorPV = X \times \text{Annuity Factor}PV=X×Annuity Factor

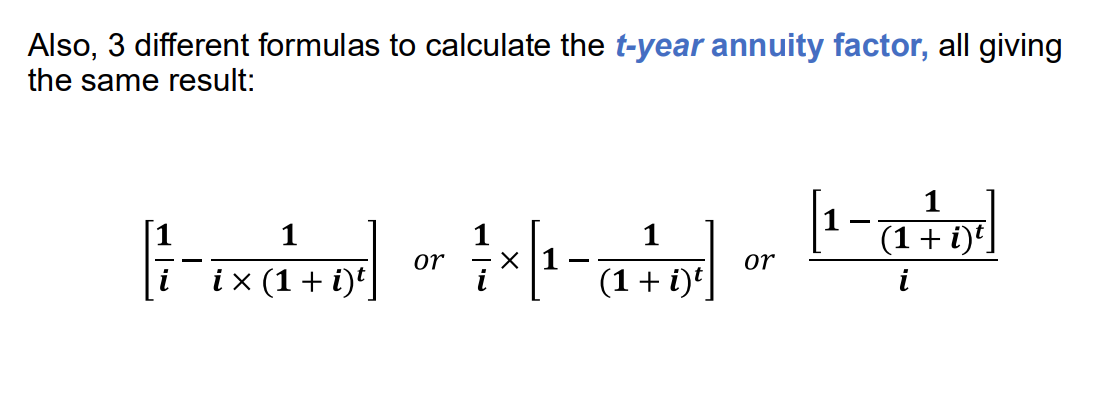
annuity due

Growing annuity + PV eq

a finite stream of cashflows (for 𝑡 years) growing at a rate g

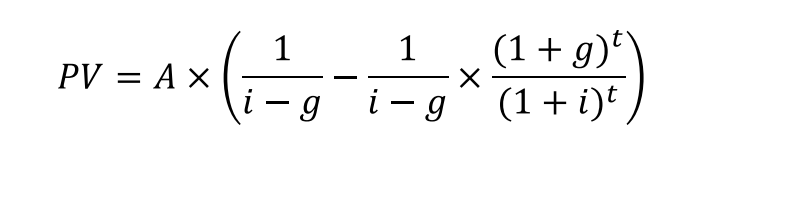
• Amortizing loan

• = Loan paid off in equal instalments

• Each instalment = interest + principal

• Common in mortgages, car loans, personal loans

Effective annual rate or annual percentage rate (APR)

we started with £1,000, and after 1 year of monthly compounding, the amount grew to £1,268.24. So, an annual compounded rate of 26.82% (this is called the effective annual rate or EAR).

APR = Annual percentage rate so new vs old year e.g. 0.268

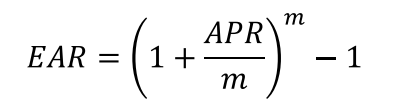
the present value of £1 received at the end year 𝑡 when the continuously compounded rate is �

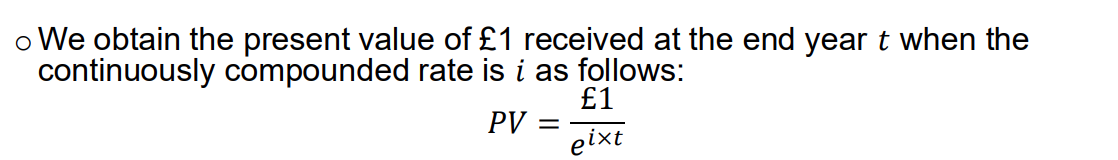
How long will it take for an investment to reach a multiple of its initial value, given a constant annual interest rate ii?