Chapter 17: Oscillations

Features of oscillating motion

• Equilibrium: Point at which object starts

• Amplitude (m): Distance from equilibrium

• Period (s): Time taken to complete a full oscillation

• Frequency (Hz): Mumber of complete oscillations per unit time

Phase difference

Difference in displacement between two times of an oscillation

Angular Velocity

Amount of turn undergone per unit time

Angular Frequency in oscillations

ω = 2π / T

ω = 2πf

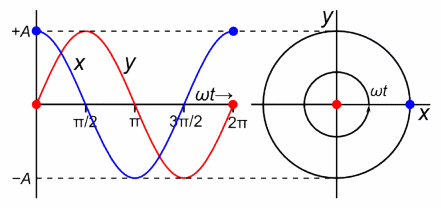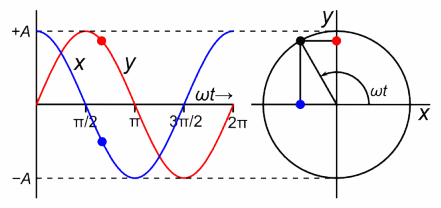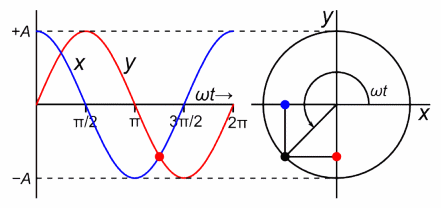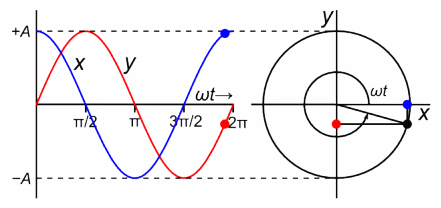
Simple Harmonic Motion

Motion whereby the acceleration is given by

a = -ω²x

• ω is a constant for the object

• a ∝ x

Isochronous oscillator

An oscillator whereby the period of oscillation is independent of the amplitude

• This is because as amplitude increases, average speed of the swing increases

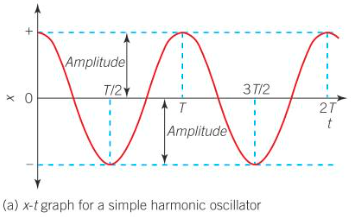
Displacement against Time period of SHM (released from amplitude)

Resembles cosine graph when released from amplitude

Resembles a sine graph when released from equilibrium

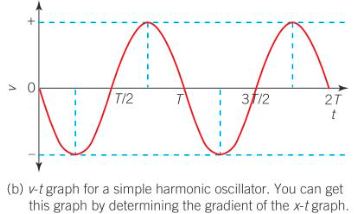
Velocity against Time period of SHM (released from amplitude)

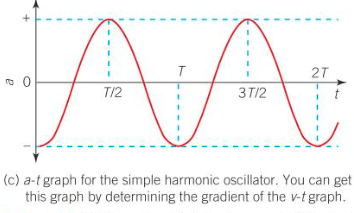
Acceleration against Time period of SHM (released from amplitude)

Velocity of SHM

v = ±ω√(A² - x²)

• ω = angular veocity (rad s^-1)

• A = ampliutude (m)

• x = displacement (m)

Max velocity of SHM

v_{max ⁼} ωA

• ω = angular velocity (rad s^-1)

• A = amplitude (m)

*obtained from v = ±ω√(A² - x²) when displacement is zero

• velocity is max when object has returned to equilibrium position

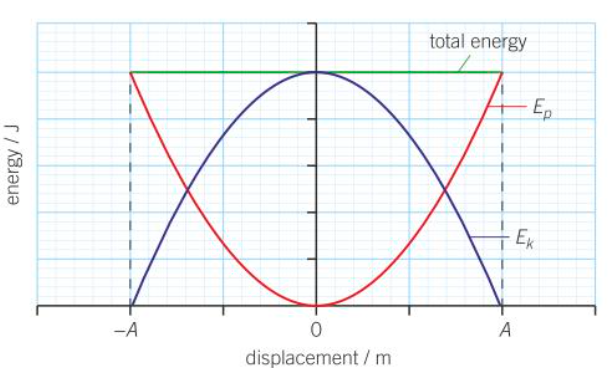
Energy against Displacement of SHM

Damping

When an external force acts on an oscillator, gradually reducing the amplitude of oscillations over time

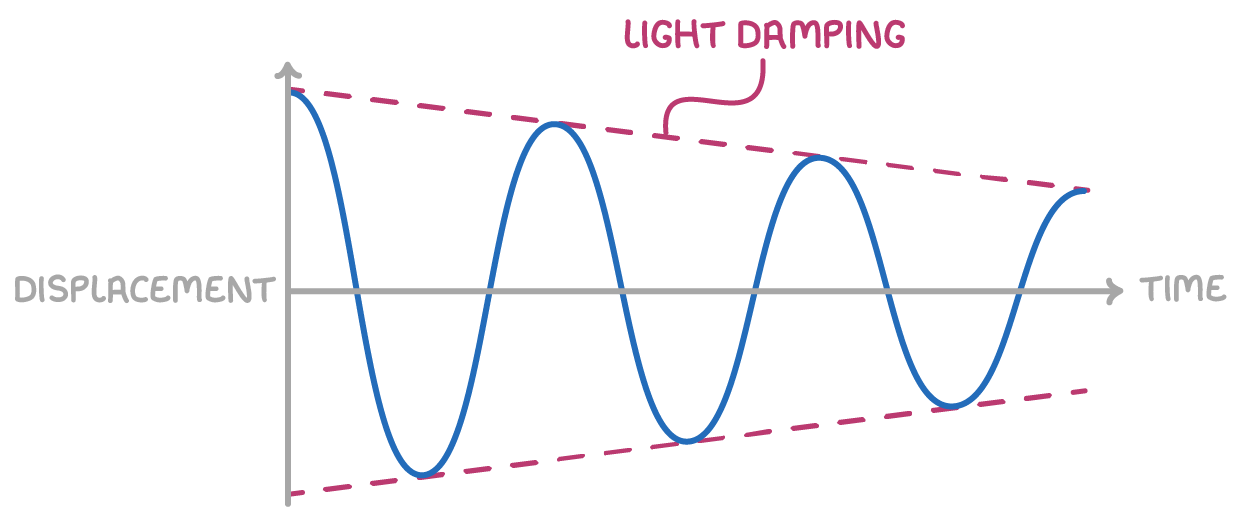
Light Damping

• Amplitude of oscillations decreases over time

• Period remains the same

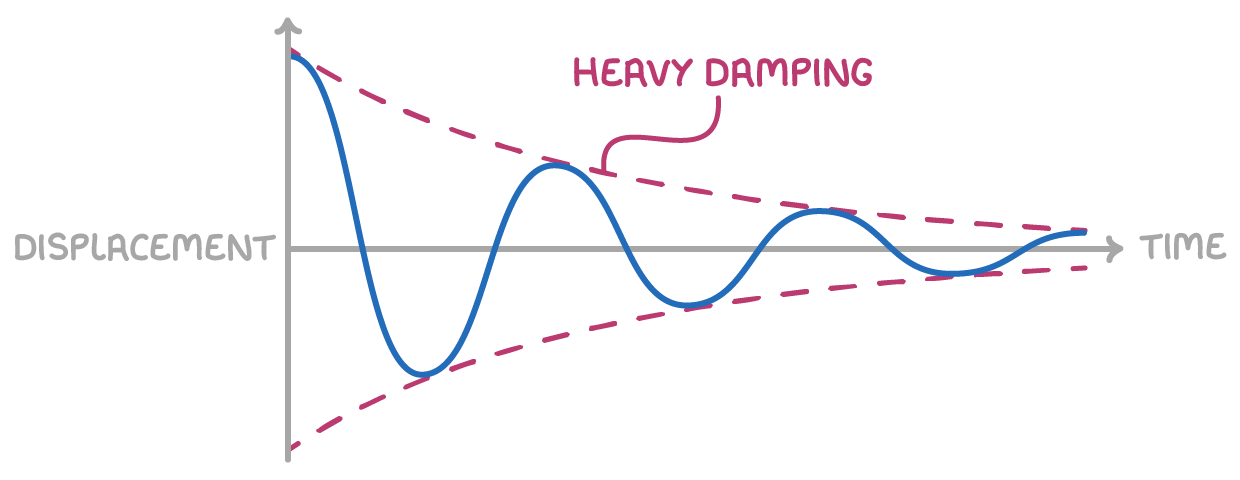
Heavy Damping

• Amplitude decreases significantly over time

• Period increases slightly

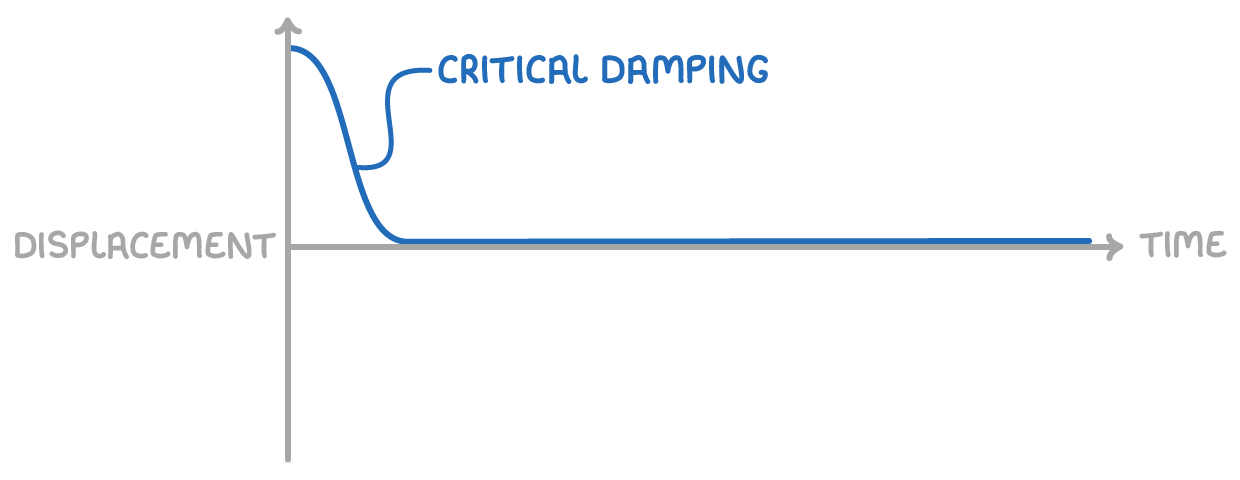
Very Heavy Damping

• No oscillatory motion

• Oscillator moves slowly to equilibrium position

Free Oscillations

When an object is allowed to oscillate without any external forces

Natural frequency

The frequency of a free oscillation

Forced Oscillation

When a periodic driving force is applied to an oscillator

E.g: vibration generator

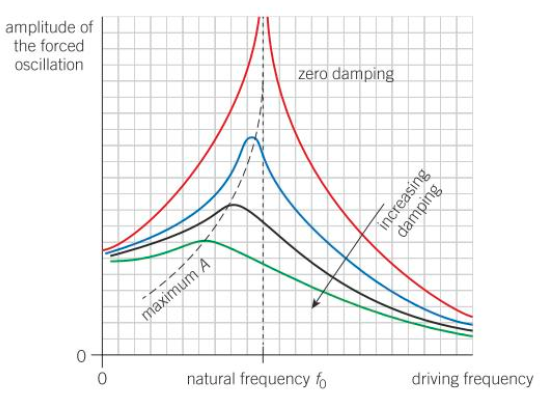
Resonance

Occurs when:

• Driving frequency = natural frequency

Results in the amplitude of oscillations increasing dramatically

Damping Forced oscillations

Has the effect of reducing the amplitude of oscillations

Degree of damping also affects frequency of driver at max amplitude

For light Damping:

• max amplitude at natural frequency of forced oscillator

As amount of damping increases:

• Amplitude of vibration at any frequency decreases

• Max amplitude occurs at lower frequency than f₀

• Peak n graph becomes flatter and broader