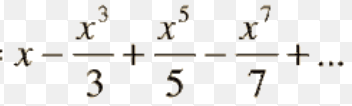MAT 021C memorization
0.0(0)
Card Sorting
1/25
There's no tags or description
Looks like no tags are added yet.
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
26 Terms
1
New cards
Sequence of Partial Sums
For a series ∑(n=1 to ∞) aₙ, the sequence {sₙ} where sₙ = a₁ + a₂ + ... + aₙ. If lim sₙ = S, the series converges to S; otherwise, it diverges.
2
New cards
nth Term Test for Divergence
If lim aₙ ≠ 0, the series diverges. If lim aₙ = 0, the test is inconclusive.
3
New cards
Geometric Series
∑(n=0 to ∞) arⁿ. Converges to a/(1−r) if |r|
4
New cards
Telescoping Series
∑(f(n) − f(n+1)). Partial sum sₙ = f(1) − f(n+1). Converges if lim f(n+1) exists.
5
New cards
Integral Test
If aₙ = f(n) (positive, decreasing), then ∑aₙ and ∫f(x)dx both converge or diverge.
6
New cards
p-Series
∑1/nᵖ. Converges if p>1; diverges if p≤1.
7
New cards
Direct Comparison Test
If 0 ≤ aₙ ≤ bₙ: ∑bₙ convergent ⇒ ∑aₙ convergent; ∑aₙ divergent ⇒ ∑bₙ divergent.
8
New cards
Limit Comparison Test
If lim(aₙ/bₙ) = c ∈ (0,∞), ∑aₙ and ∑bₙ behave alike. If c=0 and ∑bₙ converges, ∑aₙ converges.
9
New cards
Absolute Convergence
If ∑|aₙ| converges, then ∑aₙ converges absolutely (and thus converges).
10
New cards
Ratio Test
If lim|aₙ₊₁/aₙ| < 1, absolute convergence; >1, divergence; =1, inconclusive.
11
New cards
Root Test
If limⁿ√|aₙ| < 1, absolute convergence; >1, divergence; =1, inconclusive.
12
New cards
Alternating Series Test
For ∑(−1)ⁿaₙ (aₙ > 0): Converges if aₙ decreases and lim aₙ = 0.
13
New cards
Alternating p-Series
∑(−1)ⁿ⁺¹/nᵖ: p>1 ⇒ absolute conv.; 0
14
New cards
Term
Definition
15
New cards
Second Derivative Test
A method to classify critical points (a,b) of f(x,y) using the discriminant D = fₓₓ(a,b)⋅fᵧᵧ(a,b) − [fₓᵧ(a,b)]².
16
New cards
Discriminant (D)
The value D = fₓₓ⋅fᵧᵧ − (fₓᵧ)² used in the Second Derivative Test to determine the nature of a critical point.
17
New cards
Local Minimum
If D > 0 and fₓₓ(a,b) > 0 at a critical point (a,b), then f has a local minimum at (a,b).
18
New cards
Local Maximum
If D > 0 and fₓₓ(a,b) < 0 at a critical point (a,b), then f has a local maximum at (a,b).
19
New cards
Saddle Point
If D < 0 at a critical point (a,b), then f has a saddle point at (a,b).
20
New cards
Inconclusive Case
If D = 0, the Second Derivative Test fails, and other methods must be used to classify the critical point.
21
New cards
Taylor Series Expansion of e^x
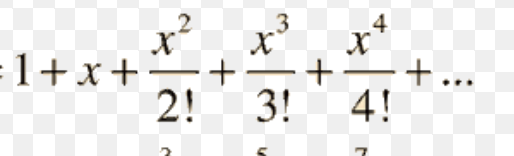
22
New cards
Taylor Series Expansion of sin x
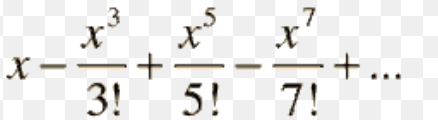
23
New cards
taylor series expansion of cos x
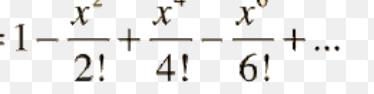
24
New cards
taylor series expansion of ln (1+x)
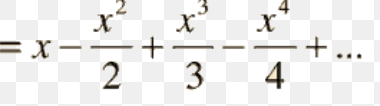
25
New cards
taylor of 1/1-x
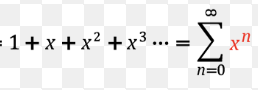
26
New cards
taylor of tan inverse