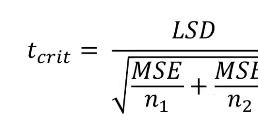Factorial ANOVA

What is a factorial ANOVA

A test with more than 1 independent variable

• Allow us to test for interactions

What is an interaction, main effect, simple effect

Interaction: - Examining if the effect of IV1 on the DV depends on the level of IV2 on DV (Level of A depends on B)

Main effect: overall effect of one variable - A main effect tests whether means differ across levels of one factor while collapsing across the other factor.

Simple effect: effect of that variable within one specific level of the other variable

Factors vs levels

Independent Variable

EG: Experiment to look at the effects of drug a vs drug b (assigned to 10mg, 20mg, 30mg)

• Drug a and b would be the factors

• Mg would be the 3 levels

What levels are compared in a factorial design?

Every level of every factor is paired with every level of every other factor (all combinations are included) 

Eg: each person will have some level of drug b and drug a (12 different variations) 

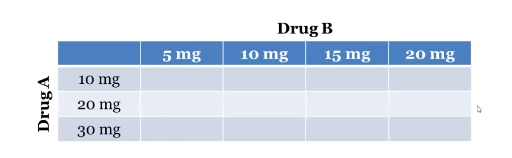
What kind of factorial design is this 

Tow factor - 3×4 factorial design representing the number of levels

• Factor with 3 levels fully crossed with a factor of 4 levels 

What does it mean to have a between-subjects design in this context

Different participants in each cell (only one level of drug a and one level of drug b)

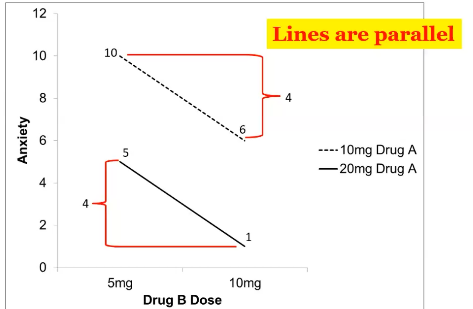
What does no interaction look like?

If the lines are parallel - EG: drug B dose and anxiety 

• As the dose increases by 4 on both drugs (the effect of drug b did not depend on the level of drug a) 

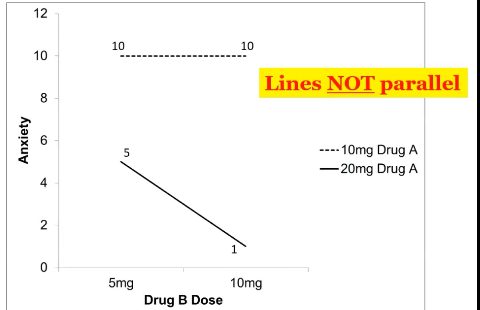
What does it look like when there is an interaction

Lines are not parallel - if you extended them out they would eventually cross 

• Effect of drug b depends on the effect of drug a - the change as we change from one condition to another depends on what is going on with the other 

What does the source table look like?

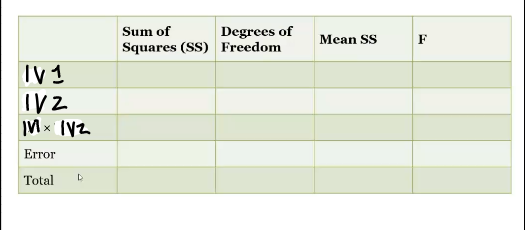
Different df

Group = k (levels) -1

Interaction = product of group df (group 1 df = group d df) 

Error = df total - group and interaction terms (N - # of cells) 

Total = N (total people in expirement) -1 

ss total

look at each individual person and subtract their mean from the grand mean

SS group

 Sum of: n_j (x hat - x hat)²  on each side

• (but them under each iv ss)

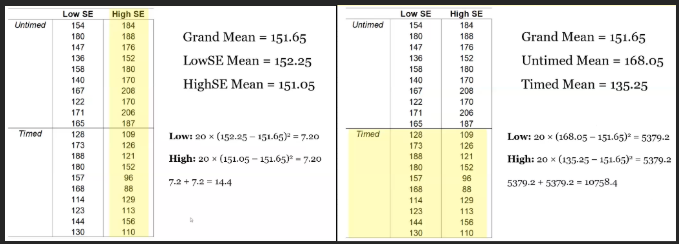
SS interaction

Have to compute ss cells ]

• Compute the mean of each cell 

• Subtract this mean from the grand mean 

SS _IV¹xIV² = SS_cells - SS_IV¹ - SS_IV²

What is ss cells

Only a step of calqulating ss intercation, not the same thing

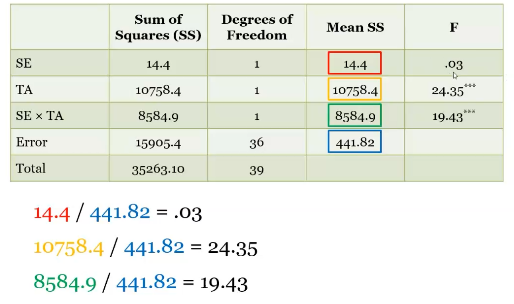
Mean SS and F 

Mean ss: Divide Across 

F: Divide each ss by the error term

Main Effects VS Simple effects

Main: The effect of one if the IVs averaged across the levels of the other IV

• Imagine you’re looking at whether sleep affects test scores - You also have a second variable, caffeine, but you’re not thinking about it right now.

• A main effect of sleep asks: “On average, does more sleep lead to higher scores?”

Simple: The effect of one of the IVs at one level of another IV - testing the little space

• “Within high caffeine, does more sleep improve scores?”

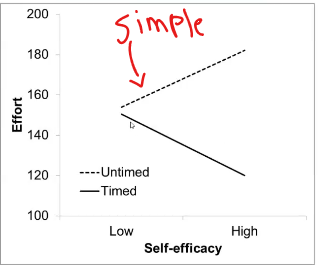
What does it mean when you find a significant effect 

Means theres an interaction (lines arent horizontal) 

• We have to do a test to see if there is actually an interaction 

• Is the deviation from parallel significant 

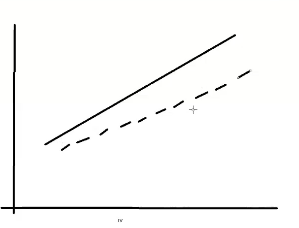
How to calculate simple effects (using MSE)

Use MSE and a new source table 

*df and mean mse directly from omnibus table

How to calculate simple effects (using t-test)

(do the same with the high end)

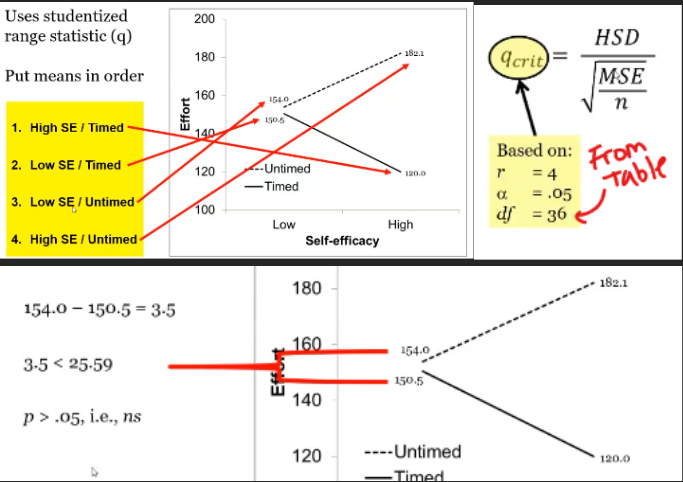
Calculate simple effects using Tukey

1. Put means in order

2. Calculate r= (largest position - smallest position) +1

3. Find q-crit 

4. Compare each difference (is it sig) 

ada² and partial ada²

Calculating Effect sizes

• Ada² will always be smaller than partial ada²

• partial ada² prefered bc it isolates variance for just that factor 

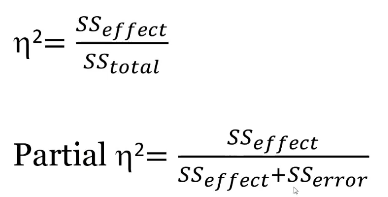
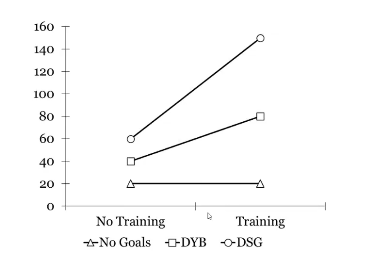
What is this an example of?

(two main effects and an interaction)

• effects of training tends to depend on what type of goals you set

• Strong effect on top and no effect on bottom

Calculating simple effects

SS = N (mean - mm)²

What happens when you have significant fs → don’t know which are significant (which are different from eachother) 

You use a t-test as a follow up (with three means)