Economics 2: Consumer Theory

Reflexivity Assumption

• It is assumed that each bundle is at least as good as itself

Preference Symbols

Ad valorem tax and subsidy

• Ad valorem means 'to add value'

• An ad valorem tax means a tax is paid on a good based on its price; a subsidy implies the inverse

Budget Constraint

• The budget line is given by p₁x₁ + p₂x₂ = m, which just exhausts a persons income

• It has a slope of −⁡p₁/p₂, a vertical intercept of m/p₂, and a horizontal intercept of m/p₁.

• The Numeraire is when one of the variables is fixed as constant; this doesn't change the constraint (check by rearranging)

• Increasing income shifts the budget line outward. Increasing the price of good 1 makes the budget line steeper. Increasing the price of good 2 makes the budget line flatter.

Pareto Efficiency

• An allocation is Pareto Efficient if there is no way of making one better off without making another worse off

Equilibrium Principle

• Generally, prices are determined when supply for a good meets the demand for a good

Optimisation Principle

• People choose the best patterns of consumption available to them 

Endogenous and Exogenous Meaning

• Most simply, endogenous variables are explained and contained in a particular model whereas exogenous variables are not 

Marginal Rate of Substitution

• The rate at which an agent will swap one good for another

• The slope of an indifference curve

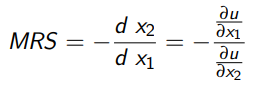
Monotonic Transformation

• Utility functions are ordinal, meaning they only show an order of preference, but don't assign an actual value to preferences

• If preferences are represented by numbers - coffee = 4 and tea = 5 - by adding 5 to the values the order of preference is preserved

Perfect Substitutes

• An agent is completely indifferent between two goods; they seek to maximise utility regardless of which good they have 

• u(x,y) = x + y

Perfect Complements

• When two goods are only enjoyed when consumed together; there is no point having more of one good without the other

• u(x,y) = min(x,y)

Convexity Assumption

• Averages are better than extremes

• This works when we take a weighted average of two bundles of goods and represent it on an indifference curve; this new curve will be equal to or strictly preferred to the singular curves

Transitivity Assumption

• A logical assumption which mitigates against preference cycles

• There is no situation in which A > B, B > C, and C > A

Monotonicity Assumption

• Assumes that more of a good is better

• This simply means that in models we will only study allocations of goods before satiation occurs

Completeness Assumption

• Agents are able to exhibit preferences, avoiding situations in which they can't choose between different bundles

Marshallian Demand

• The solution to the constrained optimisation problem in the image 

• This solution gives the optimum quantity given fixed income and prices x(p,m)

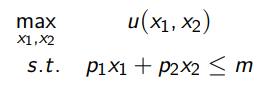
The Equimarginal Principle

• Most utility curves are smooth and convex (Cobb-Douglas Equations)

• At the optimum, the indifference curve and budget constraint will be tangent at the optimum, giving the equimarginal condition

• Find the marginal utility by differentiating a utility function with respect to one of the arguments, then set the ratio of the marginal utilities equal to the ratio of the prices

• MU_x1/MU_x2 = x₂/x₁, x₂/x₁ = p₁/p₂

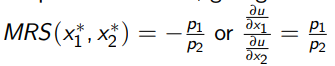
The Lagrange Method

Revealed Preference

• In a situation where there are two goods available and one chooses A over B, we can say that A is revealed preferred to B 

Weak Axiom of Revealed Preference

• If a person chooses x over y at some prices p when both are affordable, we can never reverse the choice at any other price in which both are affordable

• Thus, something consists with the weak axiom of revealed preference if someone has a strict preference of one good over another

Strong Axiom of Revealed Preference

• Adds a condition to the weak axiom which ensures that transitivity is respected

• If A is revealed preferred to B, and B is revealed preferred to C, then C can not be revealed preferred to A (this event would be lots of curves crossing each other)

Optimal choices for concave preferences

• Concave preferences imply a person doesn’t want to buy two goods together (like olives and ice cream; if they have ice cream they DON'T want more olives)

• Thus the solution for nonconvex preferences is always a boundary point

Shortcut for optimal choices in Cobb-Douglas

• To be used instead of conducting the Lagrangian, where the Cobb-Douglas is given by u(x₁,x₂) = x₁^cx₂^d

• It is often useful to choose Cobb-Douglas functions where the exponents sum to 1 because this means that the exponents can be interpreted as a fraction of income

Normal good

• A type of good where an increase in income will increase demand (eg cars, steaks)

• dx₁*/dm > 0

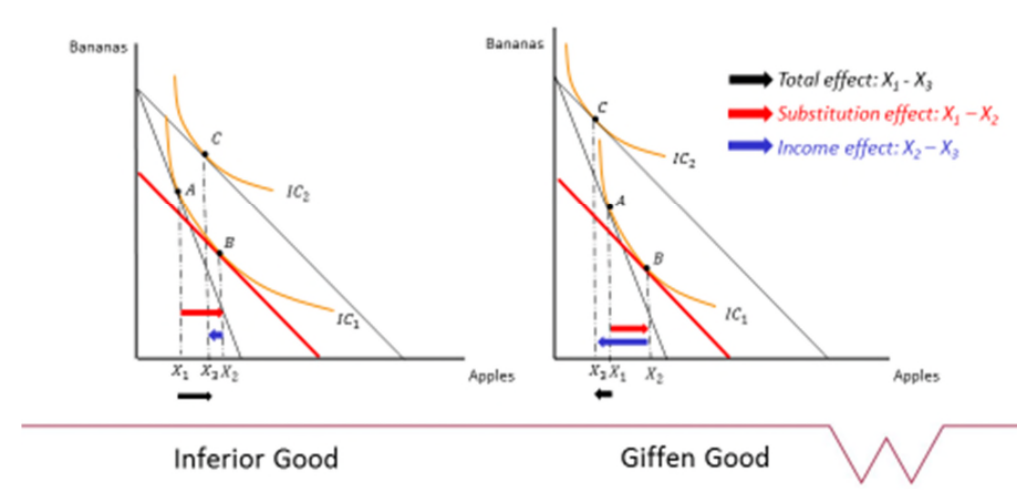
Inferior good

• As income increase, demand for the good decreases (eg fast food)

• dx₁*/dm < 0 

Ordinary good

• Demand decreases when price increases (eg clothes)

• dx₁*/dp₁ < 0

Giffen good

• Demand increases when the price increases (watches, cars)

• Often referred to as luxury goods; they are partly valued because of their price

• dx₁*/dp₁ > 0

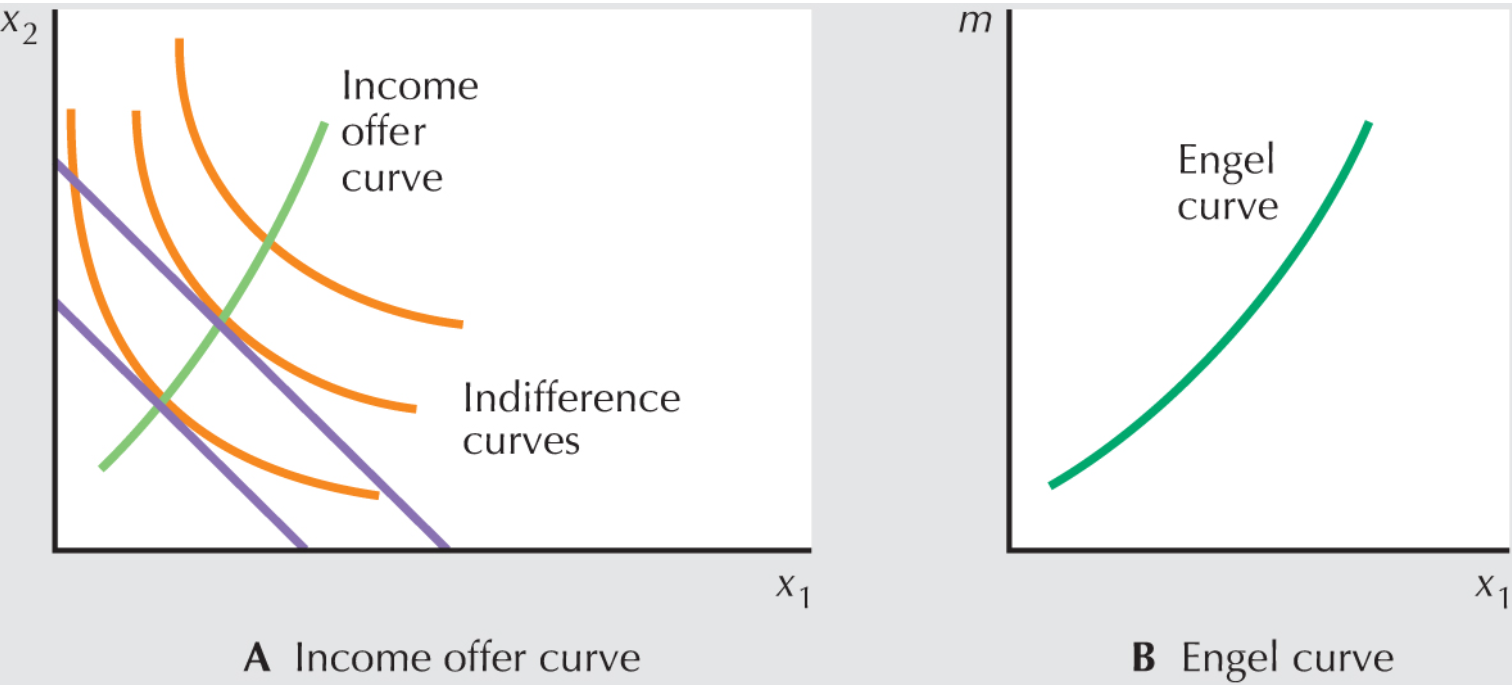
Engel Curve and Income Offer Curves

• The shape of the income-offer curve is referred to as the income-expansion path; when income increases and the goods are normal, the slope will be positive 

• The income offer curve illustrates the bundles of goods demanded at different income levels 

• The Engel curve is one which shows the path of demand for a good given fixed prices

Demand Curve

• Derived by plotting all of the price-demand combinations on a graph (price over demand)

• Shows how one person reacts to changes in price and income

Price Elasticity of Demand

• The slope of a demand function, understood as the ratio of relative changes

• When the PED > 1, demand is called elastic, meaning that the demand curve is flatter (x changes a lot with price)

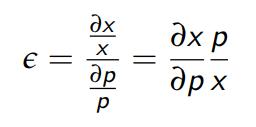
Constructing market demand

• Summing horizontally is equivalent to fixing the price and summing the demand of different consumers

• This allows one to find aggregate market demand at a particular price

• Kinks can occur when one is summating market demand and a price goes above one of the consumers WTP

Slutsky Decomposition

• Deals with the effects a price change has on demand

• The first effect is the substitution effect; a person switches consumption to the other good

• The second effect (income effect) involves a loss of purchasing power

• This separating of these two effects is called the Slutsky decomposition

Compensated Demand 

• Is constructed to eliminate any purchasing power effect 

• If original prices are p₁ and p₂, with income m, then when prices change to p₁’ and p₂, the new income must be m’ to allow for purchasing the same quantities at different prices 

Substitution effect

• When a person shifts consumption from one good to another after a price change

• The difference between the bundle x* and x’ (where x* is the original quantity demanded, and x’ is the quantity demanded after the price change)

• The solution to max_(x1,x2) u(x₁,x₂) s.t. p₁’x₁ + p_2×2 = m’

Income effect

• The loss of purchasing power caused by a price change, which is found by locating the optimal bundle at a new price and non-adjusted income

• We move from x’ (adjusted demand with adjusted income) to x’’ (adjusted demand with non-adjusted income)

• The income effect is the difference between x’’ and x’

• The solution to max_(x1,x2) u(x₁,x₂) s.t. p₁’x₁ + p_2×2 = m

• Graphically, this is a linear transformation of the budget constraint and indifference curve tangency 

Slutsky Decomposition - Maths

• Where dx/dp is the change in demand w.r.t the change in price and x*(dx/dm) is the income effect

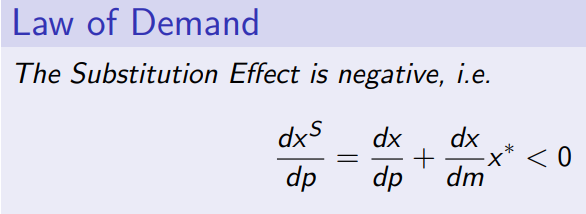
Homothetic preferences on Engel and Income Offer curves

• They will always be represented as straight lines through the origin, because any change in the quantity of bundles doesn’t change the ratio of preferences

Quasilinear indifference curves

• All the indifference curves are just linear transformations of one indifference curve 

• We say that there is zero income effect due to an increase in income, and the Engel’s curve is a straight vertical line 

The Price Offer Curve

• When we change the price of one good, keeping the other fixed, the budget constraint pivots, intersecting different indifference curves at different points

• These new intersections are connected through the price offer curve

Hicksian Compensated Demand

• Also known as the Hicksian Subsitution Effect, this computes the optimal point by fixing utility and finding the compensated demand required to reach this utility

• This implies a new solution framework; we can’t maximise the problem because we’re keeping utility fixed, so we invert it and solve in terms of expenditure minimisation instead

• We minimise expenditure using the Lagrangian or Equimarginal Principle

• min_x1,x2 p₁x₁ + p₂x₂ , s.t. u(x_1,x₂) = u*, where u* is the fixed level of utility

• The minimal point lies on the lowest budget line touching the indifference curve constraint 

Unconstrained Optimisation 

• Rearrange the budget constraint to get x2 = (m-p₁x₁)/p₂

• Substitute this into the utility expression and then maximise it, solving for x₁ by setting it equal to 0

Hicksian Demand Substitution Effect

• We want to fix utility at its optimal level, so plug the Marshallian demands into u(x₁, x₂) to find the optimal utility, u*

• Minimise expenditure subject to the new constraint (ie, x₁x₂ = u*) and compute 

• Solve for new optimal quantities given the price changes; take x₂ from x₂^* to see the substitution effect 

• These new optimal quantities, x₁^* and x₂^* are called Hicksian Compensated Demands, subject to H(P1, P2, v), where v is the fixed level of utility 

Hicksian Demand Income Effect

• Simple compute the Marshallian demands of the goods at the new prices; this accounts for what expenditure will actually be like given the change in income 

Hicksian Demand Total Effect

• The direction of the total effect depends on what type of good it is; for a normal good, the substitution and income effect will both be positive

Compensating Variation

• Fix utility before the price change and find how to adjust income to ensure the same utility after the price change

• If e(p’, u(x*(p, m))) is the minimum expenditure needed to achieve the same utility at final prices, then the compensating variation, CV (p,p’,m) = |m - e(p’, u(x*(p, m)))|

Equivalent Variation 

• Fix utility after the price change, u(x*(p’, m))

• Tries to figure out how we can adjust the income to ensure the consumer experiences the same level of utility before the price change as it does after 

• EV(p, p′, m) = |e(p,u(x*(p′, m))) − m|

Consumer Surplus

• The net benefit we receive from consuming q units of good 1, where CS(q₁) = v(q₁) - p₁q₁

• The area below the demand curve

Comparing Equivalent Variation and Compensated Variation

• For a normal good, CV > EV for a price increase and vice versa for a decrease

• They will only be equal for quasilinear preferences where indifference curves are parallel and there is no income effect

Computing Compensated Variation

• Original budget constraint is P₁*x₁* + P₂x₂ = E₁. When the price of P₁ rises to P₁**, the budget constraint changes with new Marshallian Demands to become P₁**x₁** + P₂×₂** = E₁

• We shift the second budget line out so that it becomes tangential to the original utility curve. The budget constraint becomes E₂ = P₁**x₁*** + P₂x₂*** where E₂ is compensated income

• E₂ - E₁ is the compensated variation

Computing Equivalent Variation

• How much money to take away from a consumer before a price change to ensure they will be just as well-off after it

• Original BC is P1*x1* + P2x2* = M1

• When the price P1 rises, BC pivots inwards and new BC is P1**x1** + P2x2** = M1

• We must takeaway money from the consumer to ensure constant utility, so shift the original BC inwards to get the new BC P1*x1*** + P2x2*** = M2

• EV = M1 - M2