1 - Factorial design

What is a factorial design?

It's a design that includes multiple independent variables

An example of a factorial design

A study looking at exam performance based on caffeine and time may have two factors:

=Coffee vs no coffee (two levels)

=morning vs noon vs night (multiple levels)

Factor or independent variable?

The two terms are interchangeable meaning the same thing

What does the name of an experimental design depend on?

-Number of IVs

-Number of levels in the IVs

-Type of IV used

An example of experimental design name based on the number of IVs

-One IV = one-way design

e.g., does coffee influence exam scores

-Two IVs = two-way design

e.g., does time of day or coffee influence exam scores?

-three IVs = three-way design

e.g., does time of day, coffee drinking or age influence exam scores?

An example of experimental design name based on number of IVs

-Can be between-groups, within-subjects or mixed design

-If we treat caffeine and time as two between-groups variables, we would have a 2x3 two-way, between-groups design

What do you want to know in a factorial design?

(And calculate F for)

-The effects of each individual variable (main effect)

e.g., wanting to know if drink type has an effect on exam scores independent of anything else

-The effects of two or more variables when considered together (interaction effect)

What are the stages of two-way between groups ANOVA?

-Same as one-way

=State null hypothesis (H_0) -> Partition the variability -> Calculate mean squares -> calculate F-ratios

What are the null hypothesis you need to state in a factorial design?

-Need to specify at least three H0 = each null hypothesis for the two main effects of the IV

1. Means of different levels of IV A are the same

=𝜇A1 = 𝜇A2

2. Means of different levels of IV B are the same

=𝜇B1 = 𝜇B2

3. Difference between means of B are different at different levels of A (there is no interaction between two variables)

=𝜇A1B1 - 𝜇A1B2 = 𝜇A2B1 - 𝜇A2B2

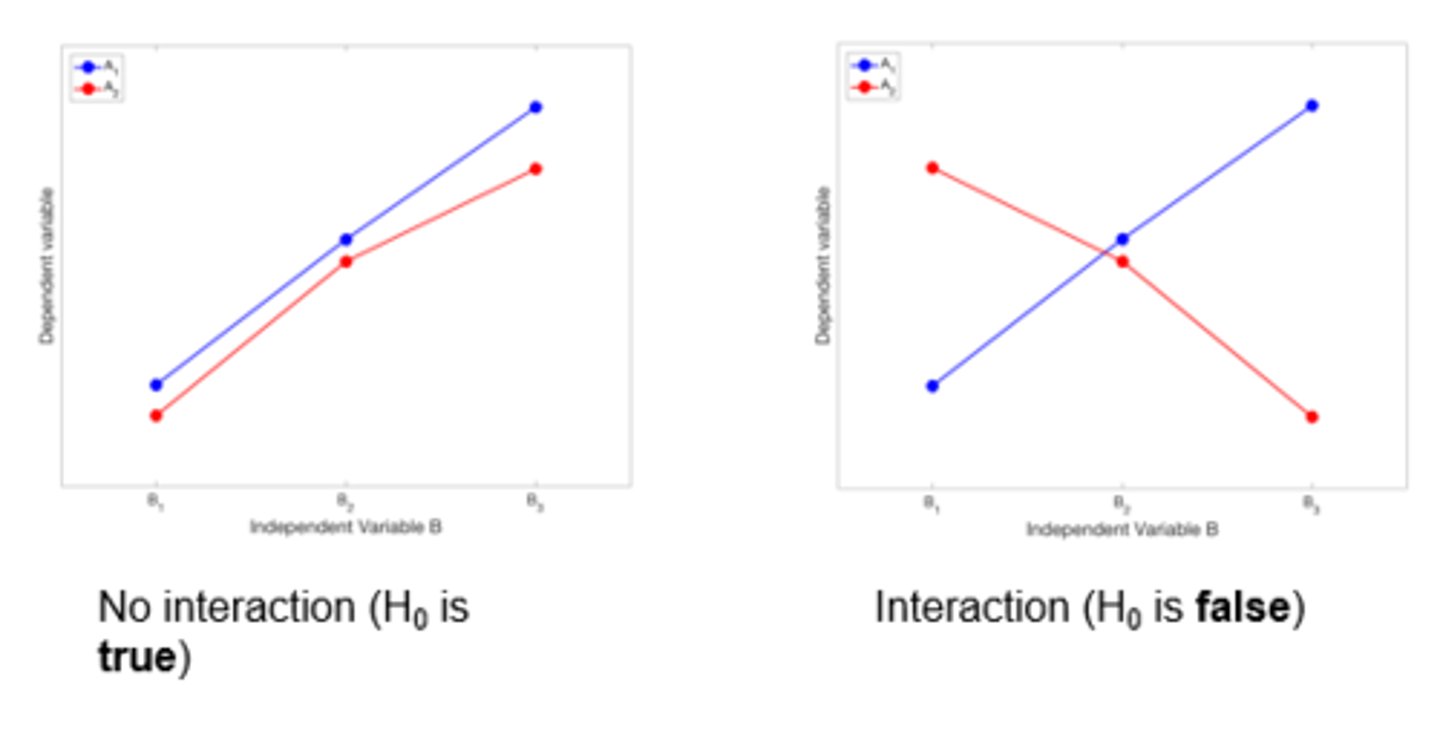
A visual example of no interaction vs interaction

1. For IV A, as the IV changes the difference between the two levels of IV A are the same

2. Differences in direction in factor A depending on different levels of factor B

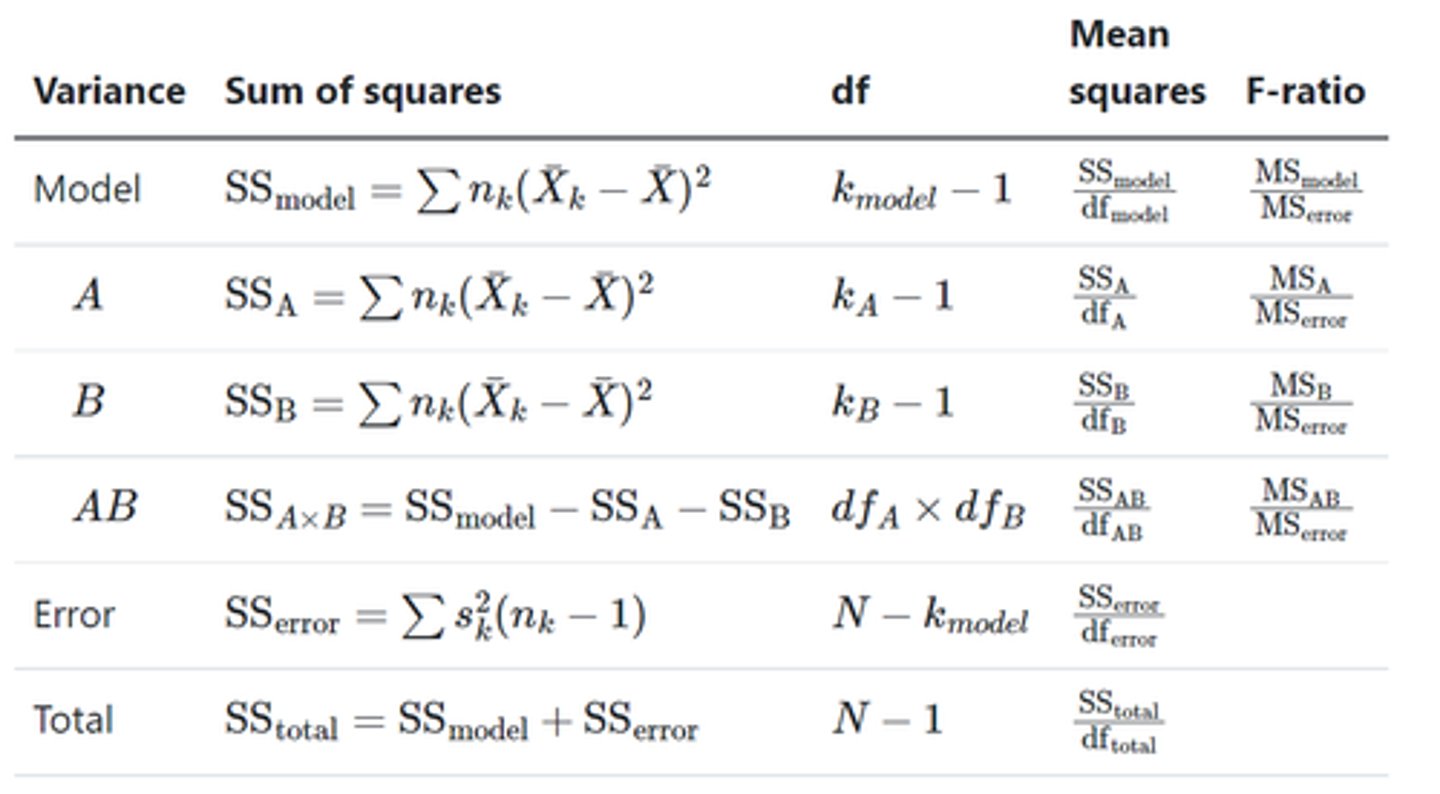
What is the partitioning variability process?

Total Variability (SS_T) -> Variability explained by the experiment (SS_M) and Unexplained variability (SS_R) -> Variability explained by Variable A (SS_A) + Explained by B (SS_B) + Explained by an AxB interaction (SS_AxB)

-Looking at the contributions of each and then compare to our unexplained variability or error to see if there is a significant impact of each main effect interaction

What is the total sum of squares (SS_T)?

-Variability of all scores in a dataset (regardless of group assignment)

=Calculate grand mean (mean of all our data in the dataset) to then work out Sum of squares)

What is total variability explained by the experiment (SS_M)?

Variability in the model that can be explained by the experiment

How to calculate total variability explained by the experiment (SS_M)?

-For each group (regardless of factor):

=Subtract the group mean from the grand mean, and square this

=Multiply this by the number of participants in the group

=Add all values together to calculate SS_M

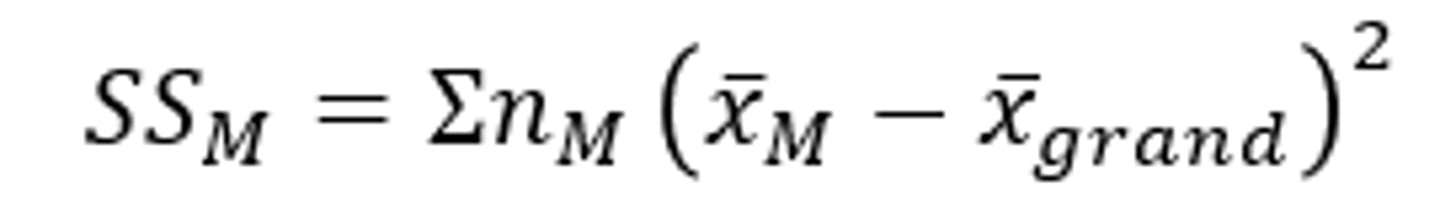
How to calculate variability explained by the experiment (SS_A and SS_B)?

-For main effects of factors A and B:

=for each level of factor:

=Subtract the group mean from the grand mean and square this

=Multiply this by number of participants in the group

=Add all factor level together to calculate SS

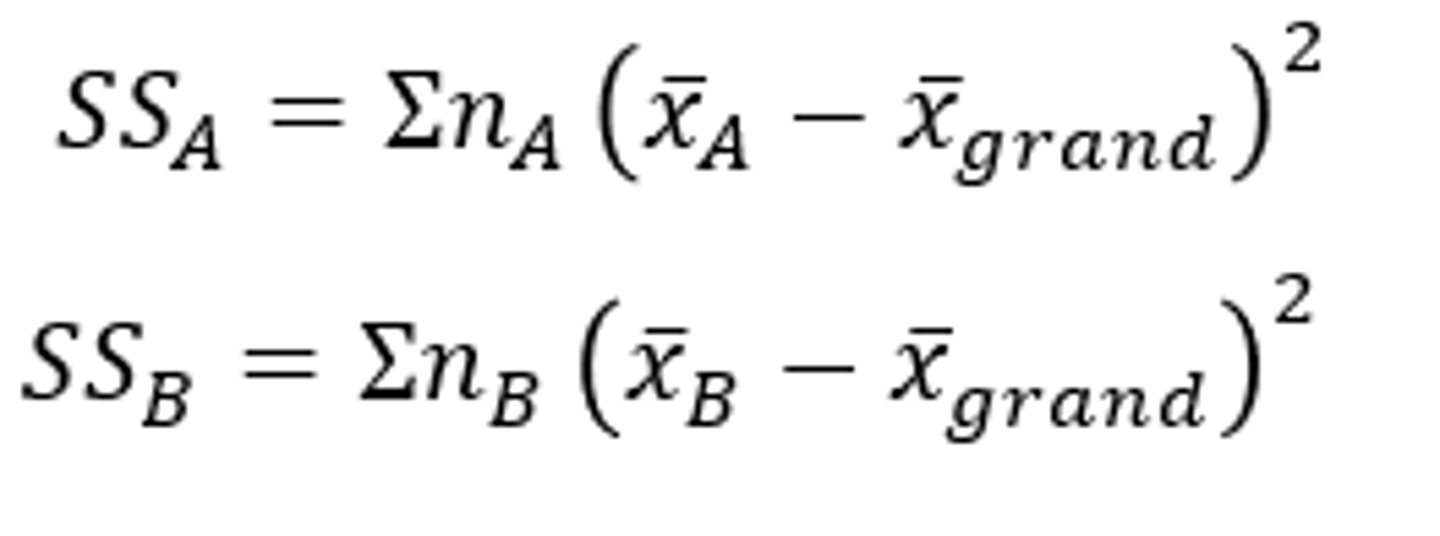
How to calculate the interaction (SS_AXB)?

-After calculating three equations (SS_M, SS_A, SS_B)

=Subtract SS_A and SS_B from SS_M

-The total amount of variability explained by the interaction between variables A and B

How to calculate variability not explained by the experiment?

-If you know SS_T and SS_M, you can easily calculate SS_R

=SS_R = SS_T - SS_M

How to calculate the mean squares for factorial ANOVA?

-Need to calculate mean squares for main effects, the interaction, and the error term

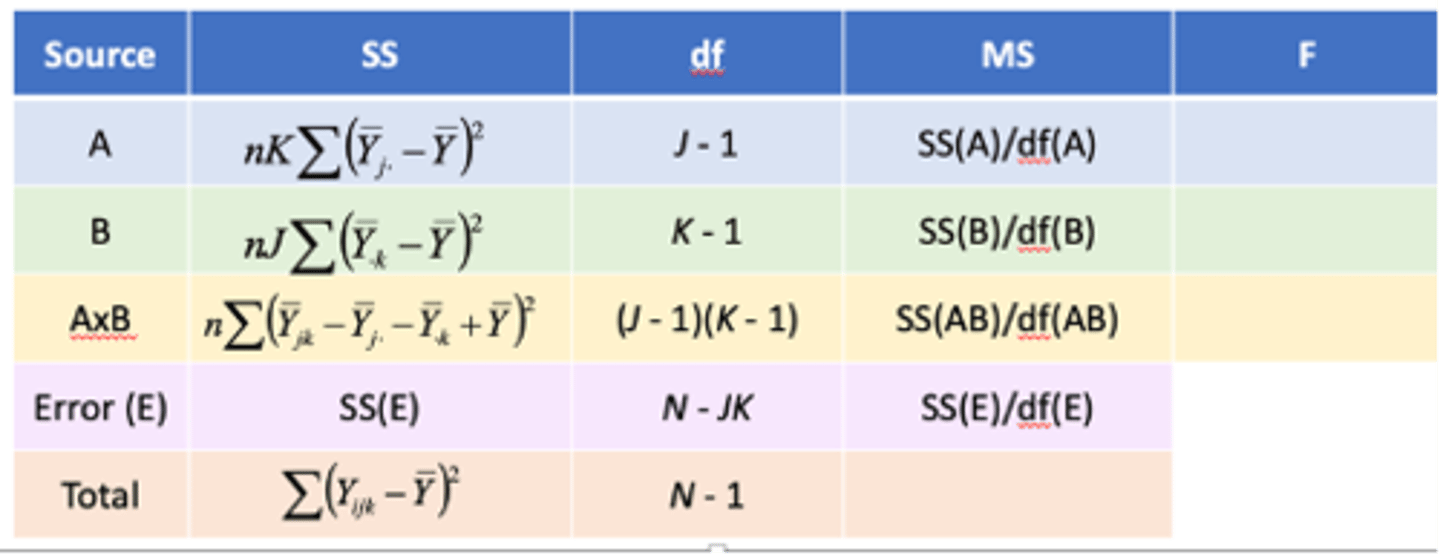
How to calculate the f-ratio for factorial ANOVA?

-Calculate f-ratios for main effects and interactions by dividing their mean squares by our mean square error

=MS_A;B;AB/ MS_R

How to evaluate f-ratios?

-Use critical values table to evaluate if our main effects and interaction are significant

e.g.,

-Main effect of coffee = •Our critical F value is 4.26. Because our observed F (9.45) is bigger than this, we have a significant main effect of coffee intake at p<.05 (df at 1,24)

-•Main effect of time of day = •Our critical F value is 3.4. Because our observed F (0.41) is smaller than this, we have a nonsignificant main effect of time of day at p<.05) (df at 2,24

-•Interaction between coffee and time of day

=•Our critical F value is 3.4. Because our observed F (7.12) is bigger than this, we have a significant interaction between coffee intake and time of day at p<.05. (df at 2,24)

Example of writing out factorial ANOVA (2x3) results for main effects

Main effect of drink type: There was a significant main effect of drink type on exam scores [F(1,24)= 9.35, MSE= 2.6, p=.005, np2= .28]. Participants who drank water had lower exam scores (m=4.87) than participants who drank coffee (m=6.67)

Main effect of time of day: There was no significant main effect of time of day on exam scores[F(2,24)= 0.4, MSE= 2.6, p=.676, np2= .032]

Example of writing out factorial ANOVA (2x3) results for interaction

Drink type x time of day interaction: There was a significant interaction between drink type and time of day on exam scores [F(1,24)= 9.35, MSE= 2.6, p=.004, np2= .37].

What is simple main effects?

-An analysis comparing the effects of one IV at different levels of the second IV - to know what our interaction term means

How to report a simple main effect?

e.g., What impact does drink type have on exam score at different times of the day?

There were no significant effects of drink type when exams were taken in the morning (p=.337) or the afternoon (p=.062). However, there was a significant effect of drink type in the evening [F(1, 24)= 18.62, MSE= 2.6, p<.001, np2= .437). When participants took an exam in the evening, scores were higher for participants who drank coffee (m= 8.2) than for participants who drank water (m=3.8).