(y1 only) sequences and series whole topic

sequence

a list of items e.x. 1, 2, 3 ...

series

the sum of a list of terms e.x. 1 + 2 + 3...

sequence and series definitions

increasing and decreasing- each term is greater/lesser than the previous

periodic- the terms repeat in a cycle (u^(n + k) = u^n with an order of k (k unique terms that repeat))

arithmetic sequences

sequences with a common difference between each term

e.x. a, a + d, a + 2d

the nth term is given by u^n = a + (n - 1)d

arithmetic series

sum of the terms of an arithmetic sequence

given by s^n = (n/2)(2a + (n - 1)d) or s^n = (n/2)(a + l)

where n is the number of terms, a is the first term, d is the common difference and l is the last term

proving arithmetic serieses

S^n = a + (a + d) + (a + 2d) ... (a + (n - 2)d) + (a + (n - 1)d)

S^n = (a + (n - 1)d) + (a + (n - 2)d) ... (a + 2d) + (a + d) + a

2S^n = n(2a + (n - 1)d)

therefore S^n = (n/2)(2a + (n - 1)d)

geometric sequences

sequences where each term is r times the last

a, ar, ar^2, ar^3 ...

r is the common ratio

geometric sequence equation

the nth term is given by u^n = ar^(n - 1)

also, u^(k + 1)/u^k = u^(k + 2)/u^(k + 1) = r (pick any two pairs of adjacent terms, and the bigger divided by the smaller is the same for each)

geometric series

the sum of the terms of a geometric sequence

s^n = a(1 - r^n)/(1 - r)

also, by multiplying each side by -1:

s^n = a(r^n - 1)/(r - 1)

(invalid when r = 1 as division by zero)

proving geometric series equation

S^n = a + ar ... ar^(n - 1)

rS^n = ar + ar^2 ... ar^n

S^n - rS^n = a - ar^n

S^n(1 - r) = a(1 - r^n)

therefore S^n = a(1 - r^n)/(1 - r)

convergent and divergent sequences

sequences where the terms tend to a fixed limit or to infinity

convergent and divergent series

series where the sum tends to a fixed limit or to infinity

sum to infinity

the sum of the first n terms for geometric sequences as n approaches infinity

S^inf = a/(1 - r) (only works for convergent sequences, divergent sequences give infinity)

recurrence relations

a way of defining a sequence where each term is given as a function of the previous

e.x. u^(n + 1) = 2u^(n) + 4

sigma notation

∑- denotes the sum of a series

the number below denotes the first value of r and the number above denotes the last, and the equation to the right denotes the equation applied to r

binomial expansion

the process of expanding (a+b)^n expressions

pascal’s triangle

used to help binomial expansion- the (n+1)th row gives the coefficients in the expansion of (a+b)^n

formed by adding adjacent pairs of numbers to find the numbers on the next row

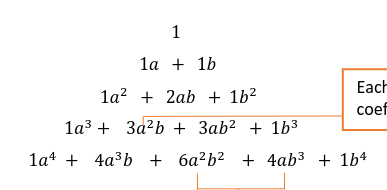
factorial notation

n! used to help binomial expansion, quicker than Pascal's Triangle for larger indices

nCr

nCr = n!/r!(n-r)!

gives the coefficient for the rth term for (kx+c)^n

the rth entry in the nth row of pascal's triangle is given by (n-1)C(r-1)

binomial expansion

a rule allowing for the quick expansion of brackets e.x.

(a+b)^n = a^n + (nC1)a^(n-1)b + (nC2)a(n-2)b^2 ...

finding coefficiencts

the coefficient of x^n in the binomial expansion (kx + c)^m is:

(mCn)(k^n)(c^(m-n))

binomial estimation

when x is less than 1, larger powers can be ignored to produce an estimation of the value of a binomial expression as their value will be negligible. the amount of terms to include in the estimation will be provided