Physics Year 1 Equations

1 mile

1600m

1 tonne

1000kg

Absolute uncertainty

Range/2

Percentage uncertainty

(Absolute uncertainty x 100)/mean value

Uncertainty of addition/subtraction

Add absolute uncertainties

Uncertainties of multiplication/division

Add %uncertainties and use result to find absolute

Uncertainties of raising to a power of n

Multiply %uncertainty by n

%uncertainty of gradient

(Best gradient-worst gradient)x100/best gradient

%uncertainty in y-intercept

(Best y-int. - worst y-int.)x100/ best y-int.

Typical walking speed estimate

1m/s

Typical running speed

5m/s

Typical cycling speed

7m/s

Typical car speed

20m/s

Typical train speed

50m/s

Typical height of person

1.8m

Typical mass of car

1000kg

Atoms in 1g

6.022×10²³

Speed v

Change in displacement s / time taken t

Acceleration a

Change in velocity v / time taken t

Area under velocity time graph

Displacement

Area under velocity time graph

Change in velocity

Suvat: s

s = ut + 0.5at²

Suvat: v²

v² = 2as + u²

Suvat: a

a = (v-u)/t

Suvat: s

0.5(v+u)t

Suvat: s

vt - 0.5at²

Suvat proof

Thinking distance

Speed x reaction time

Braking distance

-u²/2a

Stopping distance

Thinking distance + braking distance

Weight

mg(9.81)

Stopping distance and velocity relationship

d directly proportional to v²

Drag force and velocity relationship

Drag force is directly proportional to v²

Drag force and cross-sectional area relationship

Drag force is directly proportional to area

EXTRA: drag force equation with drag coefficient

0.5 x density x v² x drag coefficient x A

Acceleration due to drag force

• a = F/m

• a = (W-drag force)/m

• a = (mg - drag force)/m

• a = g - (drag force/m) < g

Moment M

Force, F x perpendicular distance of line of force of action to pivot, x

Torque of couple

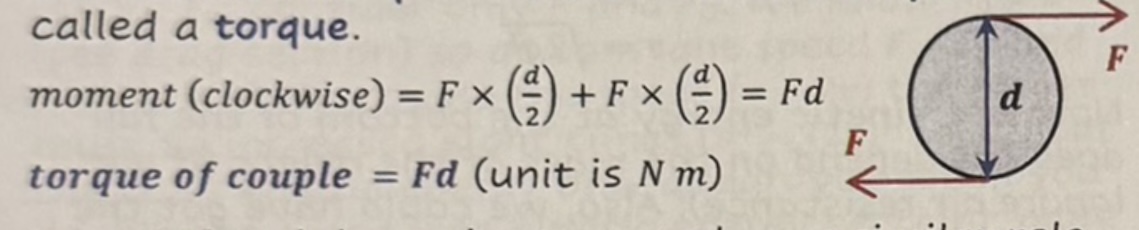
Density p

Mass / Volume

Pressure P

Normal force / Area

Pressure at depth h from height of liquid column

hpg (depth x density x gravity)

Upthrust

Upthrust = pVg (Upthrust = weight of object)

Work done WD

Force F x distance moved in direction of force x

Area under force-distance graph

Work done

KE

0.5mv²

Derivation of KE

• Object accelerates from rest to velocity v

• From suvat, v² = 2as + u², s = v²/2a

• W.D is Fs, so KE=Fs, so KE = ma x v²/2a = 0.5mv²

GPE

mgh

Power

W.D/t

Power, force, velocity equation derivation

• ONLY USE WHEN FORCE NEEDED TO MAINTAIN CONSTANT SPEED

• P=WD/t

• = Fx/t

• = Fv

Relationship between P and v

Since drag force is directly proportional to v² and at constant speed, F=drag force and so P= drag force x v, power is directly proportional to v³

Efficiency

Useful output energy/total input energy

OR

1 - wasted energy/total input energy

Hooke’s Law: F=

kx

Gradient of force extension graph

k

Total k of springs in series

1/kT is equal to 1/k1 + 1/k2 + 1/k3 …

Total k of springs in parallel

kT = k1 + k2 …

Elastic potential energy

0.5ke²

Area under force extension graph

Elastic potential energy

EPE derivation

Hooke’s Law force-extension area under graph = 0.5 Fx = 0.5 kxx = 0.5 kx²

Tensile stress (unit Pa)

Force / cross-sectional area

Tensile stress (dimensionless)

Extension / original length

Young’s Modulus (Pa or Nm^-2)

Tensile stress/ Tensile strain

ONLY applies to linear part of graph

Connection between Young’s Modulus and k

Young’s modulus E = (F/A) / (x/L) = (F/x) x (L/A)

F = (EA/L)x = kx

Energy Density

Energy/volume = 0.5Fx/AL= 0.5 (F/A) / (x/L) = 0.5 x stress x strain

Force on object if mass is constant

F= (mv-mu)/t = m(v-u)/t = ma

Linear momentum (kgms^-1)

Mass x velocity

Force and momentum relationship equation

Since force is directly proportional to rate of change of momentum (Newton’s 2nd Law), F= k(change in momentum)/t, but k happens to equal 1 so

F= change in momentum/ time taken

Impulse (Ns)

Force x time taken = change in momentum

Area under force-time graph

Change in momentum (impulse)

For momentum diagrams, conservation of momentum applies to each direction independently

Elastic collision

Total KE before = Total KE after

Suggest how F= change in momentum/time can be used to enhance performance of sportspeople

By increasing time taken, smaller force used to produce same change in momentum. For ball to move away at fastest velocity, must keep in contact with ball for as long as possible. Can in tease momentum (and this speed) for given force

e

1.6 × 10^-19 C

Q

± ne, where n is no. of e- added/removed

I (current)

Change in Q/ change in t

1A is how many e-

6.25 × 10^18

Kirchhoff’s 1st Law

Sum of I in = Sum of I out

Mean Drift Velocity

I = Anev (I go to ANE Fast for my jaw)

From mean drift velocity, relationship between A and v

• If we change A, we know from K’s first law I doesnt change, and n and e are constants

• Cancelling terms gives A1V1 = A2V2

Mass of e-

9.11 × 10^-31

Potential difference V

W.D/Q

Cathode ray tube W.D of e-

eV = 0.5mv²

From:

• w.d in accelerating e- is eV (from V=W.D/Q)

• KE of e- =0.5mv²

Velocity of e- in electron gun

v= root (2eV/m)

Resistance

V/I

Resistivity p

R = pL/A

• R is resistance in ohms

• p is resistivity in ohmic metre (ohm m)

• L is length of wire

• A is cross sectional area

How to conclude after proving an equation is homogeneous

LHS = RHS therefore homogeneous

All power equations

• P=W/t

• P=IV

• P=I²R

• P=V²/R

• P=QV/t

Work done related to I and V equation

W=ItV

Cost of electricity

No. of kWh x unit cost

Kirchhoff’s 2nd Law

Sum of p.ds = sum of emfs

Emf and internal resistance equation

Emf = terminal p.d + lost volts

= V + Ir

If circuit resistance is R, what is emf and internal resistance equation

V = IR so from E=V+Ir,

E=I(R+r)

Can arrange it as equation of line:

V= -Ir + E

Power, emf and internal resistance relationship

• P = I²R

• I = E/(R+r)

• P= E²R/ (R+r)²

Potential Dividers Equation

V{out} = V{in} ( R{2} / [R{1} + R{2}] )

Wave speed v

Wavelength x frequency

Wave frequency

1/T

Equation if sinusoidal wave with amplitude A

• y = A sin( kx - wt) for waves moving to right

• y = A sin( kx + wt) for waves moving to left

• k= 2pi/wavelength

• w= 2pi/Time period

Result for superposition of 2 identical waves moving in opposite directions

y = 2A sin(kx) cos(wt)

As time t evolves, cost (wt) oscillated between +1 and -1 so max. displacement from any point x are:

• y max. = +2A sin(kx)

• Y min. = -2A sin(kx)

Phase Difference

• 360x/wavelength - in degrees

• 2pi x/wavelength - in radians

Intensity of waves

Power/surface area

Surface area usually for sphere, so:

Power/4pi r²

Relationship between intensity and amplitude

Since avg. speed of oscillations proportional to amplitude, and KE = 0.5mv³, KE is proportional to amplitude² hence:

Intensity is directly proportional to amplitude²

Because: when waves spread, Intensity drops as energy become more spread out and amplitude decreases