ChemE 123 LE2 Conceptual
5.0(2)
5.0(2)
Card Sorting
1/101
There's no tags or description
Looks like no tags are added yet.
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
102 Terms
1
New cards
Partial molar volume in an ideal-gas mixture
\
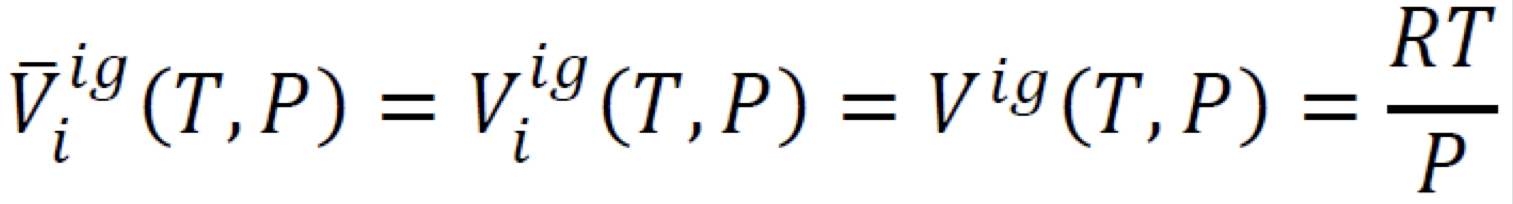
2
New cards
Gibbs’ Theorem (Ideal-gas properties)
A partial molar property (other than volume) of a constituent species in an ideal-gas mixture is equal to the corresponding molar property of the species as a pure ideal gas at the mixture temperature but at a pressure equal to its partial pressure in the mixture.
3
New cards
Gibbs’ Theorem (Ideal-gas properties) Formula
\
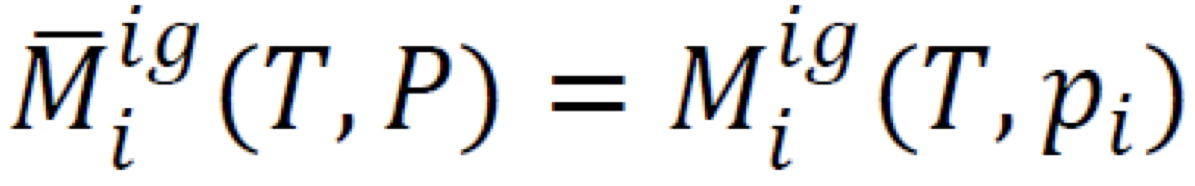
4
New cards
Partial molar enthalpy in ideal-gas mixture
Pressure has no effect on enthalpy
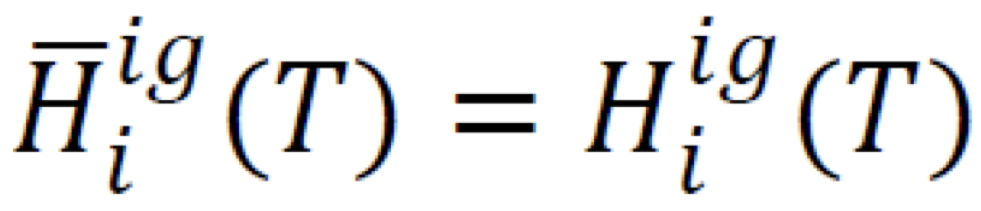
5
New cards
Partial molar entropy in ideal-gas mixture
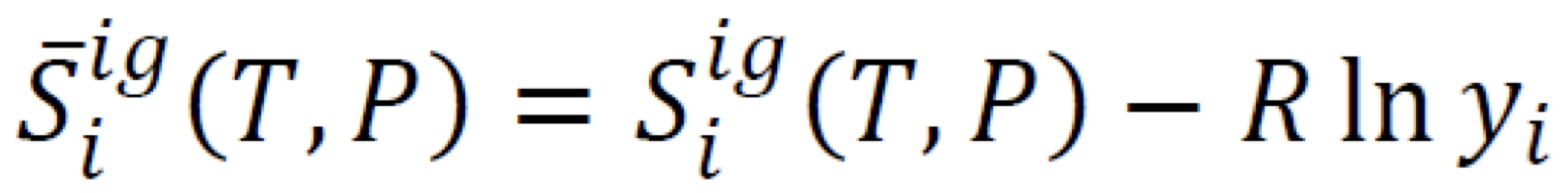
6
New cards
Partial molar Gibbs’ energy in ideal-gas mixture (1)
Simplest possible composition dependence, based on entropy increase due to random intermixing of molecules
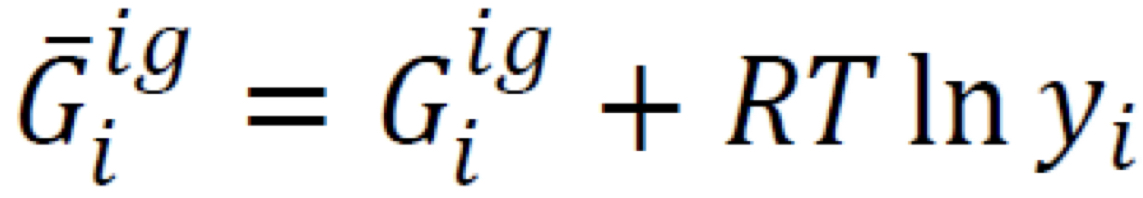
7
New cards
Partial molar Gibbs’ energy in ideal-gas mixture (2)
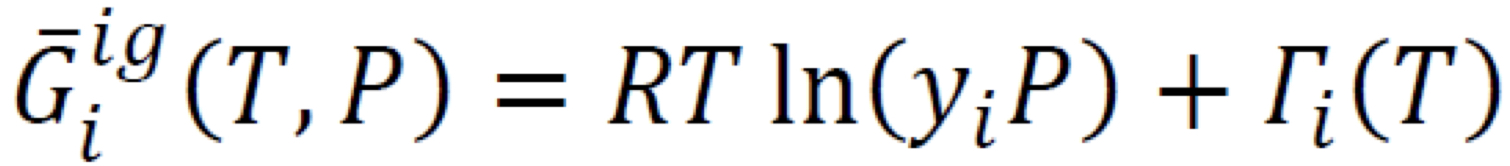
8
New cards
Solution property (summability relation)
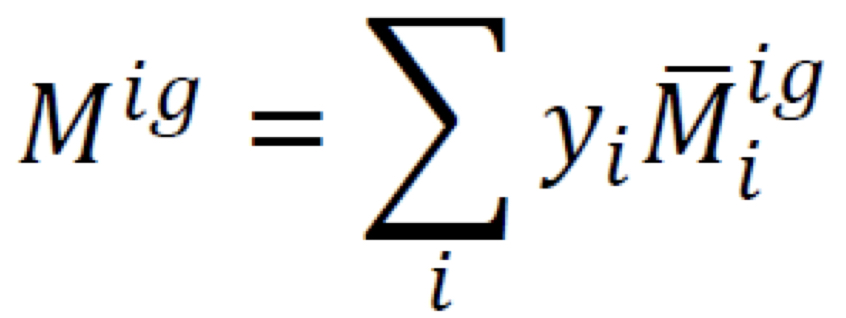
9
New cards
Property change of mixing (at the same conditions, constant T and P)
\
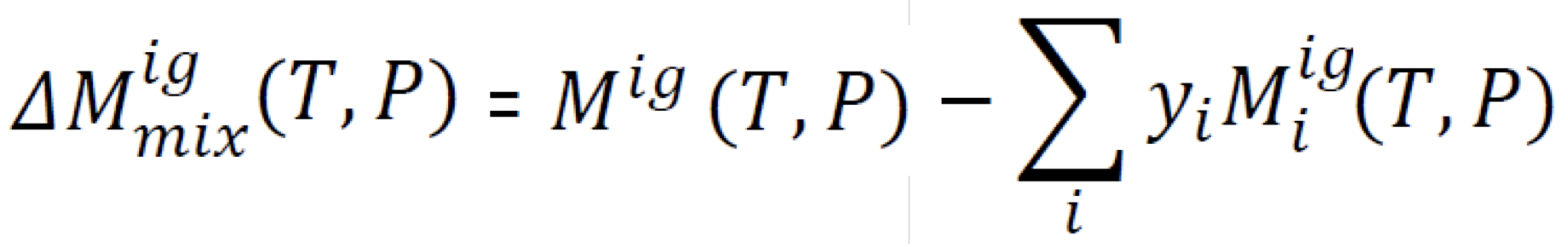
10
New cards
Volume change of mixing
ΔV_mix = V - x1V1 - x2V2
11
New cards
Enthalpy change of mixing
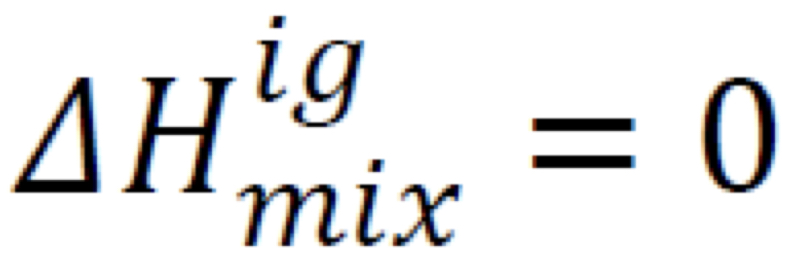
12
New cards
Entropy change of mixing
Always positive (mixing = more molecular disorder)
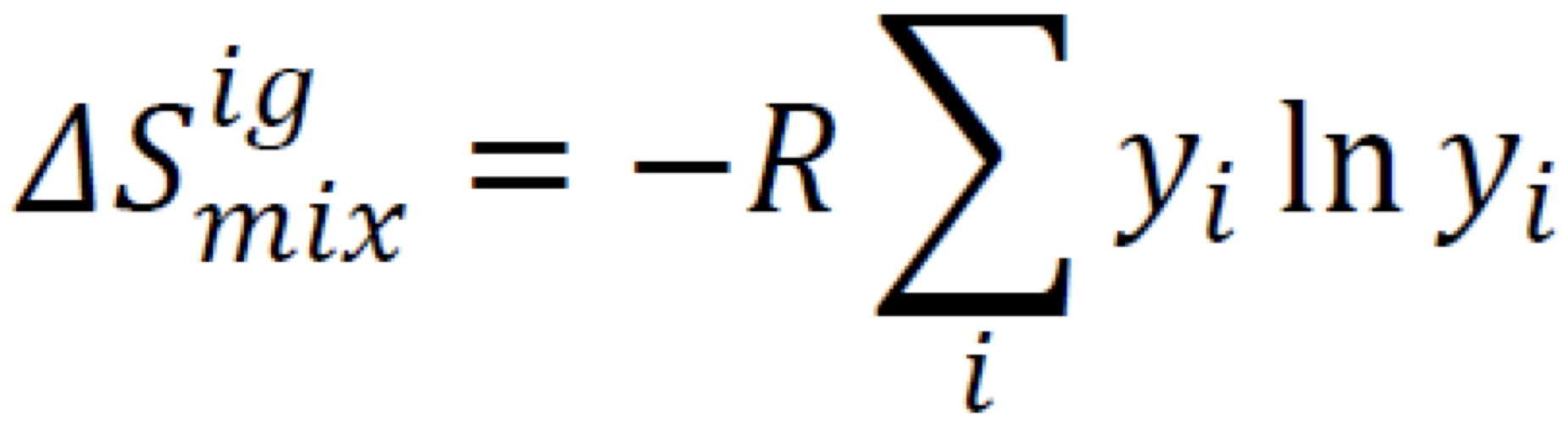
13
New cards
Gibbs Energy Change of Mixing
Always negative (mixing = spontaneous)
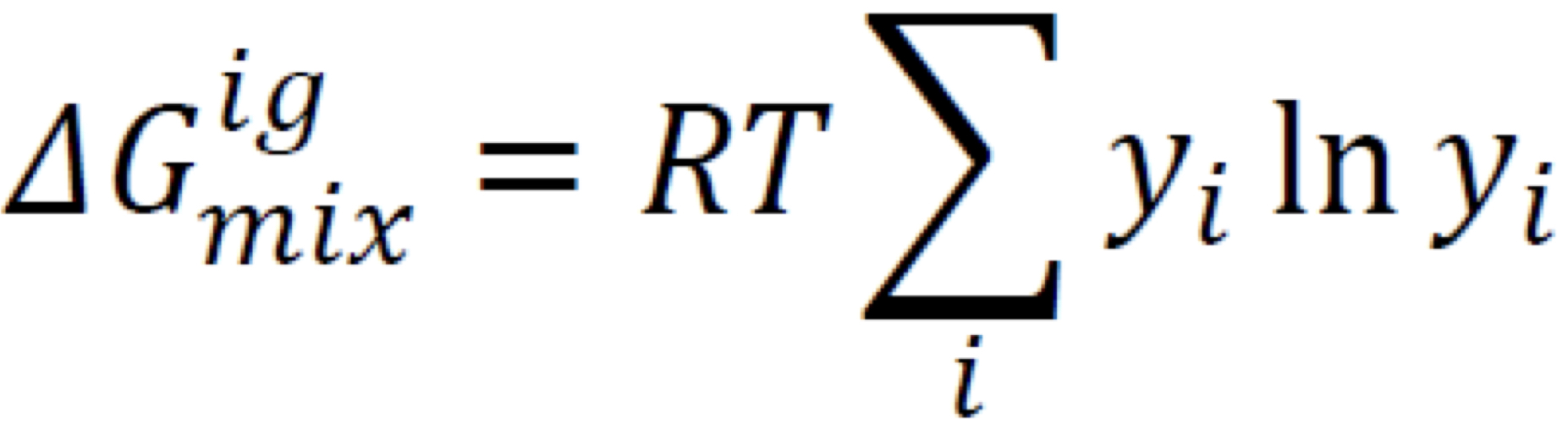
14
New cards
Gibbs Energy Change of Mixing (Summability relation)
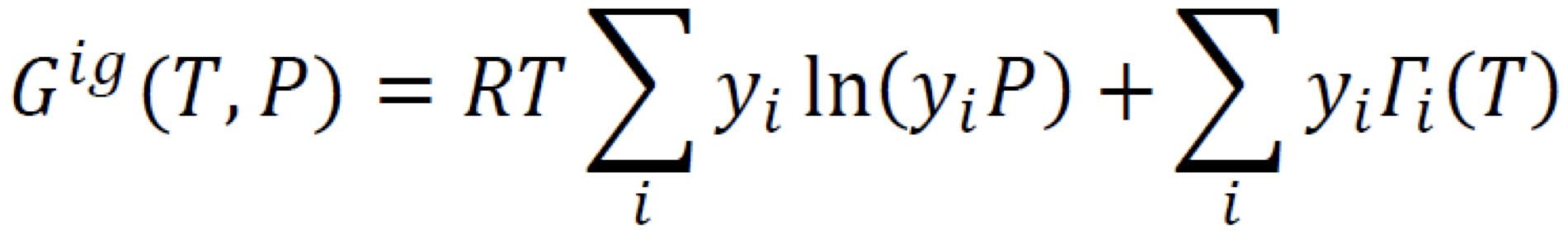
15
New cards
Overall change in property
ΔM = ΔM_i + ΔM_j + … + ΔM,ig_mix
16
New cards
Property change of demixing
ΔM,ig_demix = -ΔM,ig_mix
17
New cards
Phase Equilibrium (Gibbs energy)
For α- and β-phases of a pure species in equilibrium, Gibbs free energies ARE equal (G𝜶 = G𝜷)
18
New cards
Phase equilibrium (chemical potential)
For multiple π phases with N number of species at same T and P in equilibrium, µ𝜶_i = µ𝜷_i = … = µπ_i
19
New cards
Vapor-liquid equilibrium (chemical potential)
µV_i = µL_i
20
New cards
Chemical potential as equilibrium criterion
𝜇𝑖 = 𝐺𝑖_bar; Gibbs energy only defined as (𝑈) and entropy (𝑆). U = no absolute values, 𝜇𝑖 = no absolute values
21
New cards
Chemical potential in ideal gas mixtures
As either P or yi approaches zero, μi_ig becomes negative infinity which is not only applicable to ideal gas but to all kind of gas; not applicable to dilute systems (yi → 0)
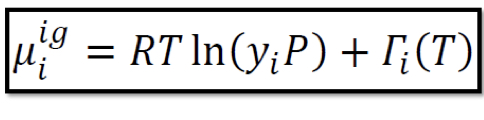
22
New cards
Fugacity as equilibrium criterion
New criterion for equilibrium
23
New cards
Fugacity
For real, pure species (f_i); analogous to pressure, also in pressure units
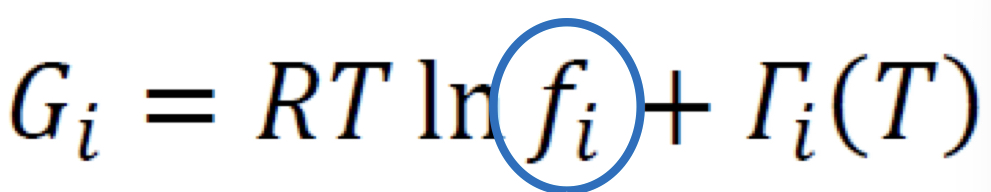
24
New cards
Fugacity of pure, ideal gas
fi_ig = P
25
New cards
Fugacity coefficient of pure species
Φi = fi/P
26
New cards
Fugacity coefficient of pure species and residual Gibbs energy
ln (Φi) = Gi_R/RT
27
New cards
Fugacity coefficient for pure ideal gas
Φi = fi/P = 1
28
New cards
Residual gas volume
Difference between the real gas volume, Vi and the ideal gas volume, Vi_ig.
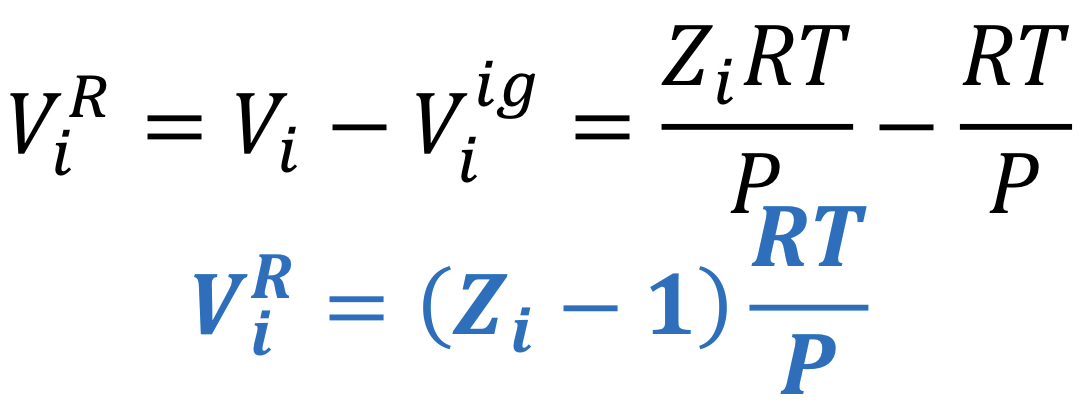
29
New cards
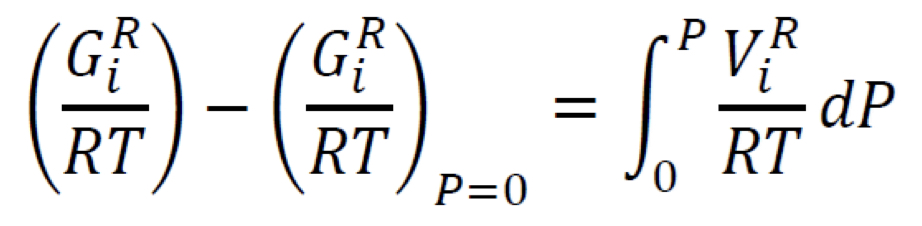
Residual Gibbs energy
In terms of compressibility factor Z

30
New cards
Fugacity coefficient of Pure Gas (VEOS) \[Pitzer\]
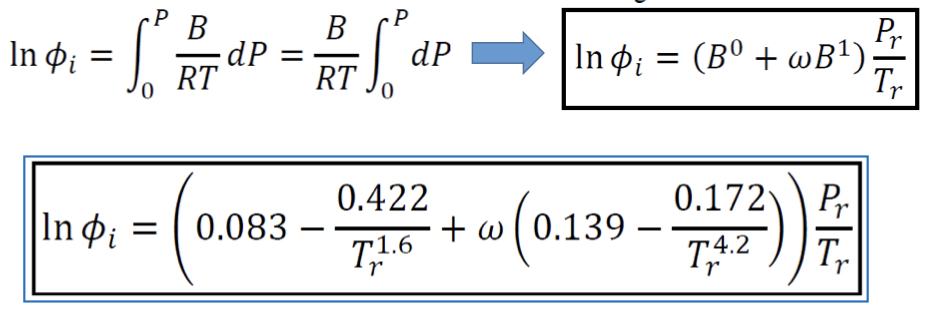
31
New cards
Fugacity coefficient of Pure Gas (VEOS) \[Lee-Kesler\]
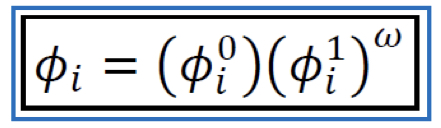
32
New cards
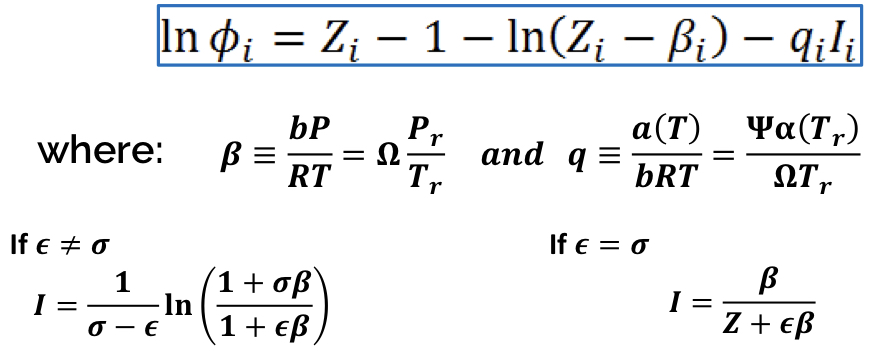
Fugacity coefficient of Pure Gas (CEOS)
Z_int = 1
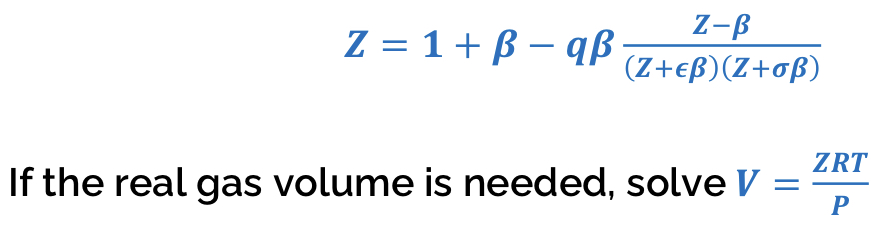
33
New cards
Gibbs energy at equilibrium
Delta_G = 0
34
New cards
Fugacity of Vapor and Liquid Phases at Equilibrium
fi_v = fi_l = fi_sat; for a pure species, the liquid and vapor phases are in equilibrium when they have the same **temperature**, **pressure**, and **fugacity** (criterion).
35
New cards
Fugacity Coefficient of Vapor and Liquid Phases at Equilibrium
Φi_v = Φi_l = Φi_sat
36
New cards
Fugacity of a Pure Subcooled Liquid
For Φi_sat: use EOS and evaluate at Pi_sat
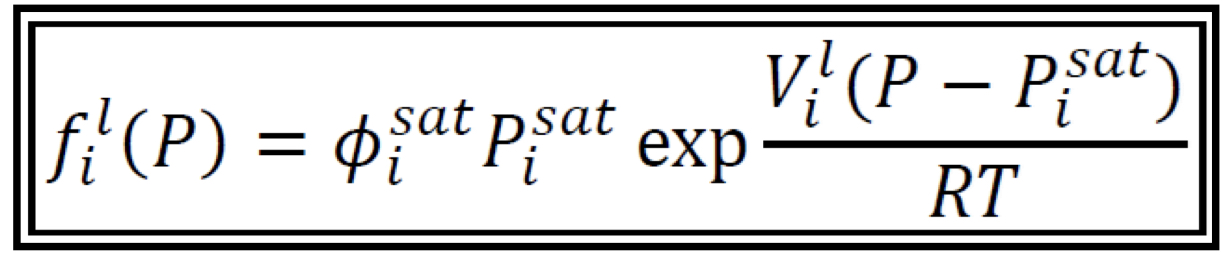
37
New cards
Assumption for fugacity of pure subcooled liquid
Vi_l is considered as a property having weak dependence on pressure at a temperature less than the species’ critical temperature; assumed constant and equal to the saturated liquid-phase molar volume, V_sat
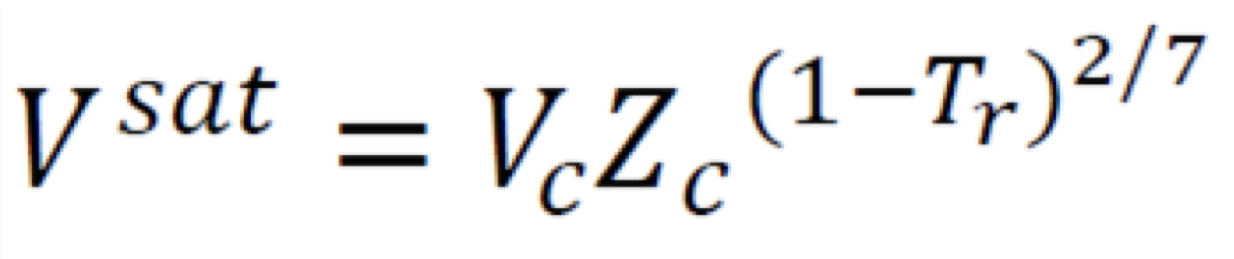
38
New cards
Chemical potential of species in solution
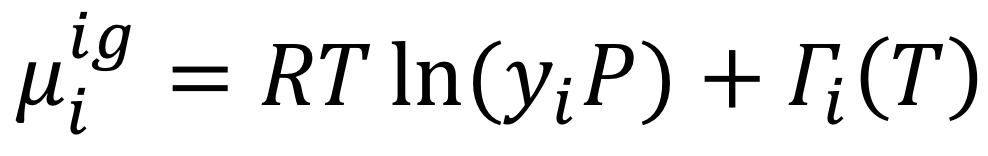
39
New cards
Fugacity of species in solution

40
New cards
Fugacity of ideal gas species in solution
fi_hat_ig = y_i\*P = p_i
41
New cards
Phase equilibrium (fugacity)
Multiple 𝜋 phases with 𝑁 number of species at same T and P are in equilibrium when the fugacity of each constituent species is the same in all phases. fi_hat_𝜶 = fi_hat_ 𝜷 = … = fi_hat_ π
42
New cards
Vapor-liquid equilibrium (fugacity)
fi_hat_v = fi_hat_l
43
New cards
Partial residual property
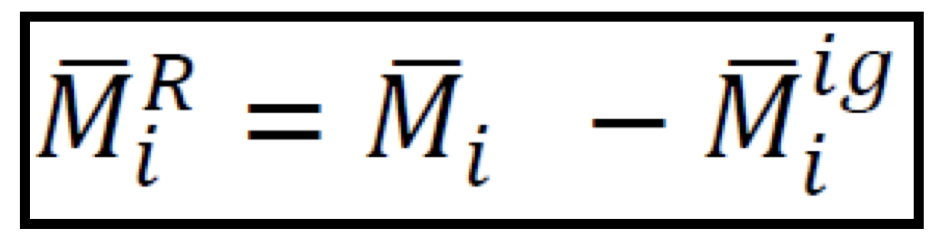
44
New cards
Partial residual Gibbs energy
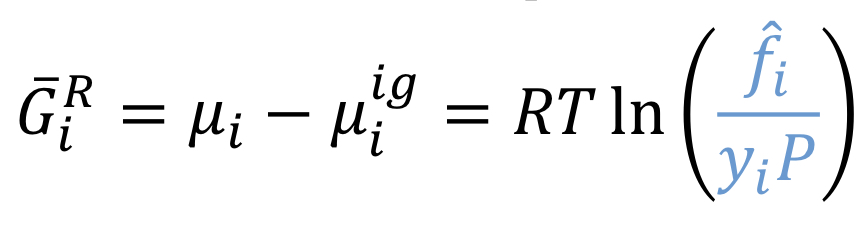
45
New cards
Fugacity coefficient of species in solution
Φi_hat = fi_hat/yi\*P
46
New cards
Fugacity coefficient of pure species in solution and partial residual Gibbs energy
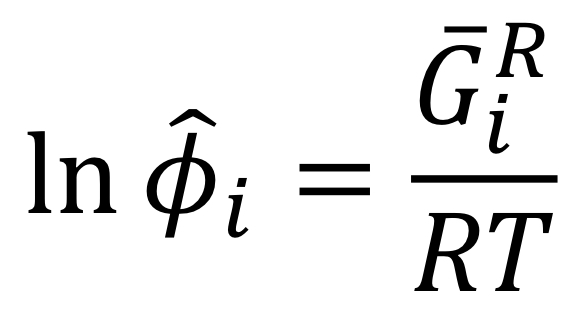
47
New cards
Fundamental residual property relation (derivation)
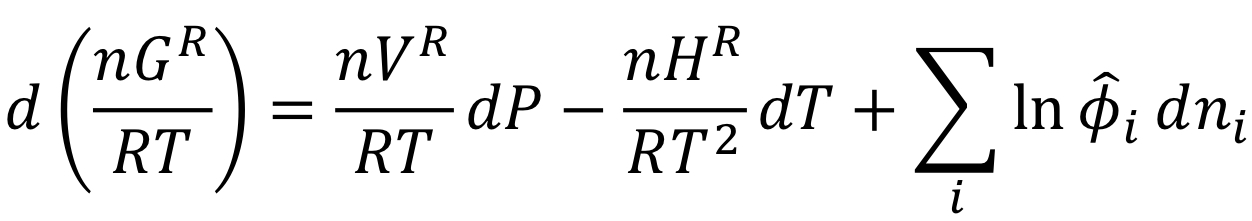
48
New cards
Fundamental residual property relation (Gibbs energy)
At constant temperature, pressure, and, 𝑛_𝑗≠𝑖
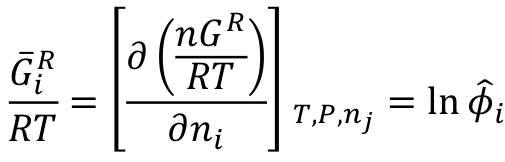
49
New cards
Fugacity coefficient of species in solution (Z-terms)
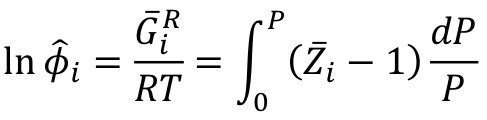
50
New cards
Second virial coefficient (B)
For pure gas, only a function of **temperature**; for gas mixtures, function of **both temperature and composition**
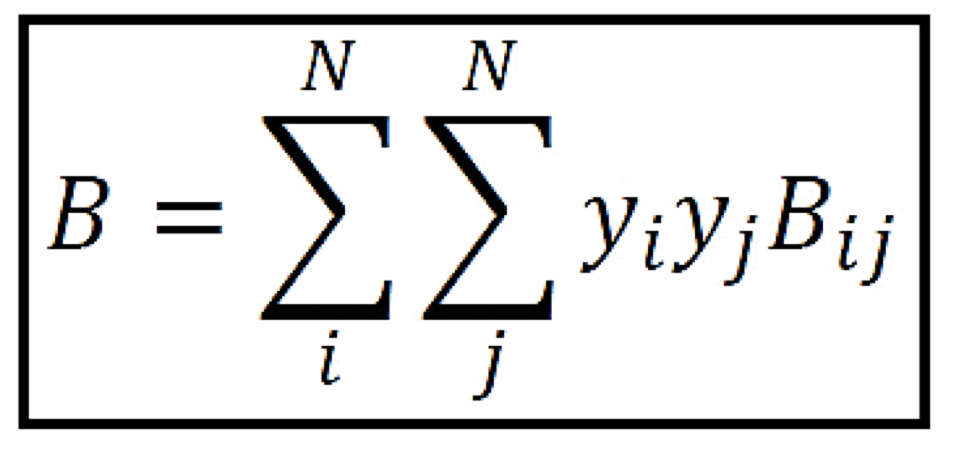
51
New cards
Cross coefficient (B_ij)
Characterizes the bimolecular interaction between species i and j
52
New cards
Fugacity coefficient of species in solution (VEOS)

53
New cards
Vapor side expression of VLE criterion
For the vapor and liquid phase with N number of species at same T and P in equilibrium:
fi_hat_v = fi_hat_l
fi_hat_v = yi\*Φi_hat\*P
fi_hat_v = f(T, P, yi)
fi_hat_v = fi_hat_l
fi_hat_v = yi\*Φi_hat\*P
fi_hat_v = f(T, P, yi)
54
New cards
Ideal solution
Ideal mixture of gases, liquids, or solids
55
New cards
Ideal solution model partial molar Gibbs energy
mole fraction is denoted as 𝑥𝑖 since this model is often used for mixture of liquids; ideal gas mixture: xi → yi
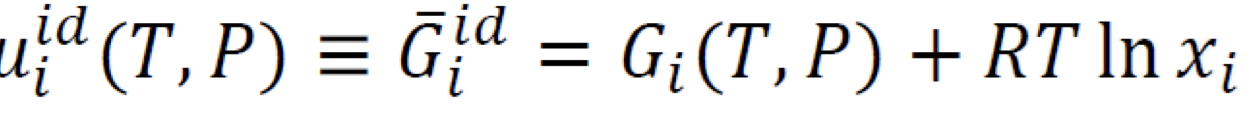
56
New cards
Ideal solution volume
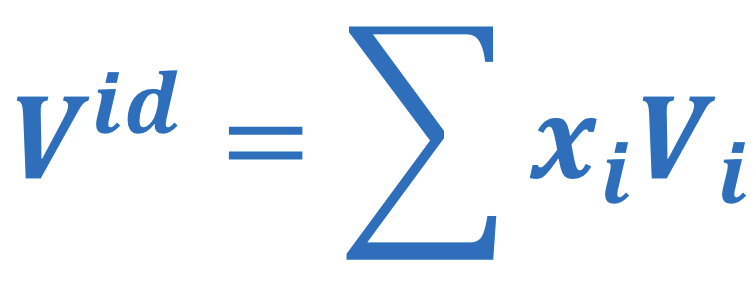
57
New cards
Ideal solution entropy
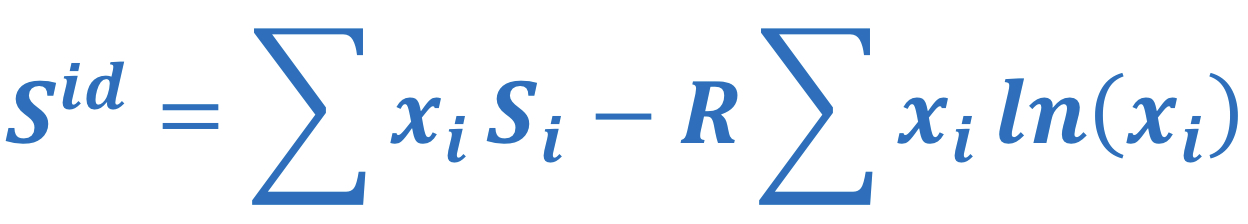
58
New cards
Ideal solution enthalpy
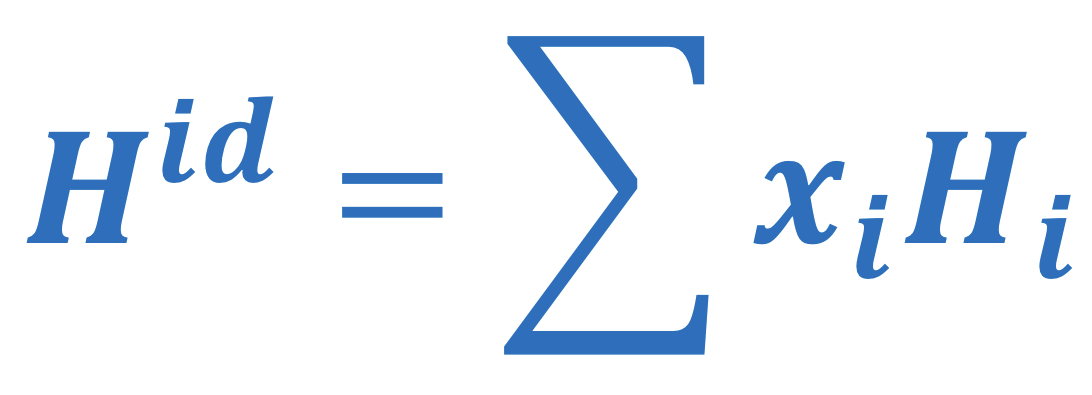
59
New cards
Lewis/Randall Rule (fugacity)
Applies to each species (solid, liquid, or gas) present in an ideal solution; fugacity of each species in an ideal solution (fid_hat) is directly proportional to its composition (xi), with proportionality constant equal to pure species fugacity (fi)
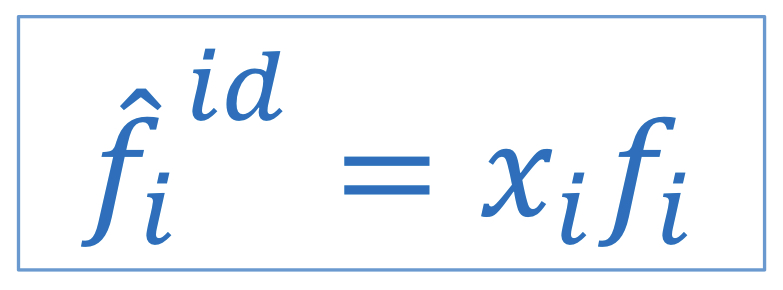
60
New cards
Lewis/Randall Rule (fugacity coefficient)
Fugacity coefficient of a species in an ideal solution, 𝜙i_hat_id, is equal to the pure species fugacity coefficient, 𝜙i.
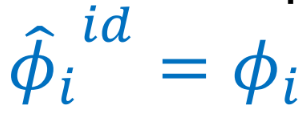
61
New cards
Activity coefficient of species in ideal solution
γi = fi_hat/xi\*fi
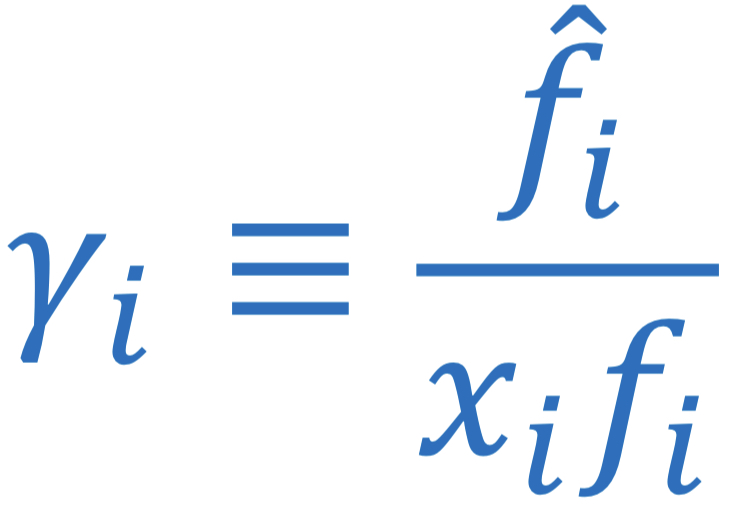
62
New cards
Excess property
Difference between real solution property and ideal solution property
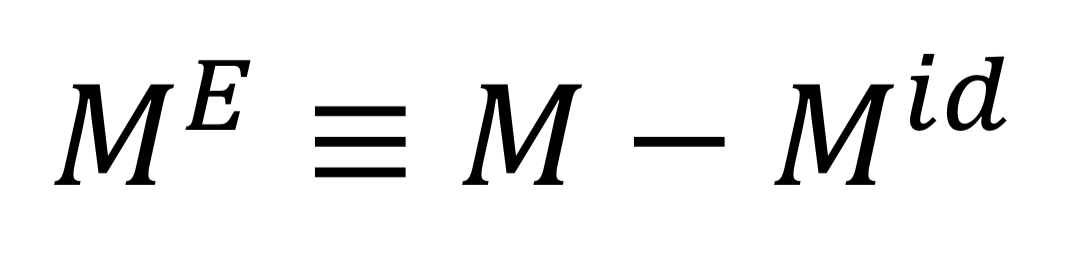
63
New cards
Activity coefficient and excess Gibbs energy
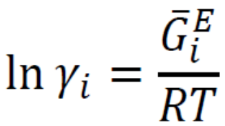
64
New cards
Chemical potential in different solution models

65
New cards
Molecular interactions in different solution models
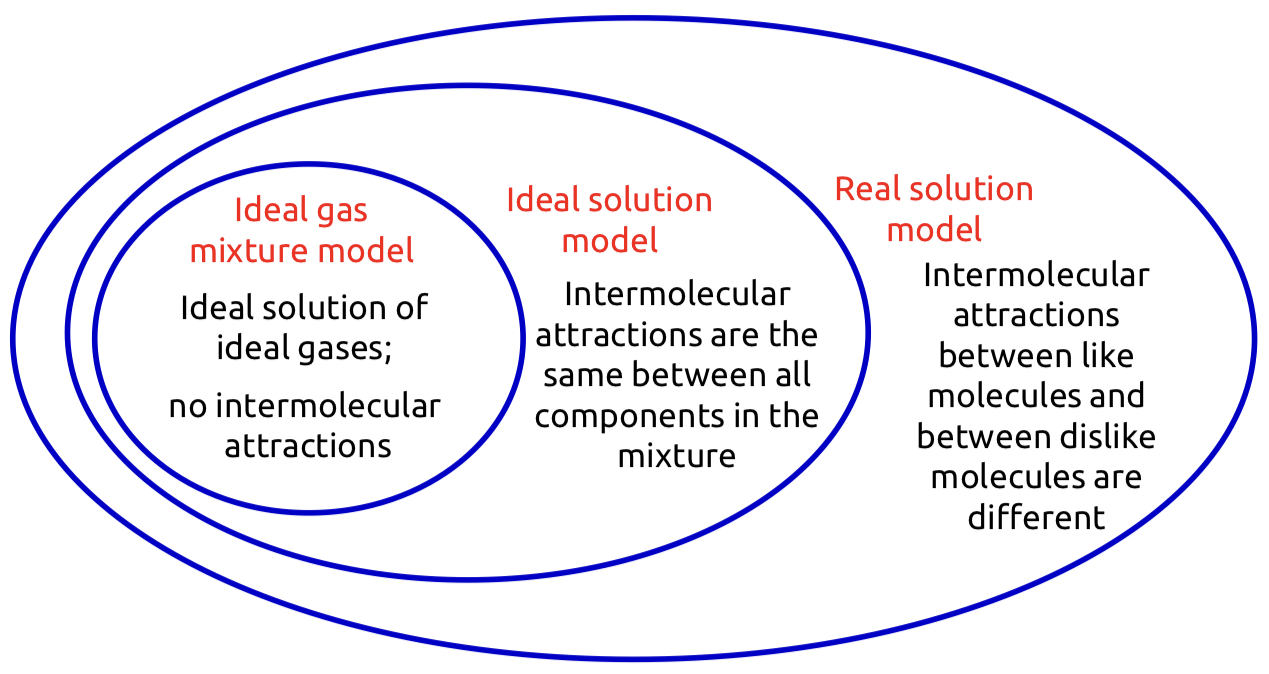
66
New cards
Fugacity and fugacity coefficients in different solution models
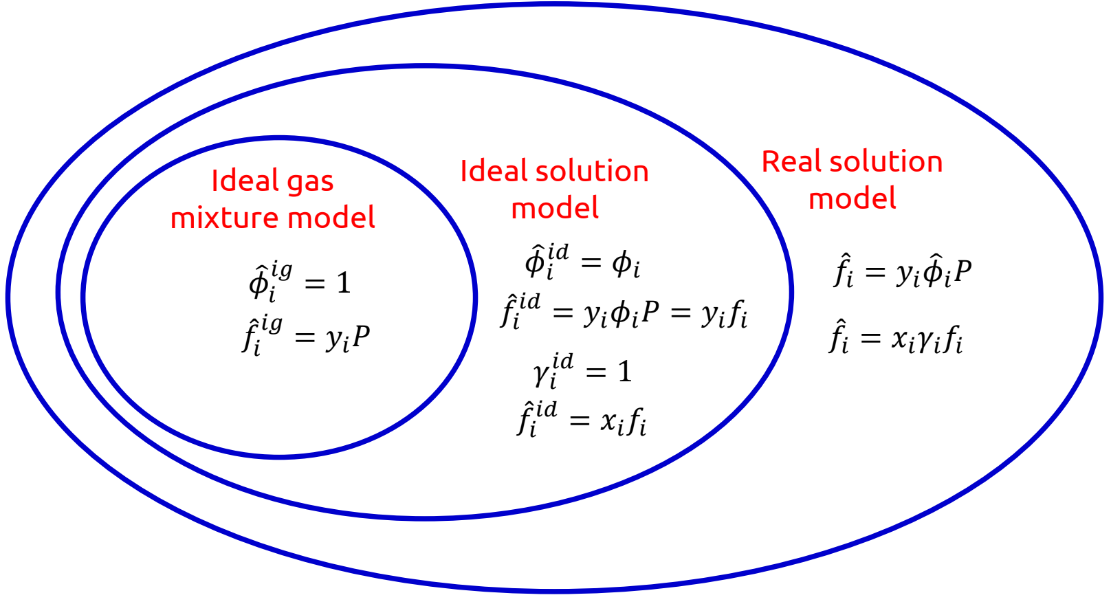
67
New cards
Gamma/Phi formulation of VLE
Assuming that Vi_l is weakly dependent on pressure at a temperature lower than the species’ critical temperature
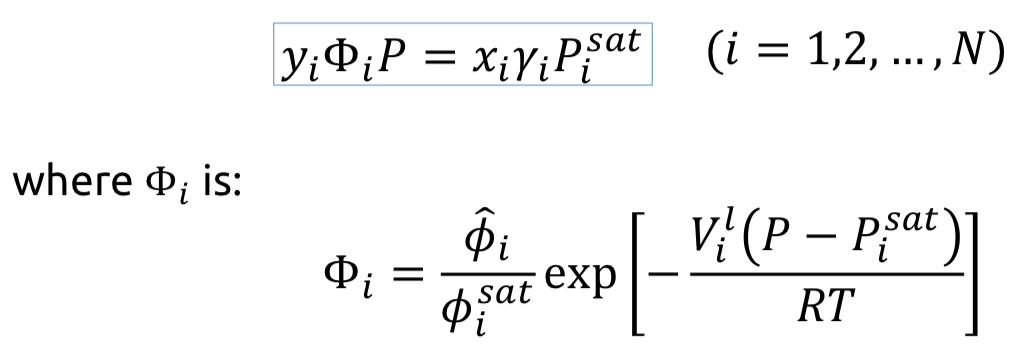
68
New cards
Excess Properties and Residual Properties
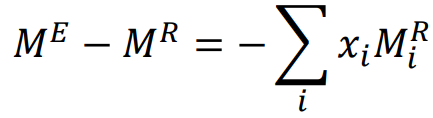
69
New cards
Fundamental excess property relation
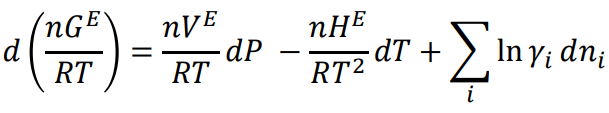
70
New cards
Equations for excess properties
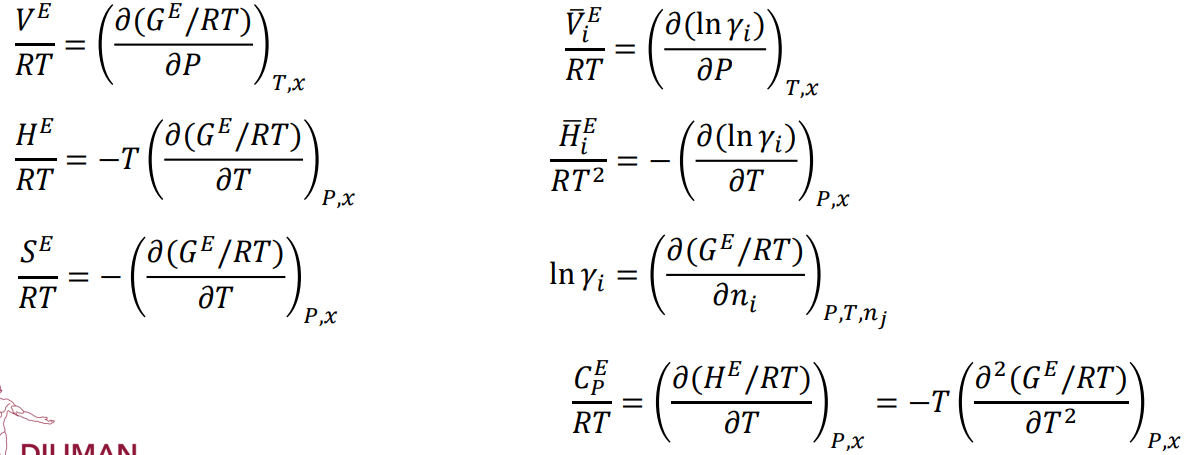
71
New cards
Nature of Excess Properties
* No meaning for pure species
* Excess properties are often strong functions of temperature.
* At normal temperatures, they are not strongly influenced by pressure.
* Excess properties are often strong functions of temperature.
* At normal temperatures, they are not strongly influenced by pressure.
72
New cards
Plot of G_E , H_E , and S_E vs. composition
1. All excess properties become **zero** as either species approaches **purity**.
2. Although G_E vs. x1 is approximately parabolic in shape, both H_E and TS_E exhibit individualistic composition dependencies.
3. When an excess property M_E has a **single sign**, the **extreme value** of M_E (**maximum or minimum**) often occurs **near the equimolar composition**.
73
New cards
VLE Data
* At xi = yi = 0, fi_hat = 0
* At xi = yi = 1, fi_hat = fi_ig = Pi_sat
* For ideal gas, at xi = 1, ɣi = 1, at xi = 0, ɣi = indeterminate
* At xi = yi = 1, fi_hat = fi_ig = Pi_sat
* For ideal gas, at xi = 1, ɣi = 1, at xi = 0, ɣi = indeterminate
74
New cards
Rational functions
* No theoretical foundation
* Cannot be extended to mixtures with more than two components
* No temperature dependence
* Cannot be extended to mixtures with more than two components
* No temperature dependence
75
New cards
Local composition
* Composition in a local volume around a molecule
* May be different from overall mixture composition
* Presumed to account for the short-range order and nonrandom molecular orientations arising from the molecule’s size and IMFs.
* May be different from overall mixture composition
* Presumed to account for the short-range order and nonrandom molecular orientations arising from the molecule’s size and IMFs.
76
New cards
Local composition models
* Founded on statistical mechanics instead of being arbitrary
* Can be extended to multi-component systems while requiring only binary interaction parameters
* Incorporates temperature dependence
* Can be extended to multi-component systems while requiring only binary interaction parameters
* Incorporates temperature dependence
77
New cards
Wilson Equation
* Works well for mixtures of polar and nonpolar species, e.g. alcohols and alkanes.
* Works well for hydrocarbon mixtures and is readily extended to multicomponent mixtures.
* Wilson parameters, Λij and Λji however, must be positive to be valid for infinite dilution cases.
* Use when components in the liquid phase are completely miscible over the entire composition range
* Unable to describe systems exhibiting partial miscibility
* Works well for hydrocarbon mixtures and is readily extended to multicomponent mixtures.
* Wilson parameters, Λij and Λji however, must be positive to be valid for infinite dilution cases.
* Use when components in the liquid phase are completely miscible over the entire composition range
* Unable to describe systems exhibiting partial miscibility
78
New cards
NRTL Equation
* Widely used for liquid-liquid extraction
* The parameter α characterizes the tendency of species j and i to be distributed nonrandomly.
* Not very appealing from a theoretical perspective, but its flexibility has led to a broad range of applications including combinations with electrolyte models.
* Can be used for highly nonideal systems as well as for partially miscible systems
* Preferred when limited solubility is a feature of the system
* The parameter α characterizes the tendency of species j and i to be distributed nonrandomly.
* Not very appealing from a theoretical perspective, but its flexibility has led to a broad range of applications including combinations with electrolyte models.
* Can be used for highly nonideal systems as well as for partially miscible systems
* Preferred when limited solubility is a feature of the system
79
New cards
UNIQUAC Model
* Uses local area fraction θij as the primary concentration variable
* Comprised of
* **combinatorial effects** due to differences in size and shape
* **residual effects** due to differences in intermolecular forces
* Often gives good representation of VLE and LLE for binary and multicomponent mixtures containing nonelectrolytes
* For hydrocarbons, ketones, esters, water, amines, alcohols, nitriles, etc.
* Comprised of
* **combinatorial effects** due to differences in size and shape
* **residual effects** due to differences in intermolecular forces
* Often gives good representation of VLE and LLE for binary and multicomponent mixtures containing nonelectrolytes
* For hydrocarbons, ketones, esters, water, amines, alcohols, nitriles, etc.
80
New cards
Local area fraction
* Determined by representing a molecule by a set of bonded segments.
* Each molecule is characterized by two structural parameters determined relative to a standard segment.
* Each molecule is characterized by two structural parameters determined relative to a standard segment.
81
New cards
Local area fraction structural parameters
1. r : volume parameter → Relative number of segments per molecule
2. q : surface parameter → Relative surface area
82
New cards
UNIFAC Model
* Theoretically-based way to estimate activity coefficients
* Predictions can be made over a temperature range of 275-425 K and for pressures to a few atmospheres
* All components must be condensable at near-ambient conditions
* A molecule is viewed as an aggregate of functional groups, each comprised of subgroups.
* The relative volume (Rk) and relative surface area (Qk) are properties of the subgroups.
* A fluid mixture property is viewed as the sum of contributions from the molecules’ subgroups instead of the entire molecules.
* Predictions can be made over a temperature range of 275-425 K and for pressures to a few atmospheres
* All components must be condensable at near-ambient conditions
* A molecule is viewed as an aggregate of functional groups, each comprised of subgroups.
* The relative volume (Rk) and relative surface area (Qk) are properties of the subgroups.
* A fluid mixture property is viewed as the sum of contributions from the molecules’ subgroups instead of the entire molecules.
83
New cards
Simple mixtures, with components similar in chemical nature and molecular size
One-parameter Margules
84
New cards
Moderately non-ideal binary mixtures
Margules, van Laar, Wilson, NRTL, UNIQUAC
85
New cards
Strongly non-ideal mixtures (e.g., alcohols + hydrocarbons)
Wilson
86
New cards
Solutions with miscibility gap (LLE)
NRTL, UNIQUAC
87
New cards
Thermodynamic consistency
High consistency if avg. |δln(ɣ1/ɣ2)| < 0.03
Accept if avg. |δln(ɣ1/ɣ2)| < 0.10
Accept if avg. |δln(ɣ1/ɣ2)| < 0.10
88
New cards
Barker’s method
* An alternative method requiring regression that provides better thermodynamic consistency.
* Find values of the parameters that minimize the error: P\* - P
* Find values of the parameters that minimize the error: P\* - P
89
New cards
Data interpretation
Even if data satisfy the tests, the reliability of experimental data is still in question.
90
New cards
Stability criterion (G)
* The equilibrium state of a closed system is that state for which the total Gibbs energy is a minimum with respect to all possible changes at the given T and P.
* all irreversible processes occurring at constant T and P proceed in such a direction as to cause a decrease in the Gibbs energy of the system (negative, spontaneous).
* mixed state must be the one of lower Gibbs energy with respect to the unmixed state.
* all irreversible processes occurring at constant T and P proceed in such a direction as to cause a decrease in the Gibbs energy of the system (negative, spontaneous).
* mixed state must be the one of lower Gibbs energy with respect to the unmixed state.
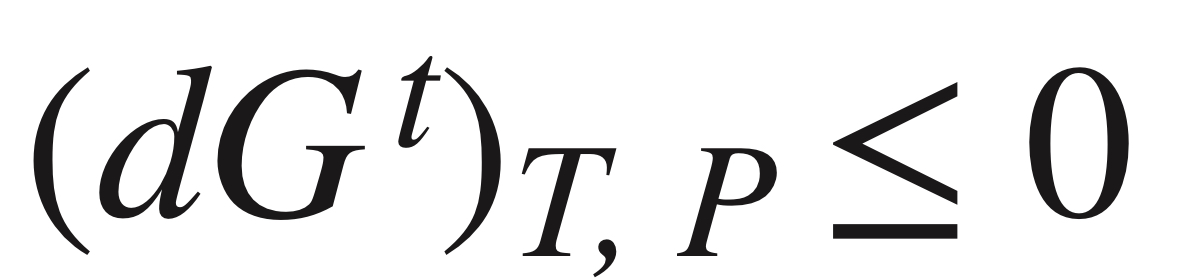
91
New cards
Complete miscibility
Graph of ΔG vs x1 is all concave up (positive second derivative)
92
New cards
Immiscibility
* ΔG vs x1 has concave down (negative second derivative)
* when mixing occurs, a system can achieve a lower value of the Gibbs energy by forming two phases than by forming a single phase
* when mixing occurs, a system can achieve a lower value of the Gibbs energy by forming two phases than by forming a single phase
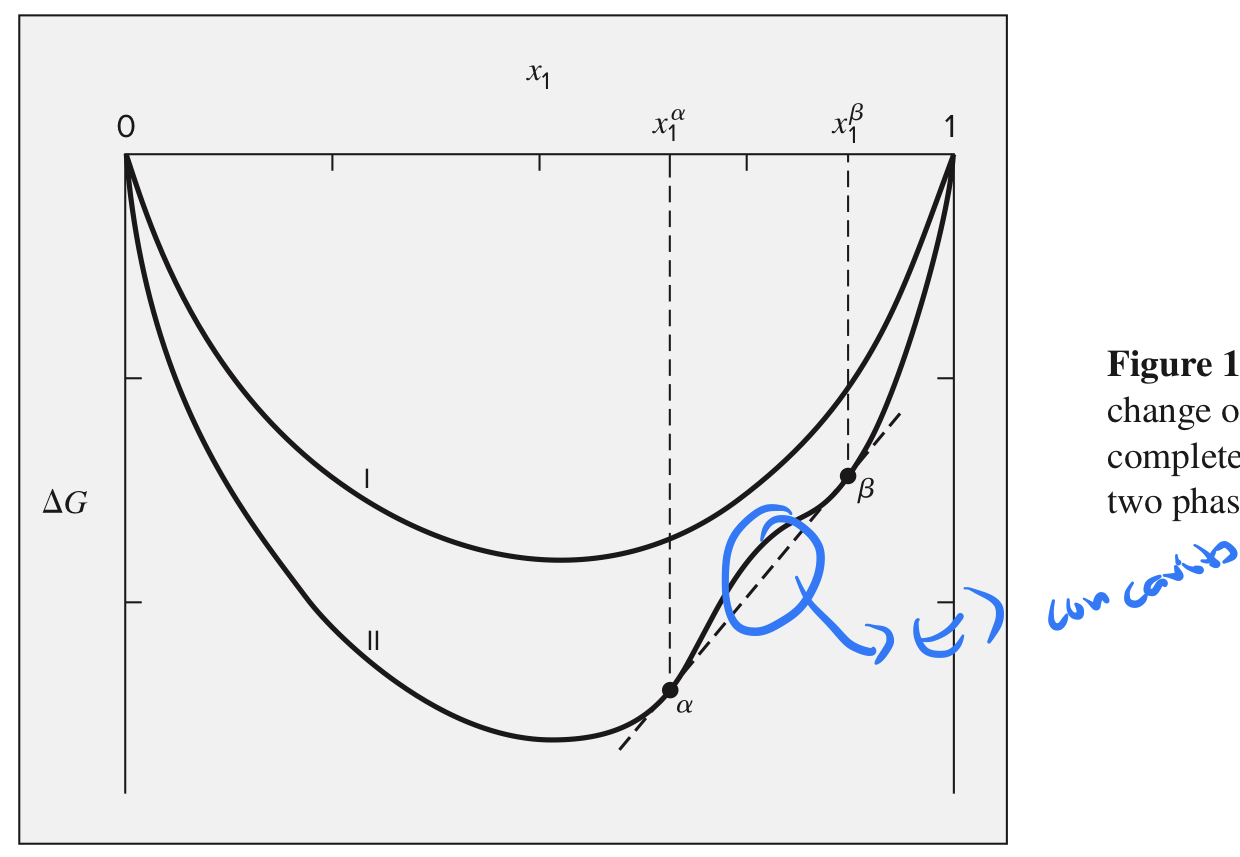
93
New cards
Stability criterion for single-phase binary mixture
At fixed temperature and pressure, a single-phase binary mixture is stable if and only if ΔG and its first and second derivatives are continuous functions of x1, and the second derivative is positive.
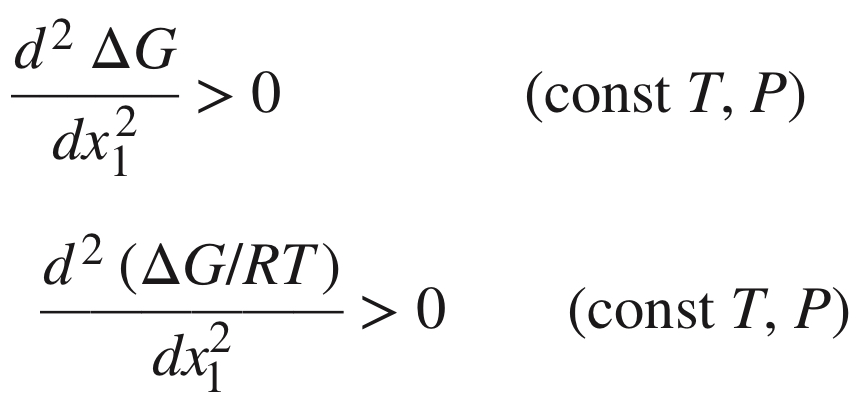
94
New cards
Stability criterion (G_E/RT)
* use activity coefficient models to test
* If true, composition has single phase
* If true, composition has single phase
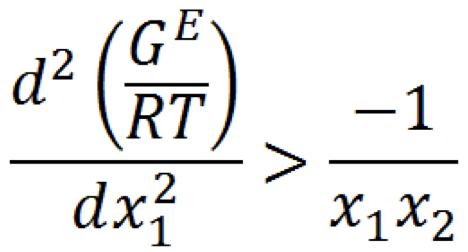
95
New cards
Stability criterion (activity coefficient)
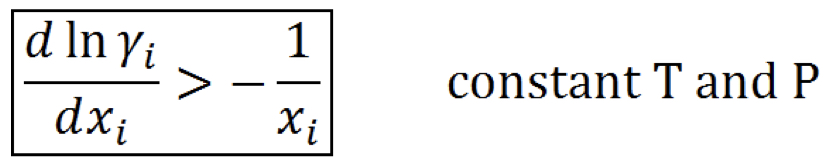
96
New cards
Stability criterion (fugacity)
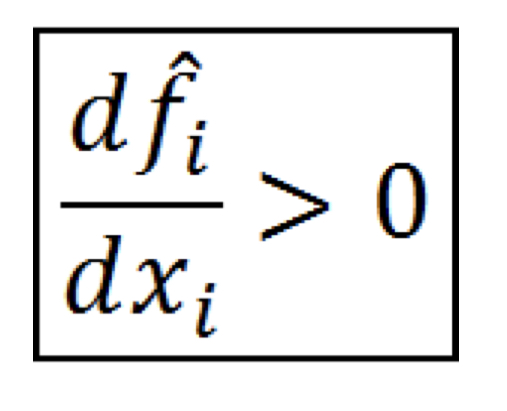
97
New cards
Stability criterion (chemical potential)
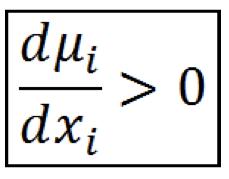
98
New cards
Liquid-liquid equilibrium
When stability criterion breaks, liquid-liquid equilibrium exists. (unstable, 2 liquid phases)
99
New cards
Solubility diagram
* T vs x1
* Curve UAL - α phase (rich in species 2)
* Curve UBL - β phase (rich in species 1)
* Curve UAL - α phase (rich in species 2)
* Curve UBL - β phase (rich in species 1)
100
New cards
x1_α and x1_β phase
* At each temperature, these compositions are those for which the curvature of the ΔG vs. x1 curve changes sign.
* Between these compositions, it is concave down (negative second derivative) and outside them it is concave up.
* At these points, the curvature is zero (inflection points on ΔG vs. x1 curve).
* Between these compositions, it is concave down (negative second derivative) and outside them it is concave up.
* At these points, the curvature is zero (inflection points on ΔG vs. x1 curve).