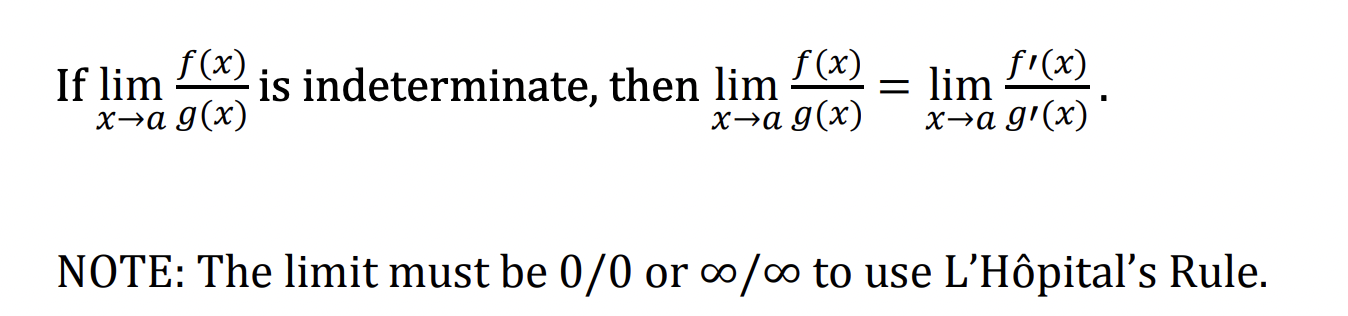TTKs Unit 2- AP Calculus

Things to Know for AP Calculus Unit 2 (majorly formulas)

What is the general definition of a derivative?

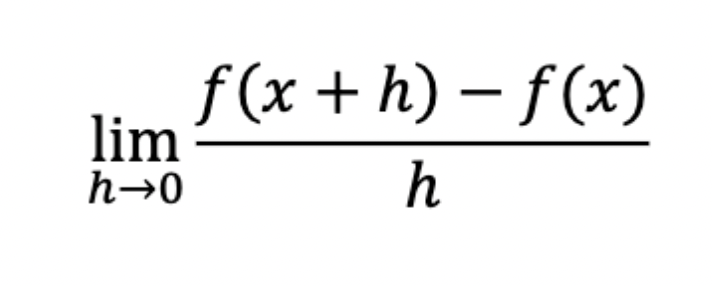
What is the definition of a derivative at any point

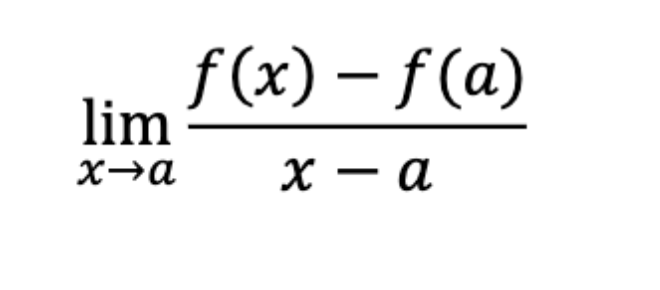
What is the definition of a derivative at x = a

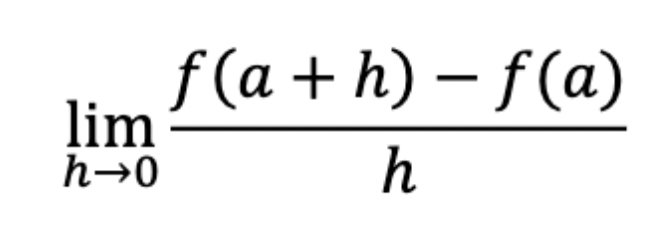
What is the derivative of a function?

The slope of the tangent line

How do you find the equation of the tangent line at x = a

1. Find the derivative of f(x)

2. Plug a in f’(x) to get slope (m)

3. Plug a into f(x) to get y

4. Write the equation in point slope form

How do you find the equation of the normal line at x = a

1. Find the slope of the tangent line

2. Take the negative reciprocal of that slope

3. Write the equation in point slope form using the new slope

What does it mean when a function is differentiable at x = c

The derivative from the left of x = c is equal to the derivative from the right of x = c

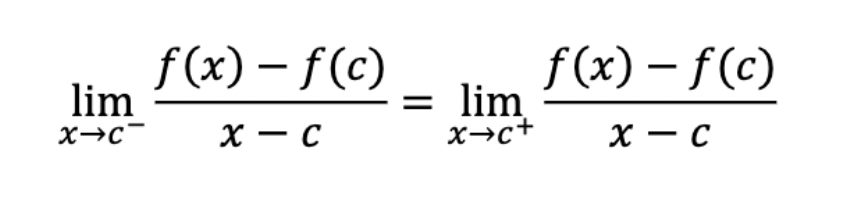
If there is a discontinuity in the original function, is the function differentiable, continuous or neither

Neither. The function is NOT continuous and therefore is NOT differentiable

If there is a discontinuity in the derivative of a function, is the function differentiable, continuous or neither

The derivative is NOT differentiable but may or may not be continuous depending on if that discontinuity is present in the original function

If a function is continuous at a point

It may or may not be differentiable at that point

If a function is differentiable at a point

It is continuous at a that point

What is a horizontal tangent?

The numerator of the derivative = 0

What is a vertical tangent?

The denominator of the derivative = 0

What is a critical point?

If f is defined at c

• f’(c) = 0 or f’(c) = undefined then that is a critical point

What is the first derivative test?

• If f’ changes signs from positive to negative f has a maximum value at c

• If f’ changes signs from negative to positive f has a minimum value at c

• If f’ doesn’t change signs at x = c then f has no relative extrema

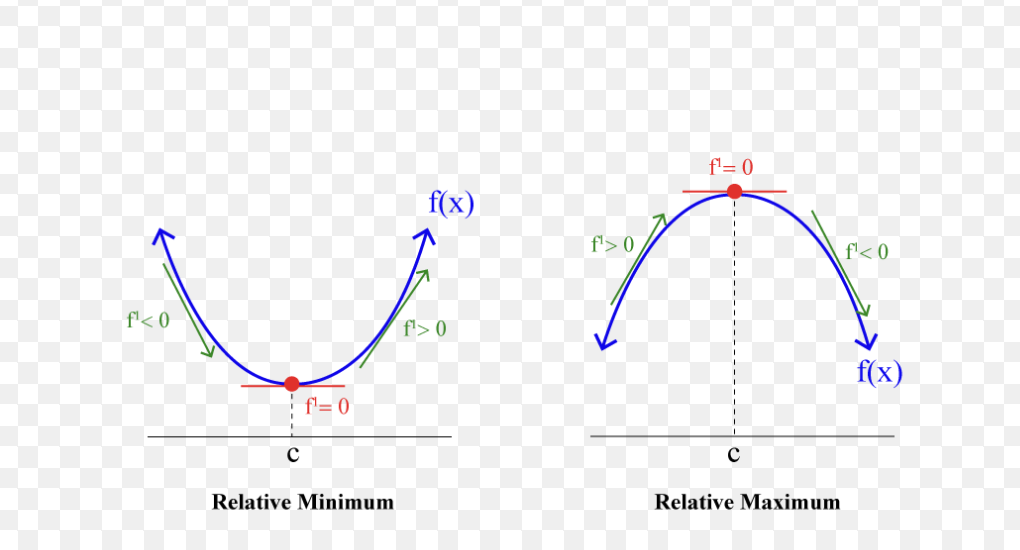
On a closed interval [a,b], if f’<0 and x>a then f

has a relative maximum at x = a. The function is decreasing from the left endpoint so the left endpoint is a relative maximum

On a closed interval [a,b], if f’>0 and x>a then f

has a relative minimum at x = a. The function is increasing from the left endpoint.

On a closed interval [a,b], if f’<0 and x<b then f

has a relative maximum at x = b. The function is increasing into the right endpoint.

On a closed interval [a,b], if f’>0 and x<b then f

has a relative minimum at x = b. The function decreases into the right endpoint

If f is increasing, f’

is positive (f’>0)

If f is decreasing, f’

is negative (f’<0)

How do you find the intervals of increase and decrease

• Find the critical points

• Organize a sign chart

If f”>0 describe what happens to f’ and f

f’ is increasing and f is concave up (like a cup)

If f”<0 describe what happens to f’ and f

f’ is decreasing and f is concave down (like a frown)

When does f have a point of inflection?

When f” changes signs at x

If f’(c) = 0 and f”(c) > 0 then f has

a relative minimum is and is concave up

If f’(c) = 0 and f”(c) < 0 then f has

a relative maximum is and is concave down

What is the formula for chain rule? (2 formulas)

What is the formula for the product rule and quotient rule?

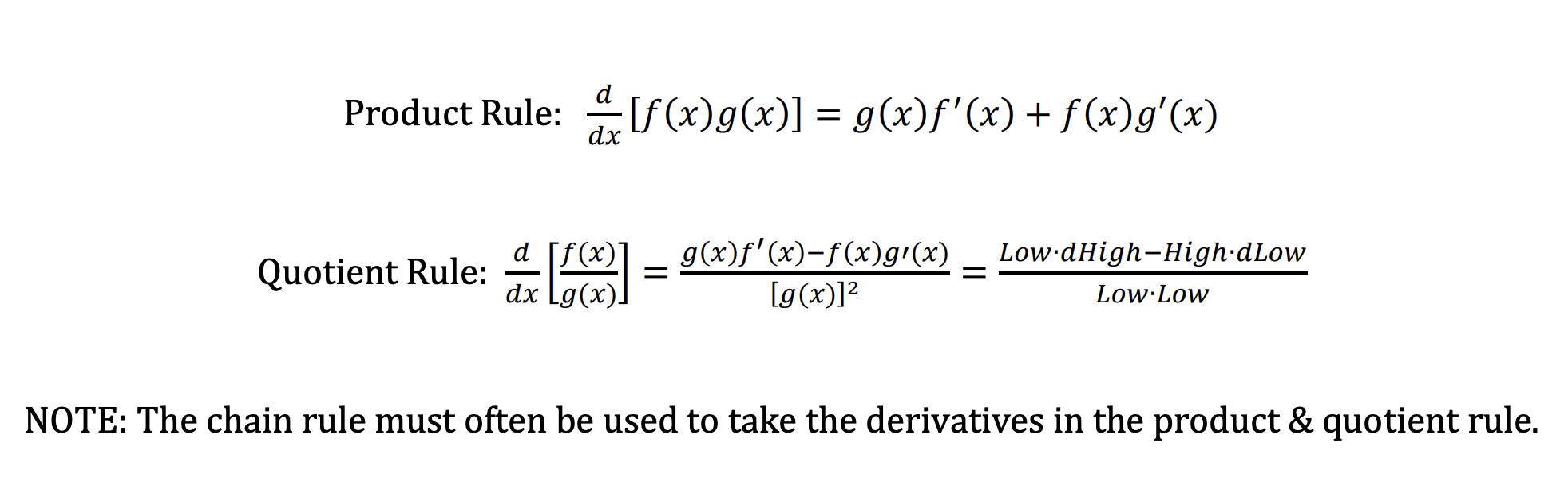
What is the power rule?

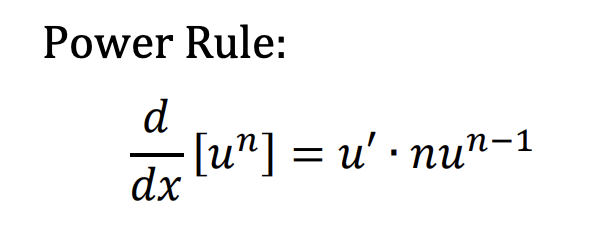
What is the constant rule?

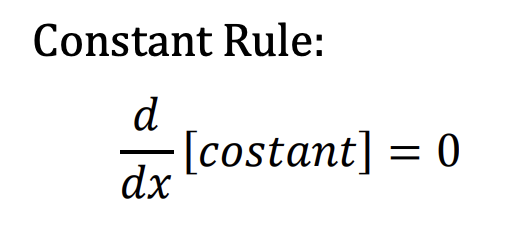
What is the scalar rule

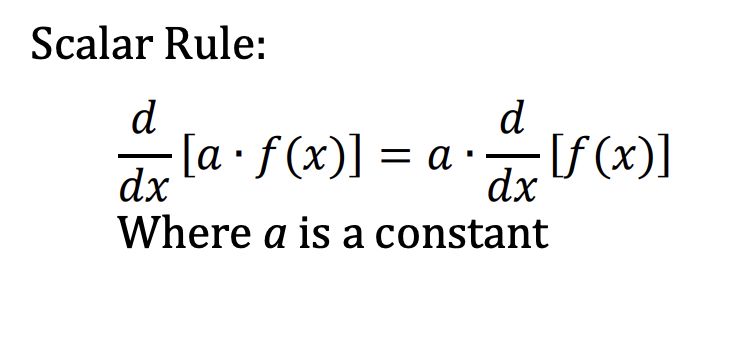
What are the trig derivatives (sin, cos, tan, csc, sec, cot)

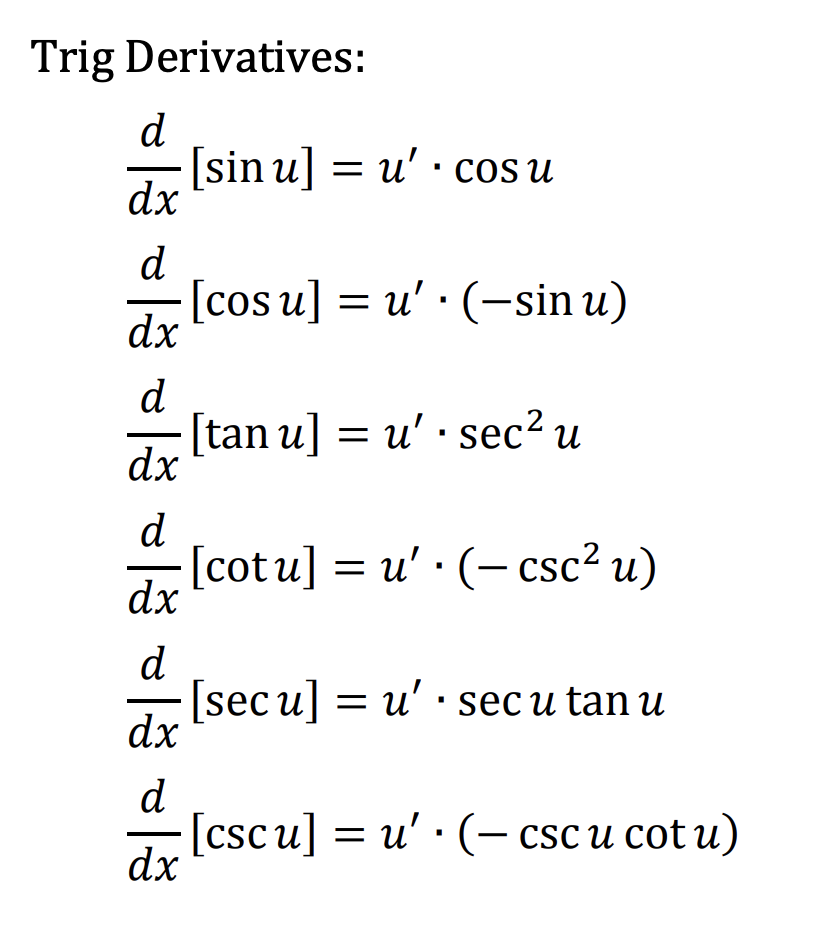
What is velocity?

The derivative of the position : v(t) = s’(t)

When velocity > 0, which direction does it move

It moves in the positive direction either right (x axis) or up (y axis)

When velocity < 0, which direction does it move

It moves in the negative direction either left (x axis) or down (y axis)

When velocity = 0

The object is at rest

What is accleration?

The derivative of velocity and the 2nd derivative of the position

a(t) = v’(t) = s”(t)

When the acceleration > 0, the velocity

is increasing

When the acceleration < 0, the velocity

is decreasing

What is speed?

| Velocity | (absolute value of velocity)

When is a particle speeding up?

When acceleration and velocity have the same sign

When is a particle slowing down?

When acceleration and velocity have opposite signs

What is the derivative of an exponential (2 equations)

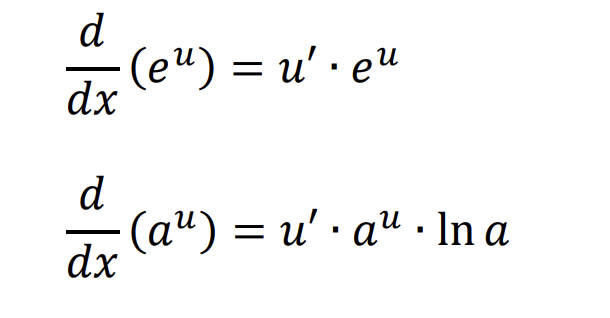
What is the derivative of a logarithmic (2 equations)

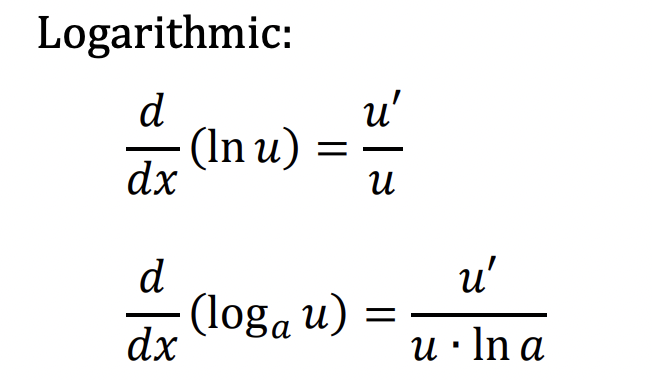
What is the extreme value theorem (EVT)

When f is continuous on the closed interval [a,b] f has an absolute minimum and an absolute maximum

How do you use EVT to find the absolute minimum and maximum

1. Find the critical point of f on interval (a,b)

2. Evaluate f at the critical points and at the endpoints x =a and x= b

3. The largest value is the absolute maximum and the smallest value is the absolute minimum

What is the mean value theorem (MVT)

If f(x) is continuous on the closed interval [a,b] and differentiable on interval (a,b) and exists at x = c on interval (a,b) then (equation in pic)

What is Rolle’s Theorem

If f(x) is continuous on the closed interval [a,b] and differentiable on interval (a,b) AND f(a) = f(b) and xists at x = c on interval (a,b) then (equation in pic)

L’Hopital’s Rule