exponentials and logarithms

what is the equation for a polynomial graph?

y = axⁿ

what is the equation for a exponential graph?

y = ab^x

what does a polynomial graph look like?

any graph with x to a degree, excluding x¹ because that’s a linear graph

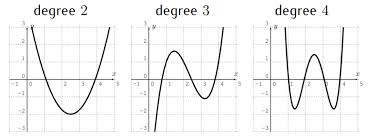
why isn’t a straight line graph considered a polynomial graph?

because it’s a linear graph. you don’t need to convert it using logs because it is already linear

what does an exponential graph look like?

y = 2x example

• asymptote at x = 0

• y - int = 1

• tends to towards 0 as x decreases

• grows without limit as x increases

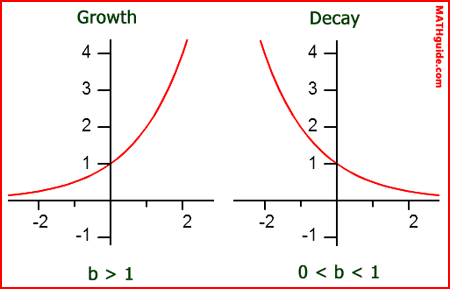
why is the y-int of an untransformed exponential graph always 1?

any value raised to the power of 0 is 1, and since x = 0 at the y-int, the y-int = 1

when is an exponential graph increasing (exponential growth)?

when k > 1

when is an exponential graph decreasing (exponential decay)?

when k < 1

why do we turn polynomial and exponential graphs into linear?

to be able to read the data clearly

polynomial → linear equation comparison

here

what is the y value for a polynomial graph turned linear?

log y

what is the gradient for a polynomial graph turned linear?

n

what is the x value for a polynomial graph turned linear?

log x

what is the y-int (c) for a polynomial graph turned linear?

log a

what is the y value for an exponential graph turned linear?

log y

what is the gradient for an exponential graph turned linear?

log b

what is the x value for an exponential graph turned linear?

x

what is the y-int (c) for an exponential graph turned linear?

log a

exponential → linear equation comparison

here

what are the similarities and differences between polynomial and exponential graphs turned linear?

similarities

• y = log y

• c = log a

differences

for a polynomial graph;

• gradient = n

• x = log x

for an exponential graph;

• gradient = log b

• x = x

which graph turned linear has a gradient of n?

polynomial

which graph turned linear has an x value of log x?

polynomial

which graph turned linear has a gradient of log b?

exponential

which graph turned linear has an x value of x?

exponential

which graph turned linear has a y value of log y?

both - polynomial and exponential

which graph turned linear has a c value of log a?

both - polynomial and exponential

what does e^kx integrate to?

ke^kx

what does e^kx differentiate to?

ke^kx

log_an = ?

log_an = x

a^x = ?

a^x = n

when a is not equal to 1

when is a^x = n valid?

when a doesn’t equal 1

how do we rewrite logs?

log_an = x

a^x = n

what are the logarithm laws?

1. multiplication law

log_ax + log_ay = log_axy

2. division law

log_ax - log_ay = log_ax/y

3. power law

log_a(x^k) = klog_ax

what is the multiplication law?

log_ax + log_ay = log_axy

log_ax + log_ay = ?

log_ax + log_ay = log_axy

what is the division law?

log_ax - log_ay = log_ax/y

log_ax - log_ay = ?

log_ax - log_ay = log_ax/y

what is the power law?

log_a(x^k) = klog_ax

log_a(x^k) = ?

log_a(x^k) = klog_ax

what are the special cases for logs?

• log_a (1/x) = log_a(x^-1) = -log_ax (power law when k = -1)

• log_aa = 1 (a > 0, a doesn’t = 1)

• log_a1 = 0 (a > 0, a doesn’t = 1)

what is the power law when k = -1?

log_a (1/x) = log_a(x^-1) = -log_ax

log_aa = ?

log_aa = 1

when is log_aa = 1 applicable?

(a > 0, a doesn’t = 1)

when is log_a1 = 0 applicable?

(a > 0, a doesn’t = 1)

when is log_a (1/x) = log_a(x^-1) = -log_ax applicable?

when k = -1

log_a1 = ?

log_a1 = 0

can you take a log of a negative number?

no

f(x) = g(x),

log_af(x) = ?

log_af(x) = log_ag(x)

what does the graph of y = ln x look like?

• a reflection of the graph y = e^x in the line y = x

• goes through (1, 0)

• doesn’t cross the y-axis

• y-axis asymptote of y = ln x, meaning ln x only defined for positive x values

• ln x slowly increases without limit as x increases

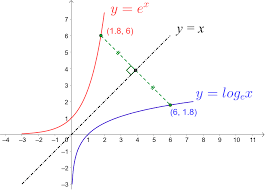
what is y = e^x an asymptote to?

x-axis

what is y = ln x an asymptote to?

y-axis

what is the x-axis asymptotic to?

y = e^x , exponential graph

what is the y-axis asymptotic to?

y = ln x , logarithmic graph

In x = ?

In x = log_ex

e^{ln x} = ?

e^{ln x} = ln (e^x) = x

how do we reverse e functions?

how do we reverse log functions? base of e, base of 10, base of a (i.e., another number)

if the graph y = e^x has a y-int of 1 (standard exponential graph), what is the x-int of the y = ln x graph? why?

(1,0), because the y = ln x graph is a reflection of the y = e^x graph in the line y = x

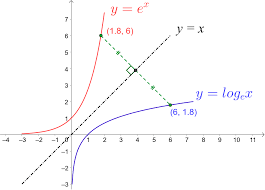
what is an exponential function?

f(x) = a^x , where a is a constant

what determines how steep an exponential graph is?

the size of it’s ‘a’ value -

• for increasing graphs, the larger the more steep

• for decreasing graphs, the smaller the more steep?

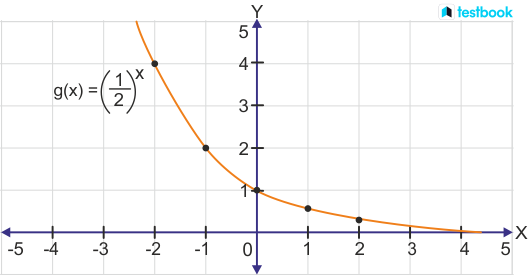
what does the untransformed graph of the function y = (1/2)^x look like?

• decreasing

• y-int at (0,1)

• reflection of y = 2^x in the y-axis

what does the graph of the function y = (1/2)^x-3 look like?

• f(x) = (1/2)^x , so y = f(x - 3)

• translation by vector (3, 0), i.e., +3 to x value

• to find y-int, substitute x = 0 (x value at y-intercept) into function

• y = (1/2)^0-3 = 8. y-int = (0, 8)

how do you turn a polynomial graph to a linear one?

1. start with non linear relationship, y = axⁿ

2. take log 10 of both sides

3. use multiplication law

4. use power law

5. compare to straight line equation;

   log y = n log x + log a

   y = m x + c

how do you turn an exponential graph to a linear one?

1. start with non linear relationship, y = ab^x

2. take log 10 of both sides

3. use multiplication law

4. use power law

5. compare to straight line equation;

   log y = log b x + log a

   y = m x + c

why is the integral and differential of an exponential graph y = ke^kx?

because exponential functions of the form f(x) = a^x have a special mathematical property that means their f’(x) and f(x) functions are a similar shape to each other. when a = e, the gradient and original function are identical

what is ‘e’?

a value of ‘a’, approximately 2.72, (3 s.f) where the gradient function is exactly the same as the original function

how do you sketch the graph y = e^2x ?

here 14.2 example 4 a

how do you sketch the graph y = 10e^-x ?

here 14.2 example 4 a

how do you sketch the graph y = 3 + 4e^(1/2)x ?

here 14.2 example 4 c

how do you sketch an exponential graph?

here

what is proportional in exponential modelling?

• for e^x, the rate of increase ∝ the value of the situation being modelled

• for e^-x, the rate of decrease ∝ the value of the situation being modelled

what does ‘solving’ a exponential mean?

finding the unknown value, usually x

what is a logarithm?

the inverse of exponential functions

what is ‘a’?

the logarithm base

negative y, flipped in x-axis

how to solve mixed exercise 3a and b, rewriting as a given function

how to solved mixed exercise 5a, rewriting into quadratics using substitutions

how to answer mixed exercise 8d, raising e to the power of 0

mixed exercise 8e, ask zanas

mixed exercise 9d, does it always tend towards 0 when t tends to infinity? ask

mixed exercise 9e, what does graph look like? why is it asymptotic at 100?

mixed exercise 9f appropriation of graph

mixed exercise 10a, writing straight line graph

why can time be ≥ 0?

time cannot be negative because you can’t go back in time

mixed exercise 11d

how do you answer this question?

mixed exercise 13a

mixed exercise 13c

mixed exercise 14c, writing in the right unit

the whole challenge.. ask someone cuz i dont fucking know

exercise 14g 4

exercise 14g 5d

how can you tell where the asymptote is on an equation?

y = Ae^Bx + C

C is where the asymptote is

14g challenge, how do we know it goes through the origin?

how do you solve this 14g 1a, solving equations

exercise 14g 4, exact solution means leave it in ln2? ask someone

can you have a log base 0?

no !!!

14d 6a how do you answer this

14d 7b justify why log_aa = 1

what are some assumptions we can give for exponential modelling?

1. assumes the growth / decay is exponential

2. other factors would affect population size over time

3. goes out of the range

what is the ‘long term prediction’ for exponential modelling?

as t → ∞, e^t → 0, therefore e value = 0