Chapter 17: Sampling Distribution Models

What is a sampling distribution?

A model of a statistic (like a sample mean or proportion) based on repeated samples from the same population.

What does the Central Limit Theorem (CLT) say?

For large samples, the sampling distribution of the sample mean becomes approximately Normal, regardless of the population’s shape.

When can we use the CLT for sample means?

• When the population is Normal

• Or when n ≥ 30 (large sample size)

What is the mean of the sampling distribution of the sample mean (\bar{x})?

  \mu_{\bar{x}} = \mu — the population mean

What is the standard deviation of the sampling distribution of the sample mean?

  \sigma_{\bar{x}} = \frac{\sigma}{\sqrt{n}}

Only valid if the sample is random and n \leq 10\% of population.

What is the sampling distribution of a sample proportion (\hat{p}) centered at?

  \mu_{\hat{p}} = p — the population proportion

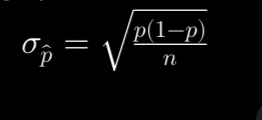
What is the standard deviation of \hat{p}?

What are the conditions for the Normal model for \hat{p}?

• Random sample

• 10\% condition: sample ≤ 10% of population

• Success/Failure condition: np \geq 10 and n(1-p) \geq 10

What are the 3 big ideas in sampling distribution models?

1. Center: Sampling distribution is centered at population value

2. Spread: Gets smaller as n increases

3. Shape: Becomes Normal if conditions are met

How does increasing sample size affect standard deviation?

It decreases the standard deviation — more data = less variability

Why is the 10% condition important?

It ensures independence when sampling without replacement

What’s the “Success/Failure” condition used for?

To check if it’s safe to model a sampling distribution of proportions using a Normal model