Propositional Logic, Connectives, and Quantifiers in Logic

Propositions

The basic building blocks of logic.

Example of a Proposition

Washington, D.C., is the capital of the United States of America.

Propositional Variables

We use letters to denote propositional variables (statement variables).

Conventional Letters for Propositional Variables

The conventional letters used for propositional variables are p, q, r, s.

Truth Value of a Proposition

The truth value of a proposition is true, denoted by T, if it is a true proposition.

Propositional Logic

The area of logic that deals with propositions is called the propositional calculus or propositional logic.

Historical Development of Logic

Propositional logic was first developed systematically by the Greek philosopher Aristotle more than 2300 years ago.

Disjunction

The use of the connective or in a disjunction corresponds to one of the two ways the word or is used in English, namely, as an inclusive or.

Truth of a Disjunction

A disjunction is true when at least one of the two propositions is true.

Conditional Statements

Statements of the form 'if p, then q' or 'p implies q'.

Converse of a Conditional Statement

The converse of p → q is q → p.

Contrapositive of a Conditional Statement

The contrapositive of p → q is ¬q → ¬p.

Inverse of a Conditional Statement

The inverse of p → q is ¬p → ¬q.

Equivalent Propositions

When two compound propositions always have the same truth value we call them equivalent.

Biconditionals

Another way to combine propositions that expresses that two propositions have the same truth value.

Implicit Use of Biconditionals

Biconditionals are not always explicit in natural language.

Logical Connectives

Four important logical connectives are conjunctions, disjunctions, conditional statements, and biconditional statements.

Bit

A bit is a symbol with two possible values, namely, 0 (zero) and 1 (one).

Boolean Variable

A variable that can take on the values of true or false.

Bit String

A bit string is a sequence of zero or more bits.

Length of a Bit String

The length of this string is the number of bits in the string.

Boolean Searches

Searches of large collections of information that employ techniques from propositional logic.

Logic Puzzles

Puzzles that can be solved using logical reasoning.

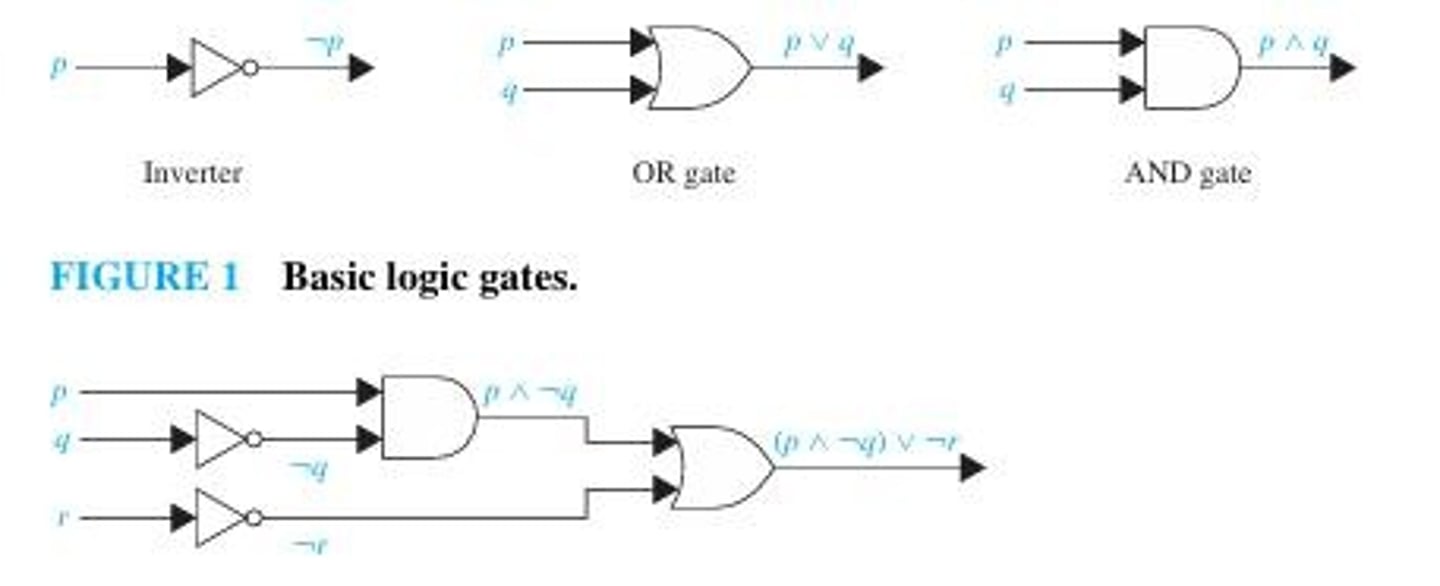
Logic Circuit

A logic circuit receives input signals p1, p2,..., pn, each a bit, and produces output signals s1, s2,..., sn, each a bit.

Basic Circuits (Gates)

The three basic circuits are Inverter (NOT Gate), OR Gate, and AND Gate.

Tautology

A compound proposition that is always true, no matter what the truth values of the propositional variables that occur in it.

Contradiction

A compound proposition that is always false.

Contingency

A compound proposition that is neither a tautology nor a contradiction.

Logically Equivalent

Compound propositions that have the same truth values in all possible cases.

De Morgan's Laws

The two logical equivalences known as De Morgan's laws are particularly important.

Compound Proposition

A compound proposition is satisfiable if there is an assignment of truth values to its variables that makes it true.

Unsatisfiable Proposition

A compound proposition is unsatisfiable when it is false for all assignments of truth values to its variables.

Sudoku Puzzle

A Sudoku puzzle is represented by a 9×9 grid made up of nine 3×3 sub grids, known as blocks.

Givens

The 81 cells in a Sudoku puzzle are called givens.

Predicate

A statement involving variables, such as 'x>3', 'x=y+3', 'x+y=z', or 'computer x is under attack by an intruder'.

Propositional Function

The statement P(x) is the value of the propositional function P at x.

Truth Value

Once a value has been assigned to the variable x, the statement P(x) becomes a proposition and has a truth value.

Predicate Calculus

The area of logic that deals with predicates and quantifiers.

Universal Quantifier ( ∀ )

Symbol: ∀x P(x). Meaning: 'For all x, P(x) is true.' True if P(x) holds for every element in the domain.

Counterexample

A universal quantifier statement is false if at least one counterexample exists.

Example of Universal Quantifier

'All humans are mortal' → ∀x (Human(x)→Mortal(x)).

Existential Quantifier ( ∃ )

Symbol: ∃x P(x). Meaning: 'There exists an x such that P(x) is true.' True if P(x) holds for at least one element in the domain.

Negating Universal Quantifier

¬(∀x P(x))≡∃x (¬P(x)).

Negating Existential Quantifier

¬(∃x P(x))≡∀x (¬P(x)).

Nested Quantifiers

Quantifiers can be combined, and the order matters (generally not interchangeable).

Example of Nested Quantifiers

∀x∃y P(x,y): For every x, there exists some y such that P(x,y).

Another Example of Nested Quantifiers

∃y∀x P(x,y): There exists a single y such that for every x, P(x,y).

Negating Quantifiers Rule

'It is not the case that all are ...' ↔ 'Some are not ...'.

Truth Dependence

Truth depends on the domain of discourse.

Example of Predicate

Example: P(x): x > 3.

Quantification

An important way to form propositions using predicates.