Chapter 8: Truth Tables Exercises (Symbolic Logic)

truth table

a table that records every combination of truth values we can assign to the simple statements in an argument

• used to test arguments

• used to classify statements

• used to classify pairs of statements

What are truth tables used for?

truth table definition for negation

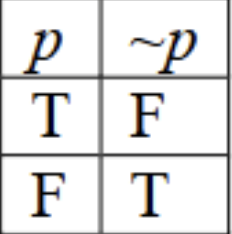
truth table definition for conjunction

truth table definition for disjunction

truth table definition for conditional

truth table definition for biconditional

The truth value of the main operator of any compound statement is determined (can be computed) by the truth values assigned to the simple statements in it

What does it mean to say that the truth value of any compound statement is a function of the truth values assigned to its simple components?

true

• disjunctive statements are true when at least one disjunct is true

Assume that A and B are true, that C and D are false, and that X and Z have unknown truth values.

Indicate whether the given statement is true, false, or has an undetermined truth value:

B ∨ Z

undetermined

• can only determine true if both conjuncts are true

Assume that A and B are true, that C and D are false, and that X and Z have unknown truth values.

Indicate whether the given statement is true, false, or has an undetermined truth value:

A ● X

false

• because true antecedent and false consequent

Assume that A and B are true, that C and D are false, and that X and Z have unknown truth values.

Indicate whether the given statement is true, false, or has an undetermined truth value:

A ⊃ (B ● C)

true

• because at least one disjunct is true

Assume that A and B are true, that C and D are false, and that X and Z have unknown truth values.

Indicate whether the given statement is true, false, or has an undetermined truth value:

A ∨ [Z ⊃ (B ⊃ ∼C)]

false

• idk why tbh

Assume that A and B are true, that C and D are false, and that X and Z have unknown truth values.

Indicate whether the given statement is true, false, or has an undetermined truth value:

B ≡ (D ∨ ∼A)

true

• because consequent is true

Assume that A and B are true, that C and D are false, and that X and Z have unknown truth values.

Indicate whether the given statement is true, false, or has an undetermined truth value:

[X ∨ (∼A ≡ D)] ⊃ B

false

• because the tilde negates the true statement

Assume that A and B are true, that C and D are false, and that X and Z have unknown truth values.

Indicate whether the given statement is true, false, or has an undetermined truth value:

∼[B ● ∼(C ∨ D)]

false

• because there will be different truth values regardless

Assume that A and B are true, that C and D are false, and that X and Z have unknown truth values.

Indicate whether the given statement is true, false, or has an undetermined truth value:

Z ≡∼Z

true

• because both conjuncts are true

Assume that A and B are true, that C and D are false, and that X and Z have unknown truth values.

Indicate whether the given statement is true, false, or has an undetermined truth value:

B ● (D ⊃ A)

true

• if a statement is true, then every other statement implies it

Assume that A and B are true, that C and D are false, and that X and Z have unknown truth values.

Indicate whether the given statement is true, false, or has an undetermined truth value:

X ⊃ (A ⊃ X)

1. Count the number of different letters (let that = n)

2. Compute 2ⁿ = total number of lines in truth table

3. Divide total number of lines in half; start with the leftmost letter and fill in that many trues and falses alternating to the bottom everywhere this letter appears

4. Divide in half again; go to the leftmost letter and fill in this number of trues and falses alternating to the bottom everywhere this letter appears

5. Fill in the values for each operator.

6. Check to see whether, on any line, all the premises are true and the conclusion is false.

   1. If yes, the argument is invalid.

   2. If no, the argument is valid.

How is a truth table used to determine whether an argument is valid?

True

• this makes it an EFFECTIVE method

True or False:

For any argument in propositional logic, the truth table method (unlike the method of counterexample) is guaranteed to produce a definite result (valid, invalid) in a finite number of mechanical steps if used correctly.

Valid

• No matter what truth values are assigned to P and Q, the argument NEVER has TRUE premises and a FALSE conclusion.

  • AKA: there is no line that has 2 T premises and a F conclusion

• Consult Pictures on Phone for Work

Test the argument below for validity using a truth table: 

1. P ∨ Q

2. ∼P

3. So, Q

Invalid

• both premises are true and the conclusion is false

• Consult Pictures on Phone for Work

Test the argument below for validity using a truth table: 

1. P ⊃ Q

2. ∼P

3. So, Q

Valid

• no line w/ a true premise and a false conclusion

• Consult Pictures on Phone for Work

Test the argument below for validity using a truth table: 

1. P ∨ (Q ● P)

2. So, P

Invalid

• both premises are true and the conclusion is false

• Consult Pictures on Phone for Work

Test the argument below for validity using a truth table: 

1. P ● Q

2. Q ⊃ R

3. So, ∼R

Valid

• no line with a true premise and false conclusion

• Consult Pictures on Phone for Work

Symbolize this argument and test it for validity using a truth table:

If Smith wins the election, then I’ll eat my hat. So, if I don’t eat my hat, then Smith didn’t win the election.

Valid

• because no line with a true premise and false conclusion

• Consult Pictures on Phone for Work

Symbolize this argument and test it for validity using a truth table:

This is gold if, and only if, its atomic number is 79. So, it’s being gold implies that its atomic number is 79, and its atomic number being 79 implies that it’s gold. 

tautology

a statement that is necessarily true

• could not possibly be false

Every line under the main operator is true

tautology in truth table terms

self-contradictory statement

a statement that is necessarily false

Every line under the main operator is false.

self-contradictory statement in truth table terms

contingent statement

a statement that is neither necessarily true nor necessarily false

There’s at least one line under the main operator on which the main operator is true andat least one on which its false. 

truth table terms in contingent statement

tautology

• because there’s a T under the main operator on every line. 

• Consult Pictures on Phone for Work

If a statement is true, everything implies it

Use a truth table to classify this statement:

X ⊃ (A ⊃ X)

Contingent

• because at least one line where the main operator is true and at least one where it’s false. 

• Consult Pictures on Phone for Work

Use a truth table to classify this statement:

K ⊃ (K ≡ ∼L)

Self-Contradictory Statement

• because every line under the main operator is false

• Consult Pictures on Phone for Work

Use a truth table to classify this statement:

[∼B ● (B ∨ ∼A)] ● A

tautology

• because every line under the main operator is true

When you negate a self-contradiction, the result must be a tautology.

Use a truth table to classify this statement:

∼(R ● ∼R)

The statements have the same truth value under the main operators on every line.

truth table terms of equivalent statements

The statements have the opposite truth value under the main operators on every line. 

truth table terms of contradictory statements

There is at least one line where both statements have true main operators.

truth table terms of consistent statements

There is no line where both statements have true main operators.

truth table terms of inconsistent statements

a. = A)

b. = B)

c. = C)

d. = D)

Consult Pictures on Phone for Work

Use a truth table to put each pair of statements below into one of these categories:

A) Consistent, but not logically equivalent

B) Logically Equivalent

C) Inconsistent, but not contradictory

D) Contradictory

a. C ≡ D, and ∼D ⊃ C

b. ∼(R ● S), and ∼R ∨ ∼S

c. P ≡ Q, and P ● ∼Q

d. P ∨ Q, and ∼(Q ∨ P)

True or False:

If an argument’s conclusion is a tauology, then the argument must be valid. 

True or False:

If two statements are logically consistent with one another, then each will validly entail the other. 

Consider the valid argument below:

1. P ⊃ Q

2. P

3. So, Q

Now consider the statement:

[(P ⊃ Q) ● P] ⊃ Q]

If we were to construct a truth table to categorize this statement, what kind of statement would it be?

Test the argument below using an indirect truth table:

1. P ⊃ Q

2. Q

3. So, P

Test the argument below using an indirect truth table:

1. P ⊃ Q

2. ∼Q ● ∼R

3. So, ∼P

Test the argument below using an indirect truth table:

1. P ∨ (Q ● P)

2. So, P

equivalent

two statements that MUST have the SAME truth value

contradictory

two statements that MUST have OPPOSITE truth values

consistent

two statements that CAN be true simultaneously

inconsistent

two statements that CAN’T be true simultaneously