Pre-Calc - Inverse Trig Functions Graphing and everything about graphing them and Inverses in general

Inverse Functions

An inverse function is a function that “undoes” the action of another function.

In other words, if you have a function F(x) that takes an input x and gives an output y, its inverse f^-1(x) takes y and returns the original x.

✅ Example:

• f(x)=3x+2

• f^-1(x)=(x−2)/3   to get this change x and y in orginal equation and solve for y 

So f(f^-1(x))=x and f^-1(f(x)=x

Inverse functions GRAPHING VERY IMPORTANT

THEY ARE THE reflection of the original function across the line y = x. SO CHECK IT

Inverse properties of trig functions

Inverse Trig Functions Properties

For any angle in the restricted domain of the inverse function:

sin⁡(arcsin(x))=x for x∈[−1,1] and arcsin(siny)

Similarly:

cos⁡(arccos(x))=x, arccos(cos⁡(x))=x x∈[0,π]

tan⁡(arctan(x))=x arctan⁡(tan⁡(x))=x. x∈(−π/2,π/2)

How to check if a function has an inverse

Use the horizontal line test if every horizontal line intersects the graph at most once, the function is one-to-one and has an inverse.

what does arc mean

It is the inverse just written in a different way

like arcsin means inverse function of sine

What do inverse functions do

They let you find the angle θ given a trig value.

Example: If sin θ = 1/2, then θ = arcsin(1/2) = π/6 or 30° (within the restricted domain).

EX from notes 

arcsin(sintheta)=arcsin 3/5

means that what angle has a value of SINE that = 3/5

Graphing for all

All the key points like for arccos(x) the key points for cos(x) is Identify key points on the restricted cosine graph:

Find a few key points on this restricted graph. Some examples are:

(0,1), (π/2,0), (π,-1)

Then Swap the x and y coordinates: To find the corresponding points on the inverse function's graph, swap the x and y values for each point.

(0,1) becomes (1,0)

(π/2,0) becomes (0,π/2)

(π,-1) becomes (-1,π)

Arcsin

Sin does not have inverse, does not pass horizontal line test, not a one-to-one function. 

HOWEVER, IF YOU RESTRICT DOMAIN TO (-pie/2 to pie/2) then is a one-to-one.

THEN, to get inverse reflect over y=x AKA just switch the domain and rangle and make the Domain the range and the range the domainsolve

Domain: [-1, 1]

Range: [-pi/2, pi/2]

This means that the range can only be in quadrant 1 or 4 the range is usually the angle in radians

The domain is the input, usually one of the values of cos or sin on the unit circle. 

• Table for graphing arcsin x

• _____

• y=-pie/2 - x=sin y is -1 

• y=-pie/4 - x=sin y is -root2/2

• y=-pie/6 - x=sin y is  -1/2

• y=0 - x=sin y is 0

arccos

Range restriction for cosine (-1,1) and Domain restriction for cosine (0, pie). 

This means the angle in radians can only be in the first 2 quadrant

THEY ARE RESTRICTED ABOVE BECAUSE THAT IS THE RESTRICTION NEEDED TO BE ONE-TO ONE

Domain: [-1,1]

Range: [0,pi]

arcsec

Domain: (-∞, -1] [1, ∞)

Range: [0, π/2) (π/2, π]

arccsc

Domain: (-∞, -1] [1, ∞)

Range: [-π/2, 0) (0. π/2)

arctan

Domain: (-infinity, infinity)

Range: (-pi/2, pi/2)]

Means that the range (the angle in radians) is first or second quadrant

arccot

Domain: (-∞, ∞)

Range: (0, π)

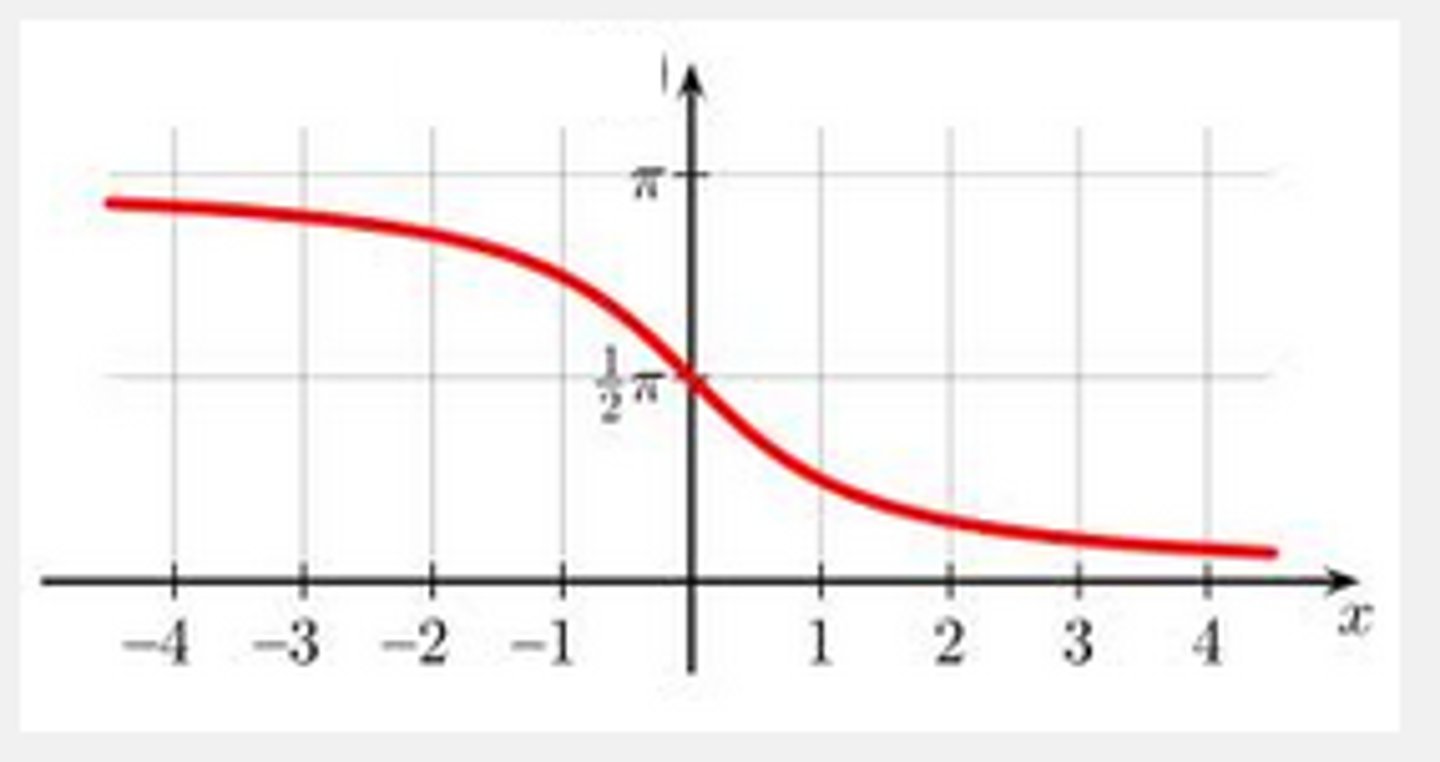
Overall table for all

Function	Domain of original	Range of inverse	Notes
sin	[-π/2, π/2]	[-1, 1]	arcsin(x) only gives angles in [-π/2, π/2]
cos	[0, π]	[-1, 1]	arccos(x) only gives angles in [0, π]
tan	(-π/2, π/2)	(-∞, ∞)	arctan(x) only gives angles in (-π/2, π/2)
csc	[-π/2, 0) ∪ (0, π/2]	(-∞, -1] ∪ [1, ∞)	arccsc(x) restricted to avoid 0
sec	[0, π/2) ∪ (π/2, π]	(-∞, -1] ∪ [1, ∞)	arcsec(x) restricted to avoid π/2
cot	(0, π)	(-∞, ∞)	arccot(x) gives angles in (0, π)

Example problems

y=2arccosx

y=arctan2x

y=pie/2+arctanx