DSA (Midterms)

Binary Tree

• allows data to be organized hierarchically, making it valuable in scenarios where data relationship exists.

• it can have up to two (2) child nodes per parent.

Root node

Topmost mode of this tree

two (2)

Every parent node may have only __ children (left/right child)

Data Element

Functions as a storage for the data value that the node needs to store

Pointer to the Left Child

holds the address to the left child node.

Pointer to the Right Child

holds the address to the right child node.

Tree Traversal

• process of visiting every node in a tree exactly once in a particular order to access or process data.

• Breadth-First Traversal

• Depth-First Traversal

two (2) primary types of tree traversal

Breadth-First Traversal

• also known as Level Order Traversal

• visits the nodes level by level from the root downwards, moving horizontally across each level before descending to the next.

Depth-First Traversal

the traversal proceeds by exploring as deeply as possible along each branch before backtracking.

Inorder Traversal

• LVR

• This method is particularly useful in binary search trees because it retrieves values in a naturally sorted order.

Preorder Traversal

• VLR

• Commonly applied in tasks such as creating a duplicate of the tree or evaluating prefix expressions.

Postorder Traversal

• LRV

• useful when a task requires processing child nodes before their parent node (safely deleting a tree/evaluating postfix expression).

Binary Search Tree

• used for retrieving, sorting, and searching data.

• Ordered Binary Tree

duplicate keys

BSTs do not allow _____________ because the rule of being left being less and right being greater would be broken. Each key must appear only once.

O(log n)

Each node’s key is unique in the entire tree, ensuring efficient search, insert, and delete operations with a time complexity of _______.

Adelson-Velskii Landis (AVL)

is a self-balancing BST in which each node maintains extra information called a balance factor whose value is either -1, 0, or 1.

Balance Factor = Height (Left Subtree) - Height (Right Subtree)

rotations

• if the balance factor goes beyond -1 or +1, the tree self-balances using ________.

• whenever an insertion/deletion operation causes a node’s balance factor to go beyond -1 or +1, it is applied to restore balance.

Left-Left Rotation

• insertion happens in the LEFT subtree of the LEFT child.

• A  > B > C

• right rotate A

• after B root

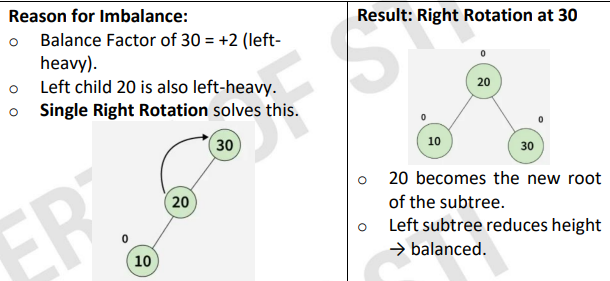
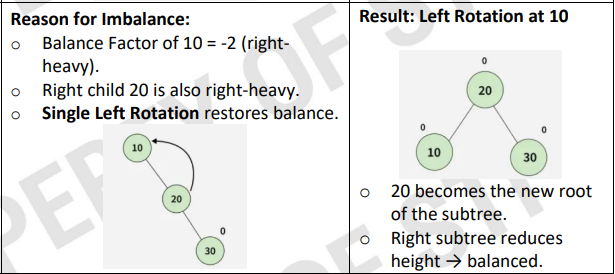
Right-Right Rotation

• insertion happens in the RIGHT subtree of the RIGHT child.

• A < B < C

• left rotate A

• after B root

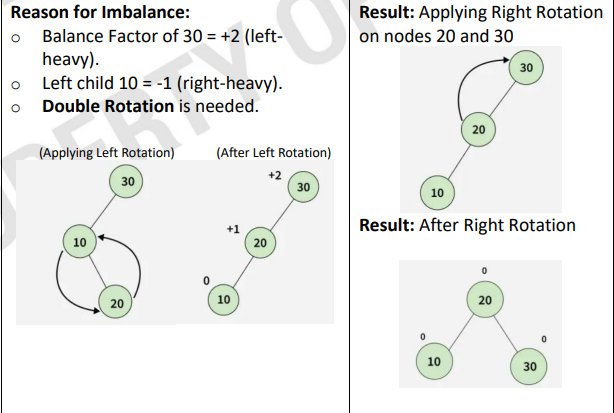
Left-Right Rotation

• insertion happens in the RIGHT subtree of the LEFT child (zig-zag).

• A > B < C

• left rotate B, right rotate A

• after C root

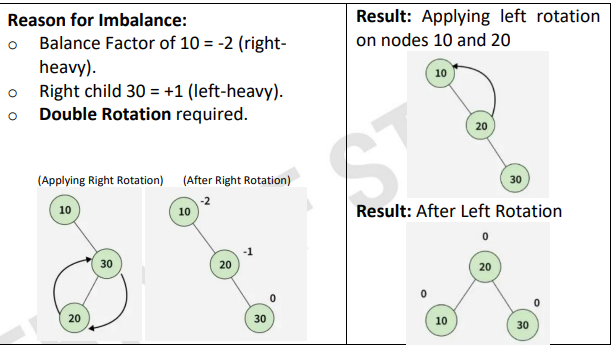
Right-Left Rotation

• insertion happens in the LEFT subtree of the RIGHT child.

• A < B > C

• right rotate B, left rotate A

• after C root

Application of Trees

trees are widely used in computer science due to their efficient representation of hierarchical relationships and their ability to optimize data operations.

Hierarchical Data Representation

• represents file systems (directories contain subdirectories & files in a tree-like format).

• DOM in HTML/XML docs use tree structures to illustrate nested relationships clearly.

Efficient Searching and Sorting

• BST, AVL, and Red-Black Trees provide fast access, insertion, and deletion operations.

• Ensures that these operations remain efficient (esp w/ frequent data updates).

Databases and File Storage Systems

• Relies heavily on tree structures (B- Trees & B+ Trees)

• used to manage large volumes of data and support efficient indexing & range queries (MySQL & Oracle)

• Tries (prefix trees)  are used for fast retrieval in applications such as autocomplete systems, dictionary lookups, & IP routing in networks.

AI & Game Development

• trees play a central role.

• decision trees are commonly used for classification problems in machine learning.

• minimax trees guide decision-making in competitive games like chess (optimized using alpha-beta pruning).

• Behavior trees widely used in modern video games to control NPC behavior in a structured and modular way.

Compiler Design

• rely on Abstract Syntax Trees (AST) to represent the syntactic structure of programming languages (parse and analyze code efficiently).

• Parse trees also help visualize the grammatical structures of code inputs.

Cryptography and Security

• Merkle Trees (blockchain technologies like BTC and ETH), facilitates fast and secure verification of transaction.

• Authentication systems also use the tree structures to organize & verify credentials efficiently.

Networking

• trees are essential for building routing tables and performing fast IP lookups using trie structures.

• Minimum Spanning Tree (MST), employed through Kruskal’s or Prim’s algo, are used to optimize network designs by minimizing connection costs.

Heap Data Structure

• binary tree in which every node is larger than the values associated with either child.

• largest/smallest value is always at the top (root) of the tree.

• Complete Binary Tree (Shape Property)

• Heap Order Property

Properties of Heap Data Structure (2 types)

If written, make sure to use a bullet form
(e.g.

• bonbon

• bantot

• magic

• kulit)

• Max-Heap

• Min-Heap

Types of Heap Data Structure (2 types)

If written, make sure to use a bullet form
(e.g.

• bonbon

• bantot

• magic

• kulit)

Max-Heap

• the parent node is always greater than/equal to its children.

• largest value is always at the root of the tree.

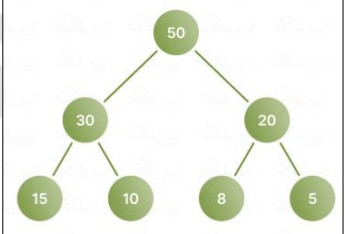
• Heapsort

• Priority Queues

• Top-K Tracking

Max-Heap use cases:

If written, make sure to use a bullet form
(e.g.

• bonbon

• bantot

• magic

• kulit)

Heapsort

(Max-Heap)

• comparison-based sorting algo that uses a binary heap to repeatedly extract the max/min element and place it at the end of array.

• it uses a max-heap to sort an array in ascending order by repeatedly extracting the max and placing it at the end.

Priority Queues (Max-Heap)

• element with the highest priority is accessed first, such as real-time operating systems (RTOS) and emergency resource allocation systems.

• put the “(Max-Heap)” at the end of your answer

Top-K tracking

• process of efficiently maintaining the K largest/smallest elements from a continuous stream/large dataset, without sorting the entire input.

• size of K is used to find the K smallest elements (max-heap). New elements are compared to the root (largest); if smaller value, it is replaced.

• applied in product-ranking systems (bottom K-scores) & real-time performance analytics (slowest transactions).

Min-Heap

• the parent node is always less than/equal to its children.

• smallest value is always at the root of the tree.

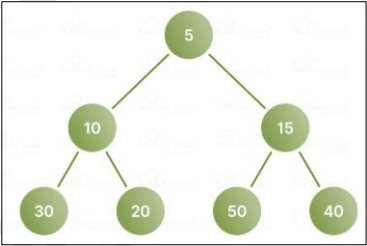
• Dijkstra’s Algorithm

• Priority Queues

• Event-Driven Simulations

Min-Heap use cases:

If written, make sure to use a bullet form
(e.g.

• bonbon

• bantot

• magic

• kulit)

Dijkstra’s Algorithm

• uses min-heap to extract the next closest vertex (smallest tentative distance).

• applied in GPS routing, network routing protocols & game AI pathfinding.

Priority Queues (Min-Heap)

• min-heaps are the backbone of priority queues (task with lowest cost are processed first).

• applied in CPU scheduling (shortest-job-first), task sched in OS, and printer job management.

• put the “(Min-Heap)” at the end of your answer.

Event-Driven Simulation

• stores and retries the next event based on the timestamp.

• min-heap ensures earlier event is always at the top.

• applied in network simulations, manufacturing process simulations, logistics & supply chain modeling.

Insert (Push)

adds a new element to the heap by adding it at the bottom

Extract Root (Pop)

removes and returns the root element with the last element

Peek (Get Root)

returns the root without removing it.

Replace

removes the root and inserts a new element in a single operation.

Heapify

• process of converting an arbitrary array (no specific structure/order) to a valid heap.

• heap property (parent >= or <= children) is maintained from a given node down to its descendants.

• Up-Heapify

• Down-Heapify

Two (2) heapify operations are:

If written, make sure to use a bullet form, answer must be complete.
(e.g.

• bonbon

• bantot

• magic

• kulit)

Up-Heapify (Bubble-Up)

• used after inserting a new element to restore the heap property by moving the element up the tree.

Down-Heapify (Bubble-Down)

• used after deleting the root element to restore the heap property by moving the new root element down the tree.

Priority Queues

• abstract data type that operates like a regular queue, except that each element priority level, and elements are dequeued based on their priority, not just their arrival order.

• elements with higher priority are processed first.

Implementing Priority Queues using Heaps

The standard approach is to use an array/ArrayList starting at position 1 (instead of 0), where each item in the array corresponds to one node in the heap.

• The root of the heap is always in array[1]

• its left child is in array[2]

• its right child is in array[3]

Implementing Insert

When a new value is inserted into a priority queue, add the value so that the heap still has its properties.

To achieve:

• Add the new value at the end of the array; that corresponds to adding it as a new rightmost leaf in the tree (or complete binary, all leaves were at the same depth) ensures that the heap has its shape property.

• Compare the new value in its parents to check. If the parent is smaller, swap the values until the order property holds/reaches the root.

Implementing removeMax

Due to order property, the largest value is always at the root. The removeMax operation will always remove & return the root values.

To achieve:

• Replace the value in the root with the value at the end of the array (corresponds to rightmost leaf at depth d).

• Remove that leaf from the tree.

• From down the tree, swap the values to restore the order property: each time is the value in the current node < one of its children, then swap its value with the larger child. Ensures that the new root value > both of its children.