Hypothesis testing part 1

hypotheiss testing

quantify observed difference

asses how likely it is that this differenced occured by chance alone

choose a critical value in terms of probability

e.g. 95% etc

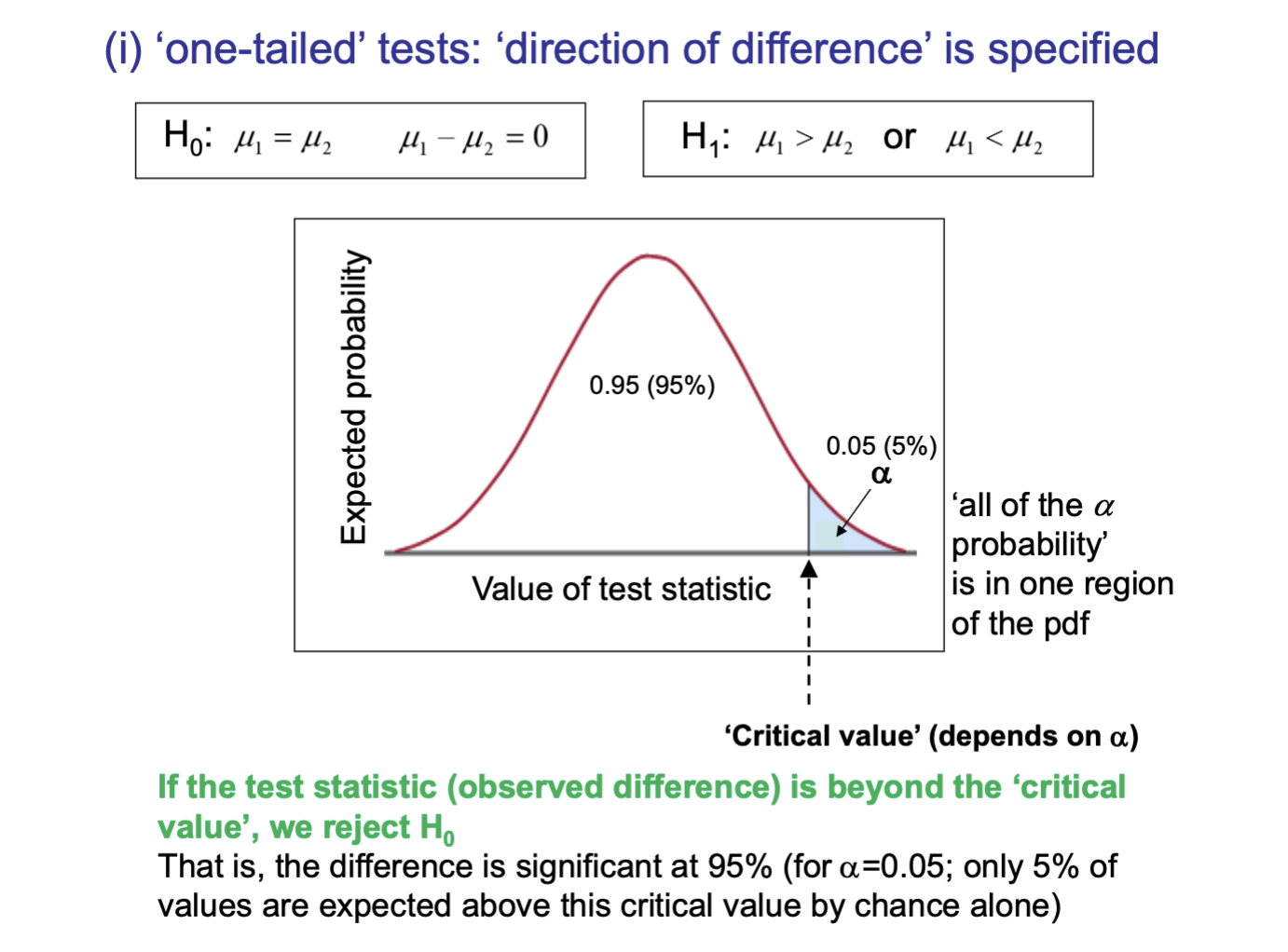
one tailed tests

direction of difference is specified

alpha is the area shaded in the graph / the bit we are looking at

rest of of the curve is the confidence level

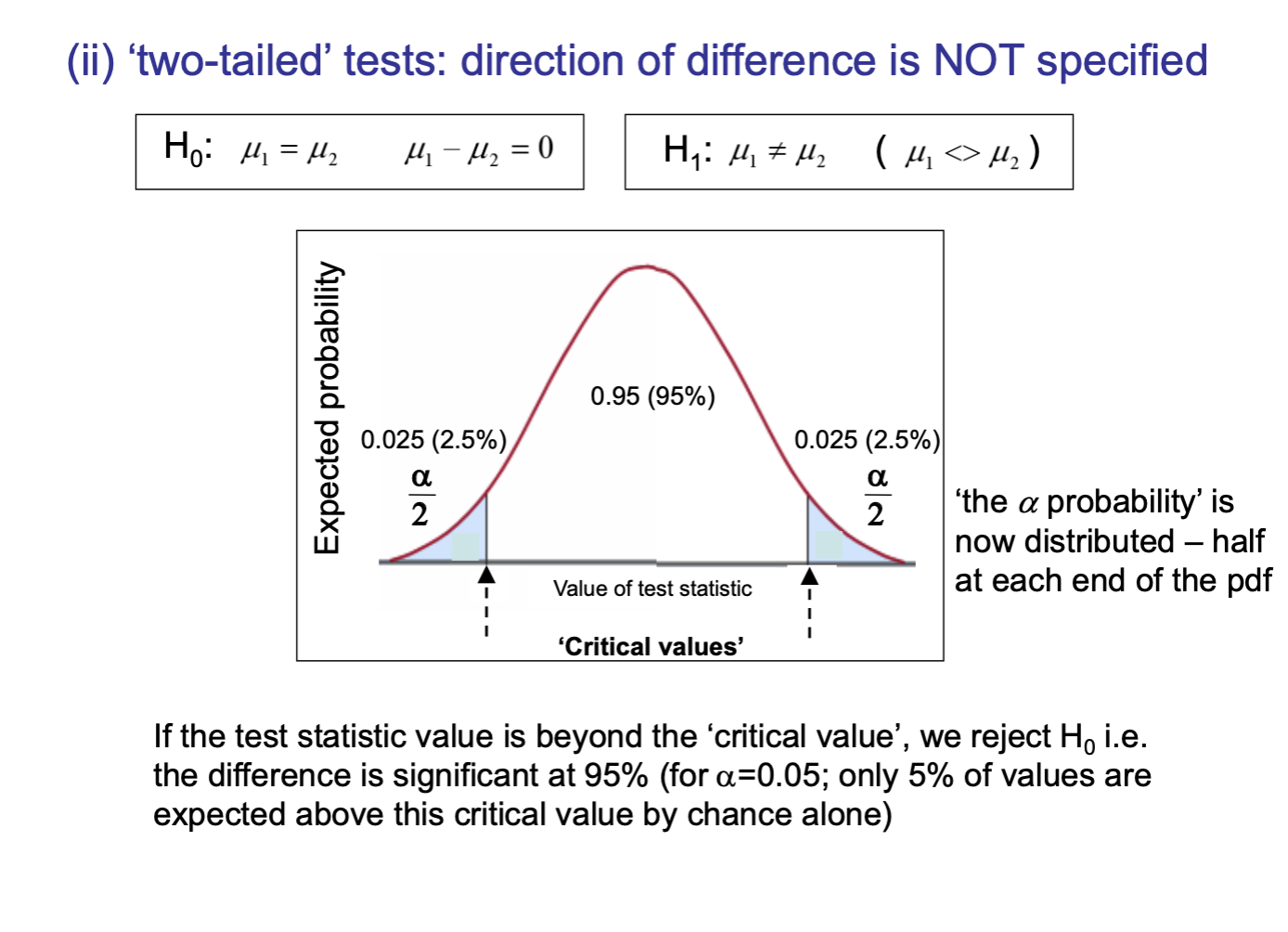
two tailed tests

direction not specified

alpha split in half

hypothesis test details

formulate null and alternative hypothesis

decide on significance level

select appropriate test

look up critical value - threshold for rejection null

if test is beyond the critical value reject null at a level of confidence equal to 1 - alpha in %

1 sample t test

compare a sample mean to a chosen value

2 sample t test

compare 2 means each from their won sample

smaller than 30 - will not be normal distribution

larger than. 30 - will roughly resemble normal distribution

equal or unequal variances ?

stds similar = equal variances

otherwise - use unequal variances

for this one do the sp formula first, then the t calc formula

then use the degrees of freedom formula

look up critical value

if t crit is greater than t calc - have evidence to reject null

calculate t statistic

for this one do the sp formula first, then the t calc formula using the value u get from the first formula

then use the degrees of freedom formula

remember in degrees of freedom to divide sample number by 2

compare the test statistic and the critical value

reject the null as a level of confidence equal to 100(1- alpha) of the t calc value is greater that the t critc value

type 1 error

rejecting null hypothesis which is true

is alpha is set too high

Type 2 error

failing to reject a null hypothesis which is true

ANOVA

comparing multipel samples

between 3 or more samples