AP Calc AB Formulas

sin²x + cos²x =

1

1 + tan²x =

sec^2 x

1 + cot²x =

csc^2 x

sin(A + B) =

sinA cosB + cosA sinB

sin(A - B) =

sinA cosB - cosA sinB

cos (A + B) =

cosA cosB - sinA sinB

cos (A - B)

cosA cosB + sinA sinB

sin(2x) =

2sinx cosx

cos(2x)

cos^2 x - sin^2 x

sin(-x) =

-sinx

cos(-x) =

cosx

tan(-x) =

-tanx

Definition of |x|

|x| = {
x if x >= 0
-x if x < 0

distance between two points

sqrt( (x2 - x1)^2 + (y2 - y1)^2 )

midpoint formula

((x1 + x2) / 2, (y1 + y2) / 2)

ln(ab) =

lna + lnb

ln(a/b) =

lna - lnb

ln(a^n) =

n * lna

ln(1/a) =

-lna

sec(x) =

1 / cos x

csc(x) =

1 / sin x

tan(x) =

sin x / cos x

cot(x) =

cos x / sin x

Definition of a limit

lim x -> a f(x) = L iff lim x -> a^- f(x) = L = lim x -> a^+ f(x)

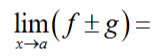
lim x -> a f +- lim x -> a g

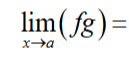
lim x -> a f * lim x -> a g

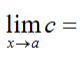
c

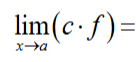
c * lim x -> a f

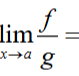
lim x -> a f / lim x -> a g for lim x -> a g != 0

Definition of Vertical Asymptote:

The line x = a is called a vertical asymptote iff lim x -> a^- f(x) = +-infinity or lim x -> a^+ f(x) = +-infinity

Definition of Horizontal Asymptote: (use “a” and f(x) to answer)

The line y = a is called a horizontal asymptote iff lim x -> -infinity f(x) = a or lim x -> infinity f(x) = a

Limits of the ratios of two functions

ln x < x^c < x^c * ln x < x^c+d < a^x < x! < x^x

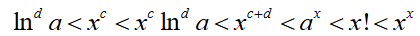
if f grows faster than g, then

lim x -> infinity
g(x) / f(x) = 0
f(x) / g(x) = infinity

Definition of continuity

a function f is continuous at x = a iff
1. f(a) exists
2. lim x -> a f(x) exists
3. lim x -> a f(x) = f(a)

Intermediate Value Theorem (IVT): If, then

If

1. f is continuous on the closed interval [a,b]

2. f(a) != f(b)

3. k is between f(a) and f(b)

Then there exists a number c between a and b for which f(c) = k

Squeeze Theorem

if f(x) <= g(x) <= h(x) and as x -> a, f(x) -> L and h(x) -> L, then g(x) -> L

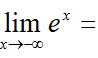
0

lim x -> infinity e^x =

infinity

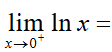
-infinity

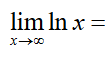
infinity

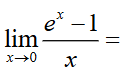
1

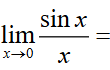
1

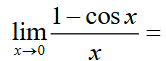
0

e^c = (2 equations of common limits)

lim x -> +- infinity (1 + c/x)^x
lim x -> 0^+ (1 + cx)^(1/x)

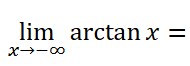
-pi / 2

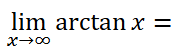
pi / 2

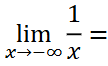
0

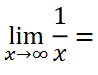
0

derivative standard formula/ limit of the difference quotient

f’(x) = lim h -> 0 ( f(x + h) - f(x) ) / h

Derivative alternative formula

f’(x) = lim x -> c ( f(x) - f(c) ) / (x - c)

Normal Line

The line perpendicular to the tangent line at the point of tangency.

Average rate of change of f from x = a to x = b is (definition and equation)

the slope of the secant line between the 2 points
( f(b) - f(a) ) / ( b - a )

average rate of change =

delta f / delta x
delta y / delta x
( f(b) - f(a) ) / (b - a)

Three reasons a function, f, will not be differentiable at a point x = a

1. f is not continuous at x = a

2. The graph of f has a “corner” or “cusp” at x = a

3. The graph of f has a vertical tangent at x = a

s(t) =

position

v(t) =

velocity = s’(t)

|v(t)| =

speed

a(t) = 

acceleration = v’(t) = s’’(t)

particle at rest when v(t) =

0

speed is increasing if

v and a have the same sign

speed is decreasing if

v and a have opposite signs

average velocity is the same as 

average rate of change of the position

differentiation rules

f and g are functions of x
c is a constant

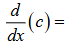
0

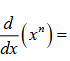
n * x^(n-1)

or d/dx [cf(x)] =

c * d/dx f(x)

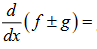
d/dx f(x) +- d/dx g(x)

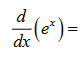
e^x

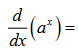
a^x * ln(a)

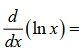
1/x

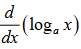
1/(x * lna)

Chain Rule: if h(x) = f(g(x), then

h’(x) = f’(g(x) * g’(x)

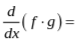
Product Rule

f’ * g + f g’

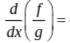
Quotient Rule

(f’ * g - f * g’) / g^2

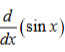
cosx

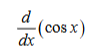
-sinx

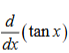
sec^2

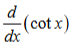
-csc^

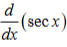
secx * tanx

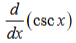
-cscx * cotx