Unit 1: Exploring One-Variable Data

AP Statistics | 2024-2025

What are statistics?

What are statistics?

the science and art of collecting, analyzing, and drawing conclusions from data

What is data analysis?

the process of collecting, analyzing, and drawing conclusions from data

What are individuals?

objects described in sets of data

What are variables?

attributes that can take different values for different individuals

What does a categorical variable do?

assigns labels that place each individual into a particular group, called a category

What does a quantitative variable do?

takes number values that are quantities

How do you tell whether a variable is categorical or quantitative?

if you can take the average of the variable, it’s quantitative, and if you can’t take the average, it’s categorical

What are examples of a categorical variable?

color, type, phone number, ID number

What are examples of a quantitative variable?

age, money, minutes, miles

What are we interested in when looking at variables?

the pattern of variation

What is distribution of a variable?

it tells us what values the variable takes and how often it takes those values

What should you do when analyzing data?

• examine each variable by itself, then study the relationships among the variables

• start with a graph, then add numerical summaries

What are descriptive statistics?

the process of explanatory data analysis

What are inferential statistics?

the process of drawing conclusions that go beyond the data at hand

What types of graphs are useful when analyzing a distribution?

bar graphs and pie charts

How do bar graphs work?

they compare several quantities by comparing the heights of bars that represent those quantities

Why should you draw the bars of a bar graph equally wide?

because our eyes react to width of bars as well as their heights

What should you keep in mind when analyzing data?

• beware pictographs

• watch the scales

When is it inappropriate to use a pie chart?

when data comes from different variables

What is a two-way table?

a table of counts that summarizes data on the relationship between 2 categorical variables for some group, organizing counts according to a row and a column

What does a marginal distribution do?

it gives the percent or proportion of individuals that have a specific value for one categorical variable

How do you examine a marginal distribution?

1. use the data in the table to calculate the marginal distribution (in percentages) of the row or column totals

2. make a graph to display the marginal distribution

What does a conditional distribution do?

it describes the values of that variable among individuals who have a specific value of another variable

How do you examine or compare conditional distributions?

1. select the row(s) or column(s) of interests

2. use the data in the table to calculate the conditional distribution (in percentages) of the row(s) or column(s)

3. make a graph to display the conditional distribution

   • use a side-by-side var graph or segmented bar graph to compare distributions

What is marginal relative frequency?

the percent or proportion of individuals that have a specific value for one categorical variable

What is joint relative frequency?

the percent or proportion of individuals that have a specific value for one categorical variable and a specific value for another one

What is conditional relative frequency?

the percent or proportion of individuals that have a specific value for one categorical variable among individuals who share the same value for another categorical variable

What is a side-by-side bar graph?

it displays the distribution of a categorical variable for each value of another categorical variable; bars are grouped together based on the values of one categorical variables and placed side by side

What is a segmented bar graph?

it displays the distribution of a categorical variable as segments of a rectangle, with the area of each segment proportional to the percent of individuals int he corresponding category

When does an association occur?

when knowing the value of one variable helps us predict the value of the other

What is a mosaic plot?

a modified segment bar graph in which the width of each rectangle is proportional to the number of individuals in the corresponding category

How does a dot plot display data?

it shows each value as a dot above its location on a number line

How do you make a dot plot?

1. Draw a horizontal axis and label it with the quantitative data

2. Scale the axis from the minimum to the maximum value

3. Mark a dot above the location on the horizontal axis corresponding to each data value

What should you always ask after making a graph?

“what do I see?”

When is a distribution roughly symmetric?

if the right and left sides of the graph are approximately mirror images of each other

When is a distribution skewed to the right?

if the right side of the graph is much longer than the left side

When is a distribution skewed to the left?

if the left side of the graph is much longer than the right side

What is the direction of a distribution’s skewedness toward?

the long tail

When is the distribution of a quantitative variable unimodal?

if it has a single peak

When is the distribution of a quantitative variable bimodal?

if it has two distinct clusters and peaks

When is the distribution of a quantitative variable approximately symmetric?

if the frequencies are about the same for all values

What do we look for in any graph?

the overall pattern and any clear departures from that pattern

How do we describe the overall pattern of a distribution?

by its:

• shape

• center

• variability

What do we call an important kind of departure from the overall pattern of a distribution?

outlier

What is it important to remember when comparing distributions?

to give context and use comparative language

How do you make a stemplot?

1. Separate each observation into a stem (all but the final digit) and a leaf (the final digit)

2. Write the stems in a vertical column with the smallest at the top. Draw a vertical line to the right of the column

3. Write each leaf in the row to the right of the stem

4. Arrange the leaves in increasing order out of the stem

5. Provide a key that identifies the variable and explains what the stems and leaves represent

How can we get a better picture of a distribution with “bunched up” data values?

by splitting stems

How can we compare two distributions of the same quantitative variable?

by using a back-to-back stem plot

How does a histrogram display data?

it shows each interval of values as a bar, with the heights of the bars showing the frequencies or relative frequencies of values in each interval

How do you make a histogram?

1. Choose equal-width intervals that span the data

2. Make a table that shows the frequency or relative frequency of individuals in each interval

3. Draw horizontal and vertical axes. Label the axes

4. Scale the axes

5. Draw bars above the intervals. The bar heights correspond to the frequency or relative frequency of individuals in that interval

What is the most common measure of center?

mean

How do you find the mean?

by adding all values in a set of observations and then dividing that sum by the number of observations

What is the median of a distribution?

the center

What does the symbol x̄ represent?

the mean of a sample

What does the symbol μ represent?

the mean of a population

What is a statistic?

a number that describes some characteristic of a sample

What is a parameter?

a number that describes some characteristic of a sample

When is a statistical measure resistant?

if it isn’t sensitive to extreme values

How do you find the median of a distrbution?

1. Arrange all observations from smallest to largest

2. If the number of observations n is odd, the median is the middle obesrvation in the ordered list

3. If the number of observations n is even, the median is the average of the two center observations in the ordered list

When are the mean and median of a distribution similar?

if the distribution is roughly symmetric and has no outliers

How does the skewedness of a distrbution’affects its mean and median?

if the distribution is strongly skewed, the mean will be pulled in the direction of skewedness but the median won’t

How do the mean and median react to outliers?

the median is resistant to outliers but the mean isn’t

What is the range of a distribution?

the distance between the minimum value and the maximum value

Is range a resistant measure of variability?

no

What does standard deviation measure?

the typical distance of the values in a distribution from the mean

How do you calculate standard deviation?

1. Find the mean of the distribution

2. Calculate the deviation of each value from the mean

3. Square each of the deviations

4. Add all the squared deviations, divide by n-1

5. This is the sample variance

6. Take the square root

What is the formula for standard deviation?

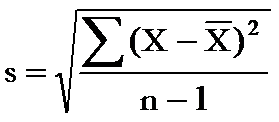
What is the standard variance?

standard deviation before you square root it

What is standard deviation always greater than or equal to?

0

What do larger values of standard deviation indicate?

greater variation

Is standard deviation a resistant measure of variability?

no

What do the quartiles of a distribution do?

divide the ordered data set into four groups having roughly the same number of values

How do you find the quartiles of a distribution?

arrange the data values from smallest to greatest and find the median

What is the first quartile Q₁ of a distribution?

the median of the data values that are to the left of the median in the ordered list

What is the third quartile Q₃ of a distribution?

the median of the data values that are to the right of the median in the ordered list

What is the interquartile range (IQR)?

the distance between the first and third quartiles of a distribution

IQR = Q₃ - Q₁

What is the rule for outliers?

an observation is an outlier if it falls 1.5 x IQR above the third quartile or below the first quartile

low outliers < Q₁ - 1.5 x IQR | high outliers < Q₃ + 1.5 x IQR

Why do we look for outliers?

• they might be inaccurate data values

• they can indicate a remarkable occurrence

• they can heavily influence the values of some summary statistics, like the mean, range, and standard deviation

What does the five-number summary of a distribution consist of?

the minimum, the first quartile Q₁, the median, the third quartile Q₃, and the maximum

What is a boxplot?

a visual representation of the five number summary

How do you make a boxplot?

1. Find the five-number summary

2. Identify the outliers using the 1.5 x IQR rule

3. Draw and label the horizontal axis

4. Scale the axis

5. Draw a box (from the first quartile to the third quartile)

6. Mark the median

7. Draw whiskers (to the minimum and the maximum)

8. Outliers are marked with a special symbol such as an asterisk

What is percentile used to do?

to describe the location of a value in a distribution

How do you find the percentile of a value?

count the number of values less than or equal to it, then divide by the total number of values

What is a cumulative relative frequency graph?

a graph that plots a point corresponding to the percentile of a given value in a distribution of quantitative data and connects consecutive points using line segments

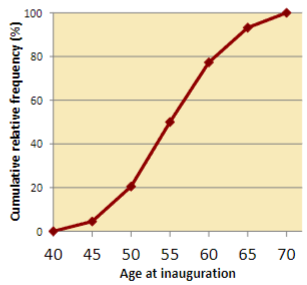
cumulative relative frequency graph

What does a z-score tell us?

how many standard deviations from the mean an observation falls and in what direction

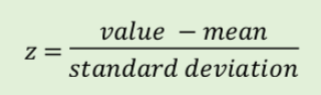
formula for z-score

What is a standardized score often called?

z-score

What does transforming data do?

• converts the original observations from the original units of measurement to another standardized scale

• can affect the shape, center, and variability of a distribution

What are the effects of adding/subtracting a constant to/from a distribution?

adding/subtracting the same positive number a to/from each observation:

• adds/subtracts a to/from measures of center and location (mean, five-number summaries, percentile)

• does not change measures of variability (range, IQR, standard deviation)

• does not change the shape

What are the effects of multiplying/dividing a constant by the distribution?

multiplying/dividing each observation by the same positive number b:

• multiplies/divides measures of center and location (mean, five number summaries, percentiles) by b

• multiplies/divides measures of variability (range, IQR. standard deviation) by b

• does not change the shape

What is a density curve?

a curve that

• is always on or above the horizontal axis

• has an area of exactly 1 underneath it

What does a density curve describe?

the overall pattern of a distribution

What does the area under the density curve and above any interval of values on the horizontal axis estimate?

the proportion of all observations that fall in that interval

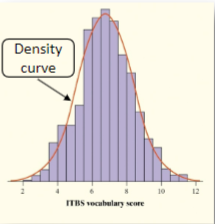
density curve

What is the mean of a density curve?

the point at which the curve would balance if made of solid material

What is the median of a density curve?

the equal-areas point, the point that divides the area under the curve in half

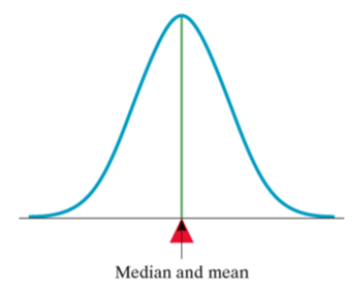
mean and median of a symmetric curve

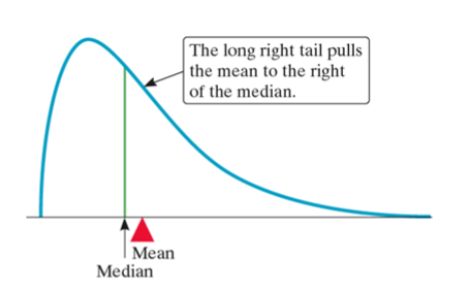
mean and median of a right skewed curve

What is a density curve an idealized description of?

a distribution of data