Ap calc Vocab

Twice differentiable

if you can differentiate its firs derivative

Fundamental Theorem of Calculus

states that differentiation and integration are inverse operations.

Mean Value Theorem

if a function f is continuous on the closed interval [a,b], and differentiable on the open interval (a,b), then there exists a point c in the open interval (a,b) such that

Mean Value Theorm of Integrals

there exists a point c in the interval [a,b] where the function has the same average value as its definite integral over the interval.

Extreme Value Theorem

If f is continuous on a closed interval [a,b], the f attains an absolute maximum value f(c) and an absolute minimum value at some numbers c and d in [a,b].

intermediate value theorem

if you draw a continuous curve on a graph between two points, it must cross every y-value in between at least once.

absolute minimum

the lowest point of a function

absolute maximim

the highest point of a function

absolute value

the distance between a number and the origin

acceleration

the rate of change of velocity over time

Separation of variables

ex: dx/dy=yx ,, xdx=y/dy

even function

Symmetric with respect to the y axis

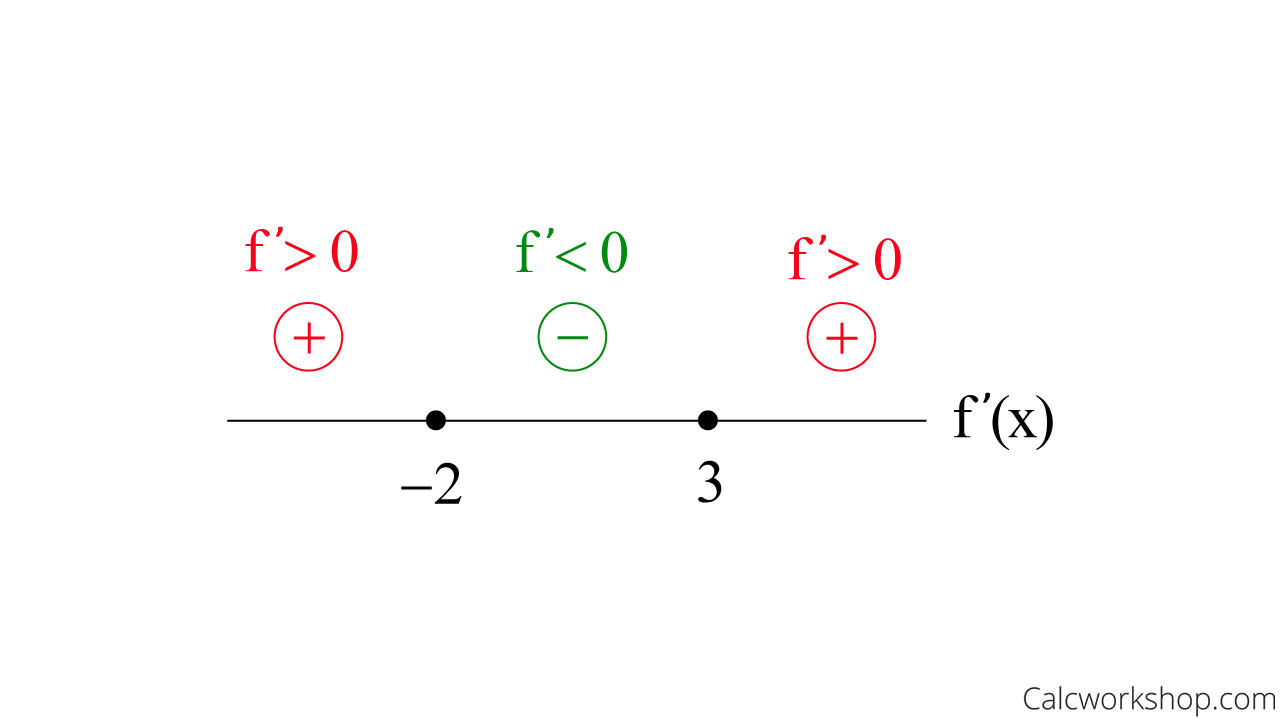
first derivatve test

Determines whether a point is minimum, maximum, or neither

inflection point

where the function changes from concave up to concave down or vice versa

instantaneous rate of change

the rate of change(value of the derivative) at a particular moment

inverse funcition

a function obatined by switching the x and y variables in a function

l'hopital's rule

Finding the derivative of the numerator and denominator to evaluate the limit of a function.

local extrema

a point where the graph has a peak or a valley

second derivative test

determines whether the function is concave down, up, of neither at a point.

Suppose f" is continuous near c. \n a) if f'(c)=0 and f"(c)>0 then f has a local minimum at c \n b) if f"=0 and f"(c)<0 then f has a local maximum at c