Fault Tolerance

Hardware Redundancy

addition of extra hardware, usually for the purpose of detecting and tolerating faults

Software Redundancy

addition of extra software beyond what is needed to perform a given function, to detect and possibly tolerate faults.

Information Redundancy

addition of extra information beyond that is required to implement a given function, for example error detecting codes.

Time Redundancy

uses additional time to perform the functions of a system such that fault detection and often fault-tolerance can be achieved.

Hardware Redundancy DISADVANTAGE/Solution

higher production cost

using time redundancy to preform the task

better suited for non-time-critical applications

Transient Fault Detection:

Perform same computation 2 or more times (2 times: fault detection; 3 or more times: fault correction by majority vote)

Permanent Fault Detection:

Calculating everything twice will not help, so instead 1) calculate normal result, 2) repeat calculation with encoded data (e.g. complement, arithmetic shift, etc.

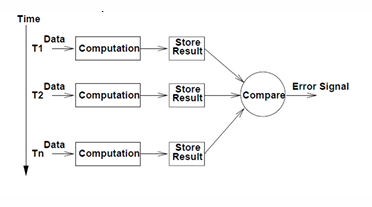
Time Redundancy - Transient Fault Detection

computations are repeated at different points in time and then compared. No extra hardware is required

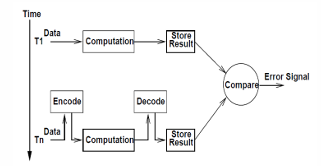
Time Redundancy - Permanent Fault Detection

During first computation, the operands are used as presented. • During second computation, the operands are encoded in some fashion. • The selection of encoding function is made so as to allow faults in the hardware to be detected.

3 basic forms of hardware redundancy:

passive (static) techniques

active (dynamic) techniques

hybrid techniques

Passive (static) techniques

use fault masking to hide the occurrence of faults and prevent the faults from resulting in errors.

Active (dynamic) techniques

achieve fault tolerance by detecting the existence of faults and performing some actions to remove the faulty hardware.

Hybrid techniques

ombine attractive features of both passive and active techniques. Fault masking is used in hybrid systems to prevent erroneous results from being generated. Fault detection, location and recovery are also used to improve fault tolerance by removing faulty hardware.-

often used in critical applications-

very expensive form of redundancy scheme to implemen

N-Modular Redundancy (NMR)

N must be odd and can tolerate the upper bound of N/2

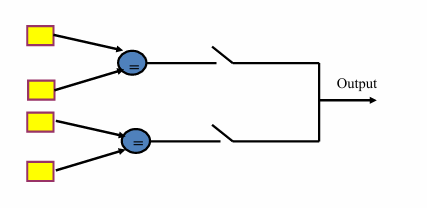
Pair-and-a-Spare Technique

combines the features present in both standby sparing and duplication with comparison

Two modules are operated in parallel at all times and their results are compared to provide the error detection capability required in the standby sparing approach .

Second duplicate (pair, and possibly more in case of pair and k spare) is used to take over in case the working duplicate (pair) detects an error.

A pair is always operational

INFORMATION REDUNDANCY

Adding extra information beyond that is required to implement a function (i.e. addition of extra information to data words)

Coding

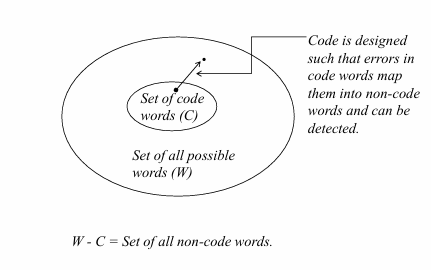
Set of all non-code words.

W - C w= set of all possible words. c set of code words

Bit Error:

A single bit of information is corrupted from 1 to 0 or from 0 to 1

Symmetric Errors:

0→1 and 1 → 0 errors are equally likely to occur

Asymmetric Errors:

A given word has only 0 → 1 OR 1 → 0 errors, and it is known a priori which type exists.

Unidirectional Errors

A given word has only 0 → 1 OR 1 → 0 errors, but it is not known a priori which type exists

Byte Errors

Errors will affect bytes independently, but it is not known how many bits are affected or the type of effect

Burst Errors

cluster of K consecutive bits are in error

Code / Hamming Distance

how much they differ in position

0011 and 0101 have a hamming distance of 2

hamming distance value 1

then it is possible to change one into another by magnifying one bit in one of the words. However, if 2 words differ in 2 bit positions, it is impossible to transform one word to another by changing 1 bit in one of the words

code distance

as the minimum Hamming distance between any two valid code words

Error detecting codes (EDC) To detect d errors

the code words must have code distance of at least d+1

Error correcting codes (ECC) To correct c errors

the code words must have code distance of at least 2c+1

a code can correct up to c bit errors and simultaneously detect up to d additional bit errors if and only if

Hd ≥ 2c + d + 1

A separable code

is one which, original information is appended with new information to form code words

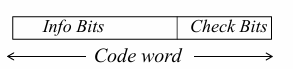
A non-separable code

does not posses the property of separability, i.e, not partitioned directly into info and check bits => complicated decoding procedure!

m-out-of-n codes

n bits in total; m # 1’s and (n-m) # 0’s

Advantages of m-out-of-n codes

conceptually simple • easy to visualize error detection process

Disadvantages - m -out of -n

encoding, decoding and detection processes are often difficult to perfor

Berger Codes (separable codes)

are formed by appending a special set of bits (check bits) to each word of information. Hence, they are separable codes

arithmetic code error corection

can correct up to c errors if and only if the arithmetic distance is ≥ 2c + 1

Residue Codes

a seperable srithmitic code formed by appending the residue of a number to that number

ie D|R where D is the original data and R is the residue to the og data

Inverse-Residue Codes

Rather than appending the residue, the inverse residue is calculated and appended.

weight of a code word

the number of 1s in a word

Reflexivity

Hd (x, y) = 0 if and only if x = y.

symmetry

Hd (x, y) = Hd (y, x).

Triangle inequality:

Hd (x, y) + Hd (y, z) ≥ Hd (x, z).

Odd Parity:

Total # 1’s in the code word is odd

even Parity:

Total # 1’s in the code word is even

(n,k) codes

a code of length n (# of columns in the matrix) will have 2^k code words k = (n - rows)

If H has a column of all zeros

Hd = 1

if H has 2 collums that are the same

Hd=2

if no columns are all 0 and all distinct

Hd>=3, if 3 columns are LD (add up to 0) then the Hd = 3

N(x,y)

number of 1 → 0 changes we have when we go from x to y

N(x,y) + N(y,x) =

Hd(x,y)

For a code to detect all unidirectional errors, it must have

min N(x,y) >= 1 min Hd (x,y) >= 2

For a code to correct c symmetric errors plus detect all unidirectional errors, we must have:

Min N(x,y) >= c +1 Hd(x,y) >= 2(c+1)

Berger Codes (separable codes

formed by appending a special set of bits (check bits) to each word of information. Hence, they are separable codes.

advantages of berger codes

separable code

can detect multiple uni directional errors

use fewest number of check bits of all seperable codes

UED codes

unidirectional error detection

SEC - UED code

requires 2log(base 2) K

arithmetic codes correction

can correct c erroes if Hd >= 2c+1

arithmetic code detection

can only detect d errors i Hd >= C+ d + 1

arithmetic code

An ____ code A has the property that A(x op y) = A(x) op A(y), where x and y are operands, op is some arithmetic operation, and A(x) and A(y) are arithmetic codes for x and y, respectively.

Residue Codes

a ___ code is a separable arithmetic code formed by appending the residue of a number to that number

cyclic codes

a parity check code which has the additional property that every cyclic shift of a code word is also a code word

m out of n codes, number of code words for length n and number of 1s m

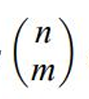
m out of n codes, best codes of this type for length n and number of 1s m

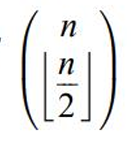
berger codes, number of check bits given K INFO bits

upper bound of log base 2(k+1)

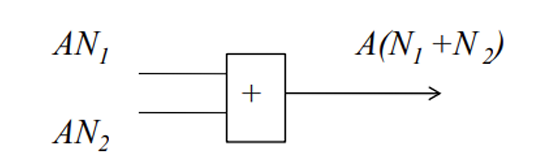
AN Codes

simplest arithamtic codes, formed by multiplying each data word N by some constant A

D(X) Non-Systematic Cyclic Encoding: given d = [1110]

starting with X^0—> X^n where n is the length of d add the vaues of d to the X^i

D(x) = X²+X+1

The generator polynomial has the following properties:

degree of G(x) = n - k

G(x) is the unique lowest-degree nonzero polynomial having unity coefficient in its highest-degree term

each code word V(x) is a multiple of G(x) and is computed as V(x) = D(x) G(x

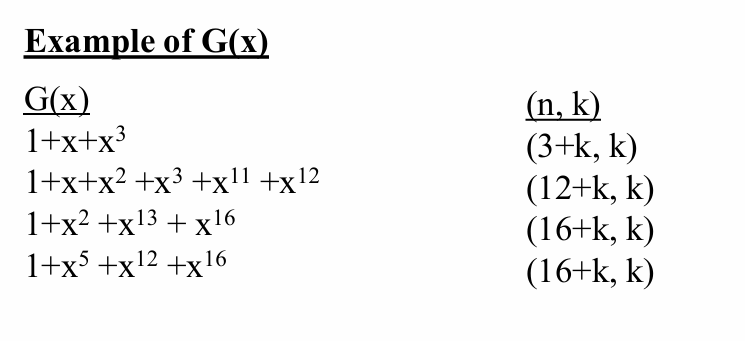
For t malfunction diagnosis:

>= 2t + 1 units

each unit in t-diagnosable systems must be tested by

>= t other units

Fail silent model

when a processor becomes faulty, it will produce known, fixed outputs (deterministic fault)

Byzantine fault model-

when a processor becomes faulty, it will produce unpredictable (and possibly malicious) outputs (non deterministic fault

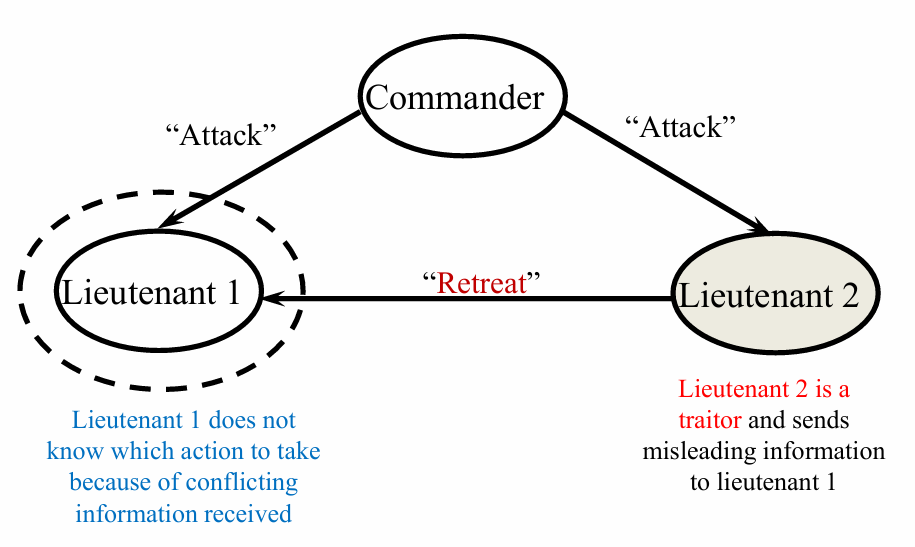
Byzantine General’s Problem

m is a model of computer failure that allows for malicious behavior, A failed computer can send conflicting information to different parts of a system causing operational components to make incorrect decisions.

Two conditions must be satisfied: Byzantine General’s Problem

A commanding general must send an order to its n-1

lieutenants such that:

IC1 -- all loyal (fault-free) lieutenants obey the same order–

IC2 -- if the commanding general is loyal then every loyal lieutenant obeys the order from the commanding general

The Byzantine General’s problem is modeled after a military analogy.

Several divisions of an army are camped outside enemy lines.Each division is commanded by a general. the generals can either send or recive an ATTACK or RETRITE message, one more more gernals can be traitors, in order to reach an agreement 2/3 of the generals must be loyal

Byzantine Requirements

tolerate up to M faults

at least 3m+1fault contaiment regions (generals)

at least 2m+1 disjoint connectivity (communication paths)

inputs must be changed at least m+1 times (rounds of communication)