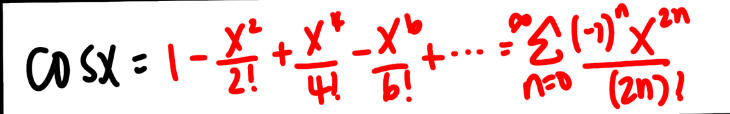AP Calculus BC Review

horizontal asymptote

limit as x approaches infinity equals a constant 'a', y=a.

vertical asymptote

limit as x approaches 'b' equals infinity, x=b

Continuity Conditions

lim x→c f(x) exists, f(c) exists, and lim x→c f(x) = f(c)

Jump Discontinuity

lim x→c f(x) DNE

Hole/Removable Discontinuity

lim x→c f(x) ≠ f(c)

Infinite Discontinuity

f(c) DNE

Intermediate Value Theorem

if f is continuous on [a, b] and K is a number between f(a) and f(b), then there exists c in [a, b] such that f(c) = K.

Squeeze Theorem

If h(x) <= f(x) <= g(x) for all x near c, and lim x→c h(x) = lim x→c g(x) = L, then lim x→c f(x) = L

Instantaneous Rate of Change

tangent line

f’(x) = lim h→0 [f(x+h)-f(x)/h]

or, at a point c:

f’(c) = lim x→c [f(x)-f(c)/x-c]

Average Rate of Change

secant line

f(b) -f(a)/b-a

Non-differentiable points

Cusp, sharp turn, vertical tangent.

Derivative of a^x

(ln|a|)a^x

Derivative of log_ax

1/x*ln|a|

Chain Rule

f'(g(x)) * g'(x)

Equation of a Tangent Line

y - f(c) = f’(c)(x-c)

Derivative of an Inverse Function

d/dx[f^-1(x)] = 1/f’(f^-1(x))

Speed

|v(t)|

Interpretation of Sign of Velocity Function

v = 0 → particle at rest

v > 0 → moving right/up

v < 0 → moving left/down

Interpretation of Sign of Acceleration Function

a = 0 → constant velocity

a > 0 → accelerating to the right/up

a < 0 → accelerating to the left/down

speeding up

v(t) and a(t) are same sign

slowing down

v(t) and a(t) are opposite signs

1st Derivative Test

1) find critical points (f’(x) = 0)

2) make sign chart

3) if f’(x) changes from + to -, f(x) has a relative max.; if f’(x) changes from - to +, f(x) has a rel. min.; if it doesn’t change, neither

2nd Derivative Test

1) find critical points (f’(x) = 0)

2) if f’’(c) < 0, concave down; f(c) is a rel. max.; if f’’(c) > 0, concave up; f(c) is a rel. min; if f’’(c) = 0, test is inconclusive.

If f' is positive, f(x) is

Increasing

If f' is negative, f(x) is

decreasing

If f'' is positive, f(x) is

concave up

If f’’ is negative, f(x) is

concave down

Point of Inflection

f’’(x) = 0 AND f’’(x) changes sign

Relative Maximium/Minimum

critical point where f’(x) changes sign

EVT

if f(x) is cont. on [a,b], then f(x) has a max and min on the interval

MVT

if f(x) is cont. on [a,b] and differentiable on (a,b), then there exists a number c on the interval such that: f'(c)= (f(b)-f(a))/(b-a)

IROC = AROC

slope of tangent line = slope of secant line

Finding Absolute Extrema

1) Find critical points

2) Plug in critical points into original function

3) Plug in endpoints of interval into original functoin

4) highest y-value → max, lowest y-value → min

Fundamental Theorem of Calculus (FTC)

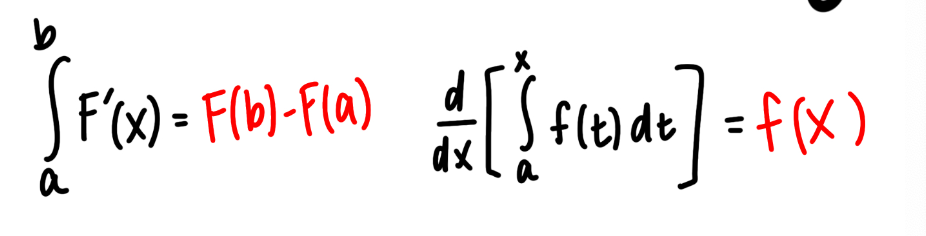
tan^-1(x) special integral formula

1/a arctan(x/a) + C

(a is a constant)

IBP Formula

int(udv) = uv - int(vdu)

Order for IBP Selection

Log

Inverse Trig

Algebraic

Trig

Exponential

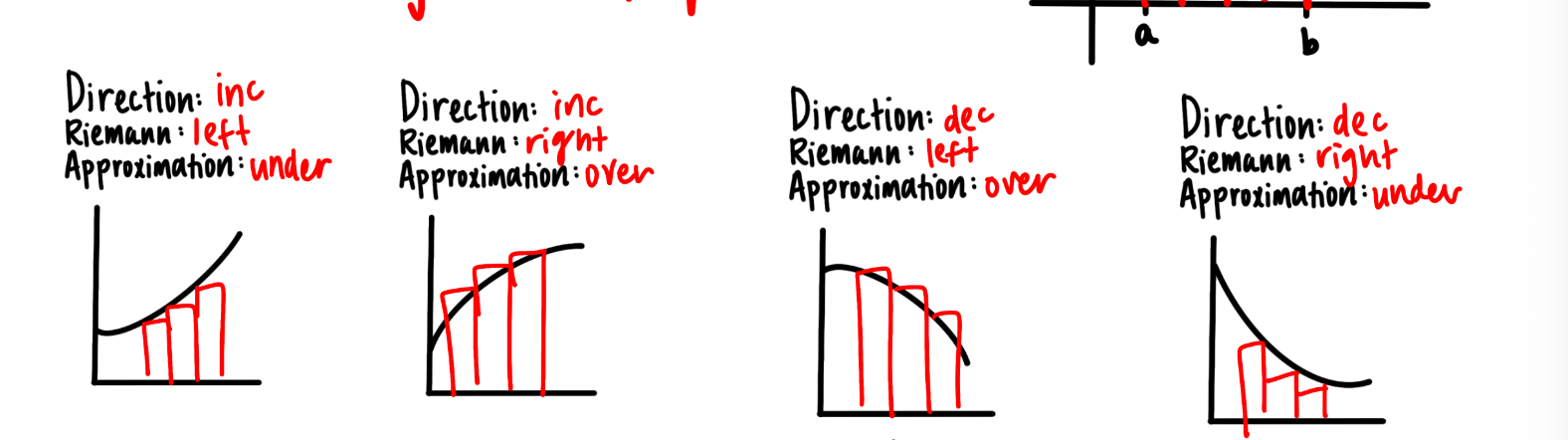
Riemann Sum Formulas

Rectangular Riemann Sum Approximation Errors

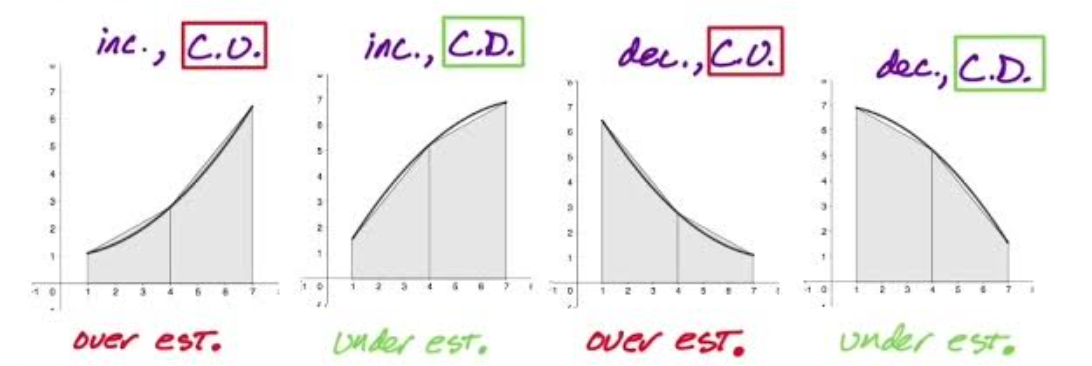
Trapezoidal Riemann Sum Approximation Error

If the function is concave up, the Riemann sum will be an overestimate. If the function is concave down, the Riemann sum will be an understand.

Midpoint Riemann Sum Approximation Error

If the function is concave up, the midpoint Riemann sum will be an underestimate. If the function is concave down, the midpoint Riemann sum will be an overestimate

(opposite of trapezoid)

Exponential Growth/Decay

dy/dt = ky → y = Ce^kt

Logistic Growth

dy/dt = ky(1 - y/L) → y = L/1+be^-kt (look juan (1) be a kitty (k-t))

L = carrying capacity

inflection point at L/2, growth rate is max. at this value

Euler's Method

initial: (x₀, y₀)

h: value of each step (total distance/# of steps)

F(x,y): differential equation (may be off a diff. form)

x_n = x_n-1 + h

y_n = y_n-1 + h*(F(x_n-1, y_n-1))

Avergge Value of a Function

1/b-a * int(a, b, f(x))

Area Between Two Curves

int(a, b, f(x) - g(x)) where f(x) is upper function

int(a, b, f(y) - g(y)) where f(y) is right-most function

Average Veolcotiy

1/b-a * int(a, b, v(t))

Total Distance Traveled

int(a, b, |v(t)|)

Displacement (from a point)

s(0) + int(a, b, v(t))

Volume (Cross-Sections)

int(a, b, Area)

base of shape sitting perp. to x-axis (top-bottom) or y-axis (right-left)

Disc Method

V = π * int(a, b, [f(x)]²)

over a line: π * int(a, b, [f(x) - k]²)

Washer Method

V = π * int(a, b, [[f(x)]²-[g(x)]²]]) where f(x) is outer function

over a line: π * int(a, b, [[f(x)-k]²-[g(x)-k]²]])

Arc Length of a Curve

int(a, b, sqrt(1 + [f’(x)]²))

Parametric Derivatives

dy/dx = (dy/dt) / (dx/dt)

d²y/dx² = d/dt(dy/dx)/dx/dt

Parametric Tangents

horizontal tangent: dy/dt = 0

vertical tangent: dx/dt = 0

Arc Length of a Parametric Curve

int(a, b, sqrt([dx/dt]²+[dy/dt]²))

Speed (Vector)

sqrt([dx/dt]²+[dy/dt]²)

same as arc length (without the integral)

Distance Traveled (of a vector)

int(a, b, sqrt([dx/dt]²+[dy/dt]²))

same as arc length/speed

Vector Position Formula

x(t₂) = x(t₁) + int(t₁, t₂, dx/dt)

y(t₂) = y(t₁) + int(t₁ + t₂, dy/dt)

Derivative of a Polar Function

dy/dx = f’(θ)sinθ + f(θ)cosθ / f’(θ)cosθ - f’(θ)sinθ

Polar Conversions

(x,y) → (r,θ)

r = sqrt(x² + y²)

tan^-1(y/x) = θ

(r, θ) → (x,y)

x = rcosθ

y = rsinθ

Area of a Polar Curve (Singular)

½ * int(a, b, r²dθ)

Area Between Two Polar Curves

½ * int(a, b, [[f(θ)]² - [g(θ)]²]); where f(θ) is outer polar curve

Arc Length (Polar Curve)

int(a, b, sqrt(r²+(dr/dθ)²))

nth term test

if lim n→ ∞ a_n ≠ 0, series diverges

CONVERSE IS NOT NECESSARILY TRUE

Geometric series

Σa₁(r)^n-1

if |r| < 1, converges

if |r| ≥ 1, diverges

Sum of a Convergent Geometric Series

a₁ / 1 - r

p-series

Σa_n = Σ1/n^p

if p > 1: converges

if p ≤ 1: diverges

Direct Comparison Test

if a_n ≤ b_n OR a_n > b_n for all n,

if one converges/diverges, so does the other.

Limit Comparison Test

if lim n → ∞ [a_n/b_n] = finite/positive (L ≠ 0 or ±∞):

a_n and b_n either both converge or diverge.

Alternating Series Test

if lim n→∞ a_n = 0 AND a_n is decreasing, series is convergent.

Alternating Series Estimation Theorem

|R_n| = |S - S_n| ≤ b_n+1

Remainder (error) of estimation using a finite partial sum is no greater than value of following term.

Integral Test

if f(x) is cont., positive, and decreasing:

if int(f(x)) converges, series converges; if int(f(x)) diverges, series diverges.

Ratio Test

lim n→∞ |a_n+1 / a_n| = L

if L < 1: converges

if L > 1: diverges

if L = 1: inconclusive

Telescoping Series

1/n(n+1); a series where most terms cancel each other out, leading to a simple sum of the remaining terms (convergent)

Harmonic Series

1/n; divergent

Absolute Convergence

A series is said to converge absolutely if the series of its absolute values converges. This implies that the original series also converges.

Conditional Convergence

A series converges conditionally if it converges, but its series of absolute values diverges. This means that the convergence of the series relies on the specific arrangement of its terms.

Taylor Polynomial

f(c)+ f'(c)(x-c) + f’’(c)(x-c)^2/2! + f'''(c)(x-c)^3/3! + …

Maclaurin Polynomial

f(0)+ f'(0)(x) + f’’(0)(x)^2/2! + f'''(0)(x)^3/3! + …

Finding Interval of Convergence

1) Use Ratio test to determine values of x that makes the series converge (lim n→ ∞ |a_n+1/a_n|) < 1)

2) check endpoints by plugging into original function (plug in for x; if series converges, inclusive; if series diverges, exclusive)

1/1+x Power Series

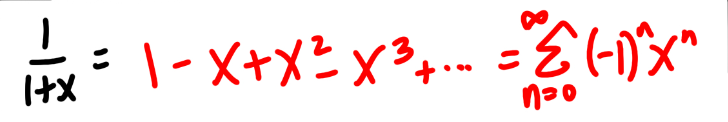
e^x Power Series

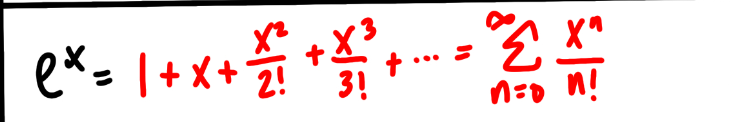
sin x Power Series

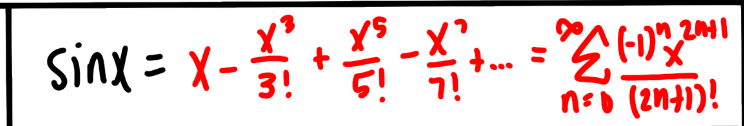
cos x Power Series